MIT线性代数公开课精讲：四大子空间与高斯消元

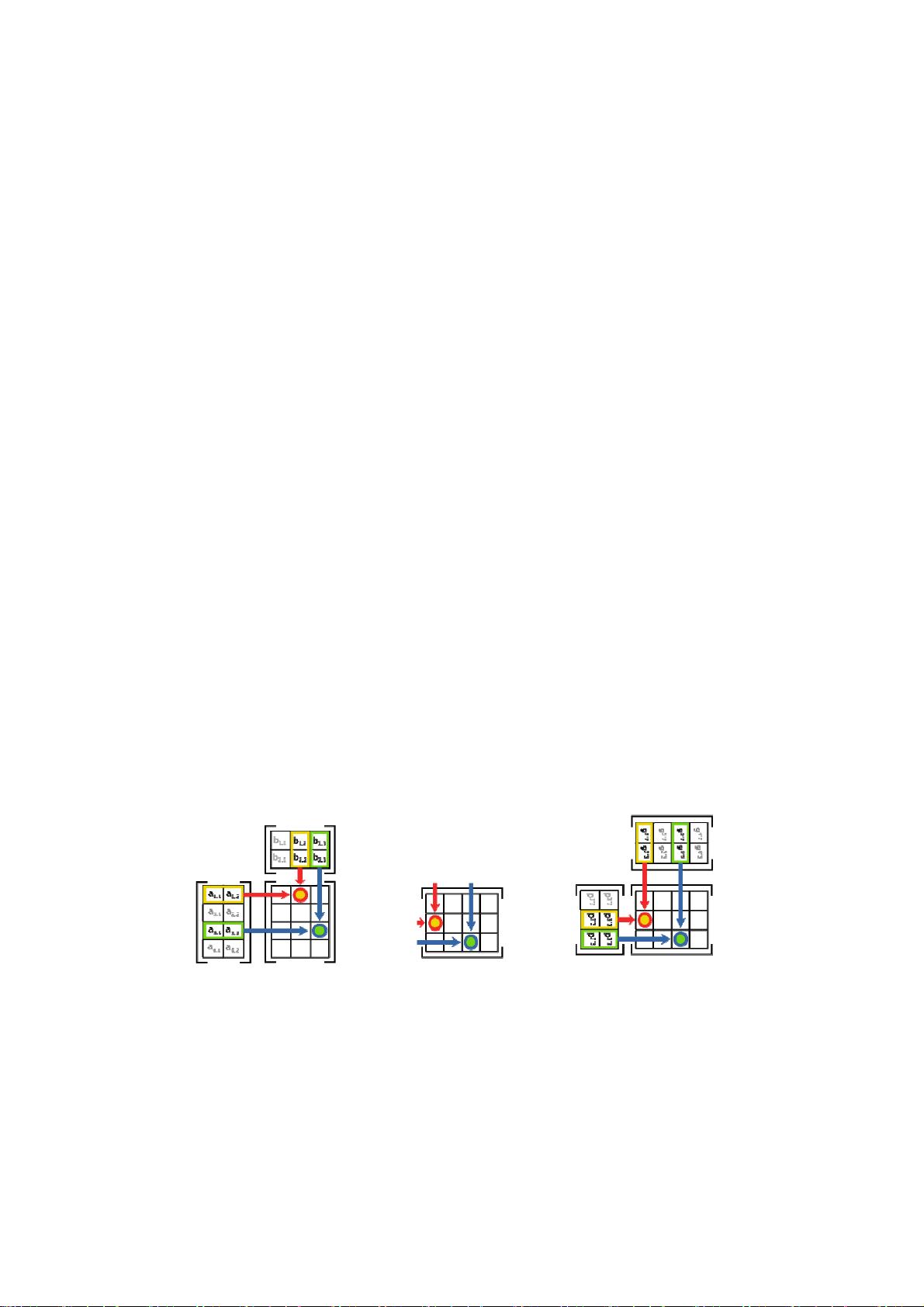
"这篇笔记详细记录了麻省理工大学(MIT)18.06线性代数公开课的内容，包括34讲的详细笔记，涵盖了线性方程组、矩阵理论、线性空间等多个主题。" 线性代数是数学的一个核心分支，特别是在理工科学习中占有举足轻重的地位。MIT的18.06线性代数公开课是学习这一领域的宝贵资源，由著名教授Gilbert Strang讲授。课程分为多个单元，首先从解决线性方程组(Ax=b)出发，引导学生理解线性代数的基本概念。 第一单元主要讲解了线性方程组的解法，包括高斯消元法，这是解决线性问题的基础。矩阵的乘法、逆矩阵、LU分解等都是这一部分的重点。矩阵的LU分解是数值线性代数中的一种重要技巧，可以高效地求解线性方程组。 接着，课程深入到矩阵的性质，如转置、置换和空间的概念，这些是理解线性变换的基础。列空间和零空间的概念被引出，它们是线性方程组解的几何表示。求解Ax=0时，主变量和特解的概念帮助我们理解线性系统的解结构。 线性相关性和基的概念是线性代数中的基石。它们定义了向量空间的维度，并且解释了为什么某些线性方程组有唯一解，有些则有无限多解。四个基本子空间，包括列空间、零空间、行空间和对偶空间，是理解线性系统和矩阵运算的关键。 此外，课程还涉及矩阵空间、秩1矩阵以及它们在图论和网络分析中的应用。复习章节则帮助巩固前面的知识，确保学生能扎实掌握线性代数的基本思想和工具。 传统的线性代数教材往往从行列式开始，但Strang教授的现代教学方法强调了线性方程组和线性空间的重要性。他通过列图像来引入线性相关性的理解，突出了矩阵运算中对行和列的独立操作，这种方法更加直观，有助于学生更好地掌握线性代数的实际应用。 这门课程深入浅出地介绍了线性代数的核心概念，不仅提供了理论知识，还涵盖了实际问题的解决策略，是理工科学习者不可多得的学习资料。通过这34讲的笔记，学生可以系统地回顾和巩固课程内容，进一步提升自己在线性代数领域的理解和应用能力。