没有合适的资源?快使用搜索试试~ 我知道了~
首页蒙特卡洛方法与MCNP教程
资源详情
资源评论
资源推荐

蒙特卡罗方法与 MCNP 程序入门
目 录
第1章 蒙特卡罗方法简介.....................................................................................................................................1
§1.1 蒙特卡罗方法的基本原理.................................................................................................................1
§1.2 蒙特卡罗方法的解题手续和特点.........................................................................................................6
§1.3 用蒙特卡罗方法模拟粒子输运............................................................................................................7
第2章 MCNP程序入门..........................................................................................................................................9
§2.1 MCNP简介.............................................................................................................................................9
§2.2 MCNP程序的组成及特点...................................................................................................................11
§2.3 MCNP4C程序安装、运行与源程序编译...........................................................................................13
§2.4 MCNP输入文件...................................................................................................................................17
第3章 MCNP程序中的几何构建........................................................................................................................23
§3.1 基础知识..............................................................................................................................................23
§3.2 几何描述卡..........................................................................................................................................26
§3.3 有效地构建几何..................................................................................................................................30
第4章 MCNP程序的数理基础............................................................................................................................33
§4.1 物理......................................................................................................................................................33
§4.2 记数......................................................................................................................................................41
§4.3 减小方差技巧......................................................................................................................................48
第5章 MCNP程序中的数据卡............................................................................................................................57
§5.1 问题类型卡..........................................................................................................................................57
§5.2 栅元参数和曲面参数卡......................................................................................................................57
§5.3 源的描述..............................................................................................................................................67
§5.4 记数方式的指定..................................................................................................................................76
§5.5 材料的指定..........................................................................................................................................90
§5.6 能量和热处理方式的指定..................................................................................................................92
§5.7 问题截断条件......................................................................................................................................96
§5.8 外围卡..................................................................................................................................................97
§5.9 MCNP输入文件综述.........................................................................................................................100
第6章 经验.........................................................................................................................................................104
§6.1 一般应用步骤....................................................................................................................................104
§6.2 需注意的问题....................................................................................................................................104
第7章 应用实例.................................................................................................................................................106
§7.1 医学物理中的应用............................................................................................................................106
§7.2 反应堆物理计算中的应用................................................................................................................132
附 录...................................................................................................................................................................161
连续能量中子截面库ENDL851数据目录................................................................................................161
中子热截面库BMCC1数据目录...............................................................................................................162
离散中子截面库D91数据目录..................................................................................................................163
光子截面库MCPLIB1数据目录................................................................................................................164
特殊材料S(,)热截面库TMCC1数据目录...........................................................................................165
参考文献............................................................................................................................................................168
- i -

蒙特卡罗方法与 MCNP 程序入门
第1章 蒙特卡罗方法简介
蒙特卡罗方法,又称随机抽样方法,是一种与一般数值计算方法有本质区别的计算方法
属于试验数学的一个分支,起源于早期的用几率近似概率的数学思想,它利用随机数进行统
计试验,以求得的统计特征值如均值、概率等作为待解问题的数值解。 随着现代计算机
技术的飞速发展,蒙特卡罗方法已经在原子弹工程的科学研究中发挥了极其重要的作用,并
正在日益广泛地应用于物理工程的各个方面,如气体放电中的粒子输运过程等。
§1.1 蒙特卡罗方法的基本原理
就数学特性而言蒙特卡罗方法的发展可以追溯到世纪著名的蒲丰问题。 年,
法国科学家蒲丰提出用投针试验计算圆周率值的问题。 这里我们用蒲丰问题来初
步说明蒙特卡罗方法的基本原理和解决问题的基本手续。
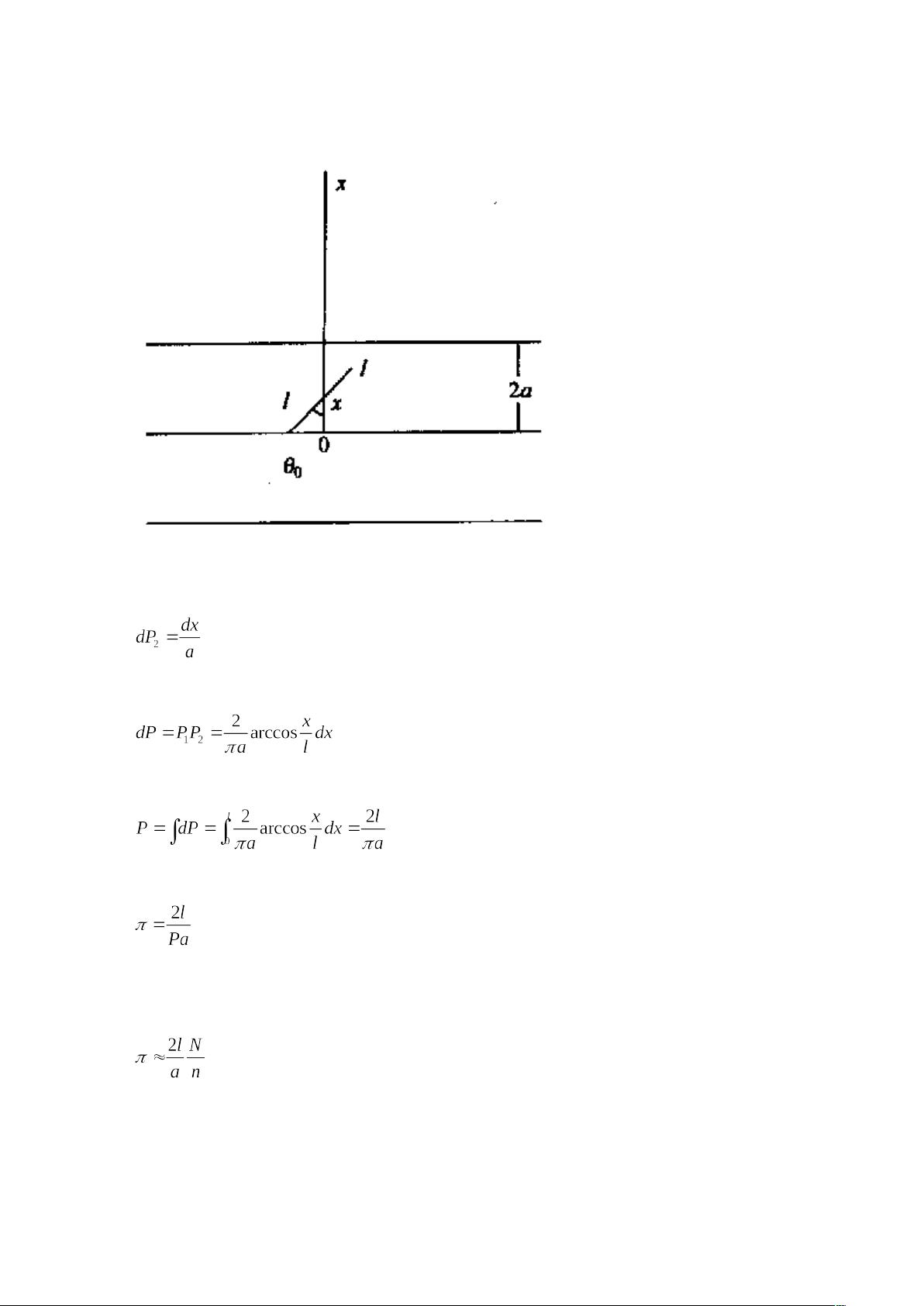
蒲丰问题是这样一个古典概率问题在平面上有彼此相距为的平行线,向此平面任意投一
长度为的针,假定,显然,所投的针至多可与一条直线相交, 那么,此针与任意条平
行线相交的概率可以求出,由下面的分析可知,此概率与所取针长、平行线间距有关,
并且包含有值。 在这里,任投一针的概率含义有以下三点针的中点
在平行线之间等
概率落入,即
距平行线的距离均匀分布在区间之内; 针与线的夹角均匀分布
在区间 之内;与互相独立。
如图所示,建立与平行线垂直且原点在某一条平行线上的轴,不失一般性,假定
针的中心处于图示中的轴上。由于对称性,我们只需分析针中心处在 范围的情况
即可。令探针中心的坐标值为显然,只有时才可能发生相交的事件。我们来分析在条
件满足时针与线相交的概率:
只有当 时才能相交,且相交的概率为
( )
- 1 -
蒙特卡罗方法与 MCNP 程序入门
下面再来分析针中心位置在轴上的分布显然这是一个均匀分布即针中心处于区间
内的概率为
()
这样,一次投掷,针中心落入且与线相交的概率为
()
则一次投掷,针与线相交的总概率为
()
即
()
从()式可见可利用投针试验计算值:设投针 次,其中次针与线相交,则可用频
率值! 作为概率"的估计值,从而求得的估计值为
(#)
这就是早期的用频率值作为概率近似值的方法的应用实例,表是在历史上一些有名的
用投针试验计算值的结果,其中针长以为单位。
表1.1 投针试验计算π值的结果
- 2 -
图 蒲丰问题的概率分
析
蒙特卡罗方法与 MCNP 程序入门
实验者
时间年份
针长 投针次数 相交次数 的估值
$% &#
'()*+ #
,- # #
. & &
/-00-1)) & &&
2-) & & & &
需要指出的是,上述由投针试验求得的近似值的方法,是进行真正的试验并统计试验
结果要使获得的频率值与概率值偏差小,就要进行大量的试验,这在实际中,往往难以做到
可以设想,对蒲丰问题这样一个简单的概率问题,若要进行万次投针试验,以每次投针、
作出是否相交判断并累加相交次数用时秒钟计算,则需用时万秒,即大约&个小时。
那么,可以设想,对于象上述确定条件下的核裂变、直流气体放电中粒子的输运过程及粒子
输运的总效应,若要用多次掷骰子的方法近似求出就是不可能的了。所以,在现代计算机技
术出现之前,用频率近似概率的方法——抑或称为雏形时代的蒙特卡罗方法——并没有得到
实质上的应用。
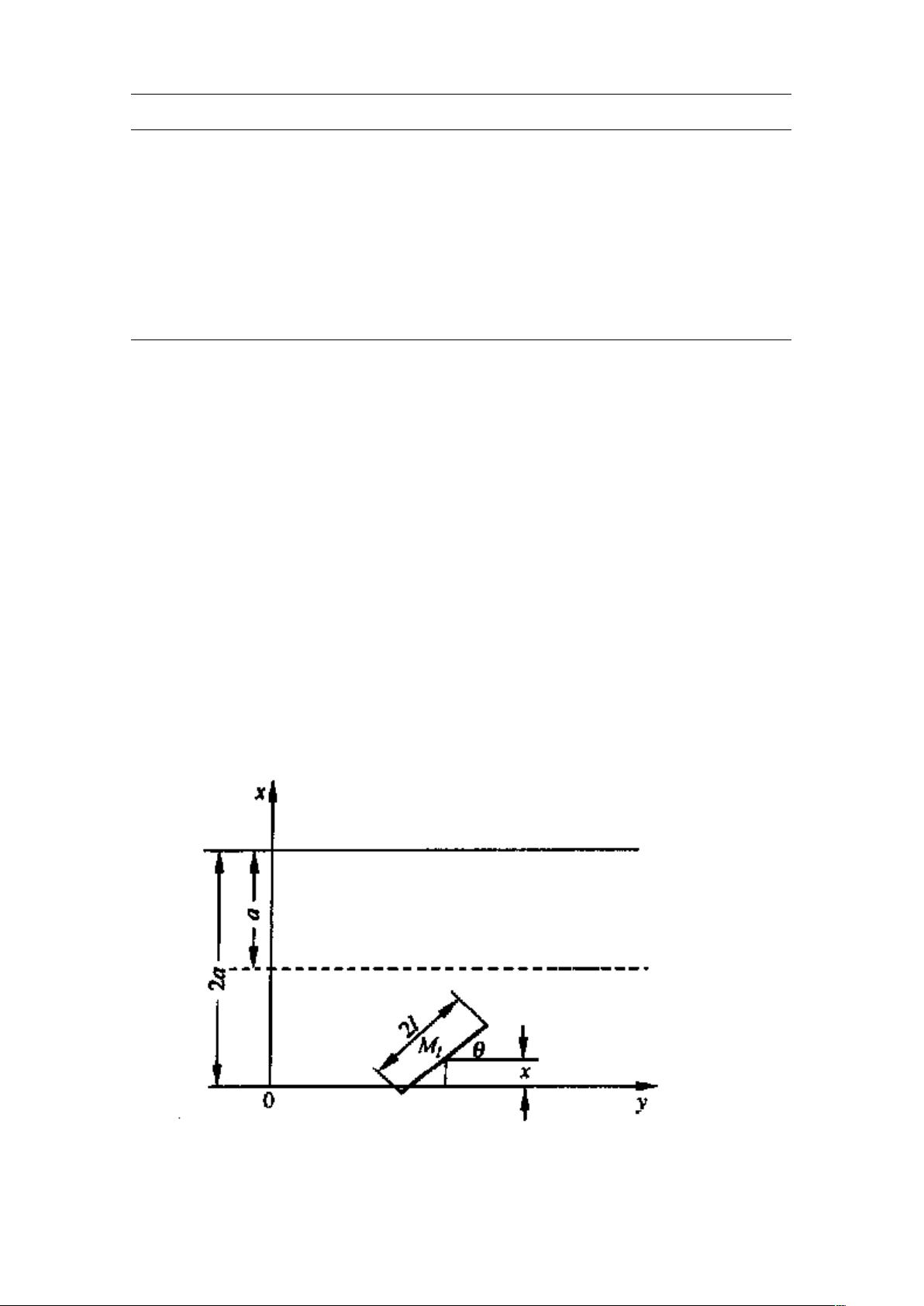
若用数值模拟方法代替上述的真正的投针试验,是利用均匀分布于之间的随机数
序列,并构造出随机投针的数学模型,然后进行大量的随机统计并求得的近似值。
如图建立坐标系,平面上一根针的位置可以用针中心
的坐标和针与平行线的夹角
来决定在3方向上的位置不影响相交性质。
- 3 -
图 用数值模拟方法计算蒲丰问
题

蒙特卡罗方法与 MCNP 程序入门
任意投针,意味着与都是任意取的。但的范围可限于的范围可限于。
在这种情况下针与平行线相交的数学条件是
()
其次,怎样模拟投针呢4亦即如何产生任意的。在任意取值,意味着在
上取哪一点的概率都一样,即的概率密度函数为
()
类似的,的概率密度函数为
(&)
由此,产生任意的过程就变为由%
1
抽样由%
2
抽样的过程。 容易得到
()
式中,5
1
,5
2
均为上均匀分布的随机数。只要随机数的均匀性和独立性良好如此构造
的数值模型就很好地模拟了实际试验中的一次投针并用下式判断是否相交且记录统计结果
如果投针 次,那么
()
是相交几率"的估计值。这样就实现了用数值方法模拟真正的投针试验。用此方法计算的的
近似值的情况如表所示。
表1.2 用蒙特卡罗方法计算的π的近似值
投针次数
的近似值
# && &
表中的计算结果表明,随着模拟投针次数的增大,所计算的的近似值越来越接近于其
真值,而要进行这样的数值模拟,就需要很大的计算量,只有利用计算机才能实现。
- 4 -
剩余63页未读,继续阅读
qq_43413427
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- RTL8188FU-Linux-v5.7.4.2-36687.20200602.tar(20765).gz
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论1