一维弹塑性本构编程入门

umat

本构方程

需积分: 36 53 浏览量更新于2023-05-22 3 收藏 250KB PDF 举报

一维弹塑性本构程序入门，包括公式推导，和伪代码给出，涉及到牛顿拉弗逊迭代，几种硬化模型，我觉得对写uamt来说帮助非常大，虽然说这个不是umat教程，但是绝对值得一看，非常棒的入门手册，新手入门很容易，

Nonlinear Static - 1D Plasticity - Various Forms of Isotropic Hardening

by Louie L. Yaw

Walla Walla University

Draft Date January 25, 2012

key words: plasticity, algorithms, nonlinear analysis, isotropic hardening, algorithmic tan-

gent modulus, elasto-plastic tangent modulus, Kuhn-Tucker conditions, consistency param-

eter, internal hardening variable, equivalent plastic strain, ﬂow rule, consistency condition,

yield condition

1 Introduction

Metals loaded beyond the elastic limit deform plastically. It is often the goal in structural

mechanics to model plastic deformations of such metals in a computational setting. Creating

algorithms to model the combined eﬀect of elastic and plastic deformations is not trivial.

However, plasticity for the one dimensional case is a good introduction to the concepts

necessary to construct such algorithms. Hence, this article presents plasticity from a one

dimensional point of view and derives algorithms for a variety of diﬀerent ha r d en i n g models.

It is the g oal of this article to introduce students to algorithmic plasticity (nonlinear material)

models and also pave the way for future learning in the area of three dimensional plasticity.

One dimensional plasticity is hel p fu l as an introduction and as an intermediate step to-

ward more diﬃcult topics, but it is also practical for bar elem ents often modeled in structural

analysis software. It is therefore worth noting that the information learn ed herein i s useful

for the implementation of plasticity by modifying a standar d linear truss analysis program.

Only small strains are considered.

2 Elastic and plastic behavior

Material testing is often accomplished by tensile tests. Plots of stress versus strain are often

created from tension tests. For many materials the plot of stress versus strain is linear for

stresses below a certain threshold called the yield stress. If the material is loaded beyond this

point the material yields and begins to deform plastically. How the material deforms after

passing t h e yield point varies from material to material. For instance many materials exhibit

hardening after reaching the yield limit. This hardening is exhibited by increasing resistance

to load after yielding, but th i s increase in resistance is much less than the resistance provided

by the material before yi el d i n g .

If hardening is present the post yield behavior exhibits both increasing elastic strain and

increasing plastic strain. A variety of models are availab l e to try and s imulate how the

plastic strain increases with increasing stress. The post yield behavior is often modeled

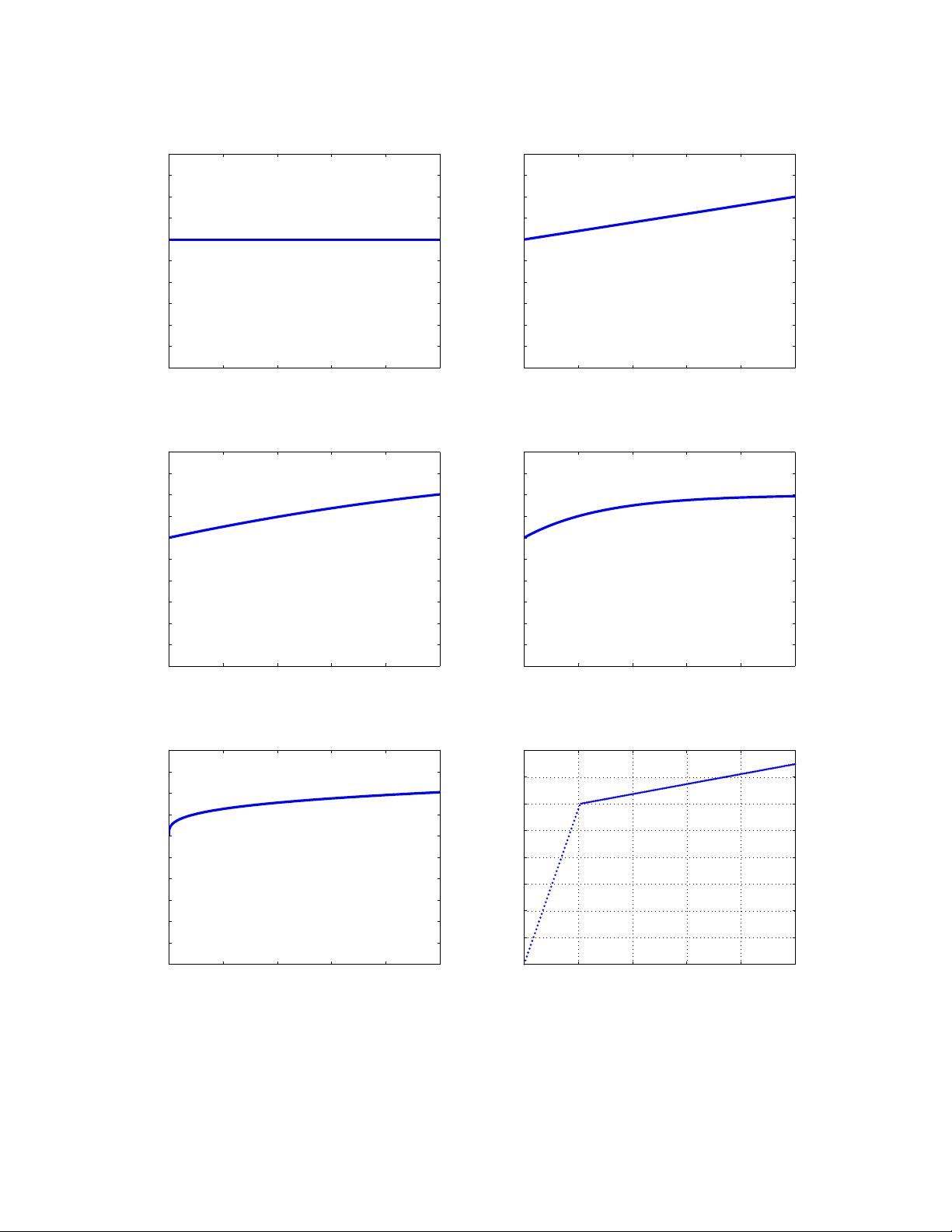
by specifying how the yield stress evolves with increasing plastic strain. A variety of such

models are shown in Figure 1. In the plots the yield point is shown, σ

= 30 ksi, a n d the

hardening behavior is plotted based on the formulas sh own. It is important to note that the

plots are of stress versus plastic strain. When plots of stress versus total strain a re created

based on these models, the post yi el d behavior will look si m i la r but will be diﬀerent since

the post yield behavior also accounts for increasing elastic strains. Hence, for example, in

the case of Figure 1(b) the post yield slope is called the plastic modulus. Wher eas a plot of

stress versus total strain using linear hardening, Figure 1(f), has a post yield slope that is

called the elasto-pl as ti c modulus and it is not the same as the plastic modulus. Because of

hardening the yield p oi nt has increased and as a result more elastic strain exi st s due to the

higher yi eld point. Hence, for hardening materials, in cr eas e in pl as ti c strain is accompanied

with increase in elastic strain. In later sections the derivat i on of the elasto-plastic modulus

is illustrated for the models given.

3 Deﬁnitions

Basic termino lo gy helpful for understanding the concepts involved in modeling plasticity is

presented in this section. The deﬁnitions given are not exhau st i ve, but provide at least the

basic ideas. S o m e of the terms are easy to deﬁn e clearly. Other terms can be deﬁned but are

better understood after working with the material in following secti on s . The notation used

closely follows that given by Simo and Hughes [6].

Brief deﬁnitions of the m ost important terminolo gy are as follows. Elastic strain, ε

, is

any strain that takes place before exceeding the yield stress. However, it is important t o

note that, for harden i ng materials, elastic strain is increasing during post yield also. Hence,

strain that is rem oved during unloading is a better deﬁnition of elastic strain. Plasti c strain,

, is permanent strain that remains after unloading. Total strain is the sum of elastic strain

and plastic strain, ε = ε

+ ε

. Any time plastic strains are taking place it follows that

plastic ﬂow is taking place. When hardening occurs the value of the yield stress changes.

For this reason, plasticity models u se internal h ar dening variables as a means for keeping

track of accumulated hardening. For isotropic har dening, hardening accumulates if p l as ti c

strain is p osi t i ve or negative, hence the internal hardening variable keeps track of the total

change in plastic strain. Therefore, the isotropic internal hardening variable α is called the

equivalent plastic strain. A yield cond i t io n (a funct i on ) is used to mathemat i cal l y id entify

when yielding happens. Often in the literature the yield condi t i on i s denoted by f. It

typically includes the current level of stress minus the init i al yield stress added to a function

of α which describes the typ e of hardening. Examples of yield conditions are p r ovided later

in this paper. As plastic st ra i n takes place, α is updated and changes, the yield condition f

is calculated and is either a negative value or a positive value. If it is negative the current

level of stress is below y ie ld and only elastic strains are increasing. If it is positive th e

current level of stress is a bove the yield stress and (with the presence of hardening) elastic

and plastic strains are increasing. However, in a ct u al i ty f > 0 is not allowed and requires

calculation o f the amount of plastic ﬂow and how the hardening level evolves such that f = 0

is achieved. This is accomplished by solving for a consistency parameter γ, which allows a

means for determining the level of plastic ﬂow and hardening such that t h e condition f = 0

is satisﬁed. The variable γ is called th e consistency parameter because it is deteremined so

that all relevant variables are consistent with the requirement that f = 0 when plastic ﬂow is

taking place. This is a rather involved process and is diﬃcult to describe in words. The whole

process of elastic loading and unloading or elasto-plastic loading and unloading requires a

careful mathematical description. This has led researchers to u se Kuhn - Tucker cond i t i on s.

The Kuhn- Tucker conditions are γ ≥ 0, f(σ) ≤ 0, and γf(σ) = 0. These conditions or rules

are used to construct the mathematical algor i thms which model the process of plastic ﬂow

(for a more in depth discussion th e reader i s referred to Simo and Hughes [6]). A consi st ency

condition is also used and is written as γ

f = 0, if f = 0. The sign function i s often used in

the mathematics of plasticity algorith m s . The function takes any var ia b l e and returns − 1 if

the variable is negative and +1 if the variab l e is positive. Plasticity algorithms are often used

in ﬁnite element analysis programs to model nonli n ear material behavior. In such cases the

ﬁnite element analysis program is incremental in nature. Each new load increment increases

stress levels, strain levels and displacements. Hence, d u r i n g each of these increments the

plasticity algori t h m is used at the elem ent l evel in the analysis program. At the beginning of

each increment (or load step) it is not known wh et h er the new level of stress cau se s yielding

(in a pa r ti cular element) or not. For this reason it is initially assume d that the incremental

stress is elastic. In the plasticity algorithms, the resulting new stress level is termed a trial

stress. This trial stress is plugged into the yield condition f and the rules of th e algorithm

are followed as necessary. In the course of the algorithm the correct new str ess level is

determined (ie, the trial stress is corrected if the stress incr em ent was not entirely elastic).

In some derivations given in this paper derivatives with respect to time such as

dα

= ˙α are

used. However, the type of m at er i al models described in this paper are rate independent,

so it may seem odd to take derivatives with r espect to time. Hence, in this setting the

interpretation of derivatives with respect to time really mean changes with respect to a load

step or load increment in a ﬁnite el em ent analysis program. For example, if the current value

of the internal var i able α is α

then during the load in cr e m ent the variable may increase by an

amount ∆α such that the new va lue of α is α

n+1

= α

+∆α. In this example ∆α is analogous

to ˙α. Ano t h er way to look at this is to say that (in a rate independent material model) a load

increment is like a time increm e nt. This is the reason derivatives with respect to time are used

in the literature even in rate independent material models. In some theoretical derivations

γ i s us ed to den ot e the consi st en cy p ar am et er . However, in the plasticity model algorithms

∆γ is used to denote the consistency paramenter. Otherwise, there is no diﬀerence between

γ and ∆γ used in th i s paper. For t he 1D plasticity case th e algorithmic tangent m odulus

is equivalent to the elasto-plastic modulus. In higher dimensions this is not true. For some

plasticity models the yield function is complicated enough that algebr ai cal l y solving for the

consistency par am et er is not possible and hence it must be solved for using Newton-Raphson

iterations. In this process, in order to preserve the second order rate of convergence of the

Newton-Raphson method (which is likely also taking place at the global level of the nonlinear

ﬁnite element program) it is necessary to have a consistent variation (or d er i vative) of stress

with respect to the total s t ra i n . To get such a consistent variation it is necessary to t a ke the

derivative of th e algorithmic stress wit h respect to the total strain varia b l e. The al gor i t h m i c

tangent modulus is speciﬁcally derived by taki n g the derivative

∂σ

(k)

n+1

∂ε

(k)

n+1

= C

(k)

n+1

. This is a

derivative of the algorithmic stress and hence results in th e a l gor i t h m i c tangent modulus,

(k)

n+1

. How plastic strain evolves in pl as t ici ty algorithms is called a ﬂow rule. In this paper

the ﬂow r u l e takes the form ˙ε

= γ

dσ

= γsign(σ). The isotropic hardening law takes the

form ˙α = ∆α = γ.

剩余24页未读，继续阅读

qq_15272621

粉丝: 4

一维弹塑性本构编程入门

最新资源