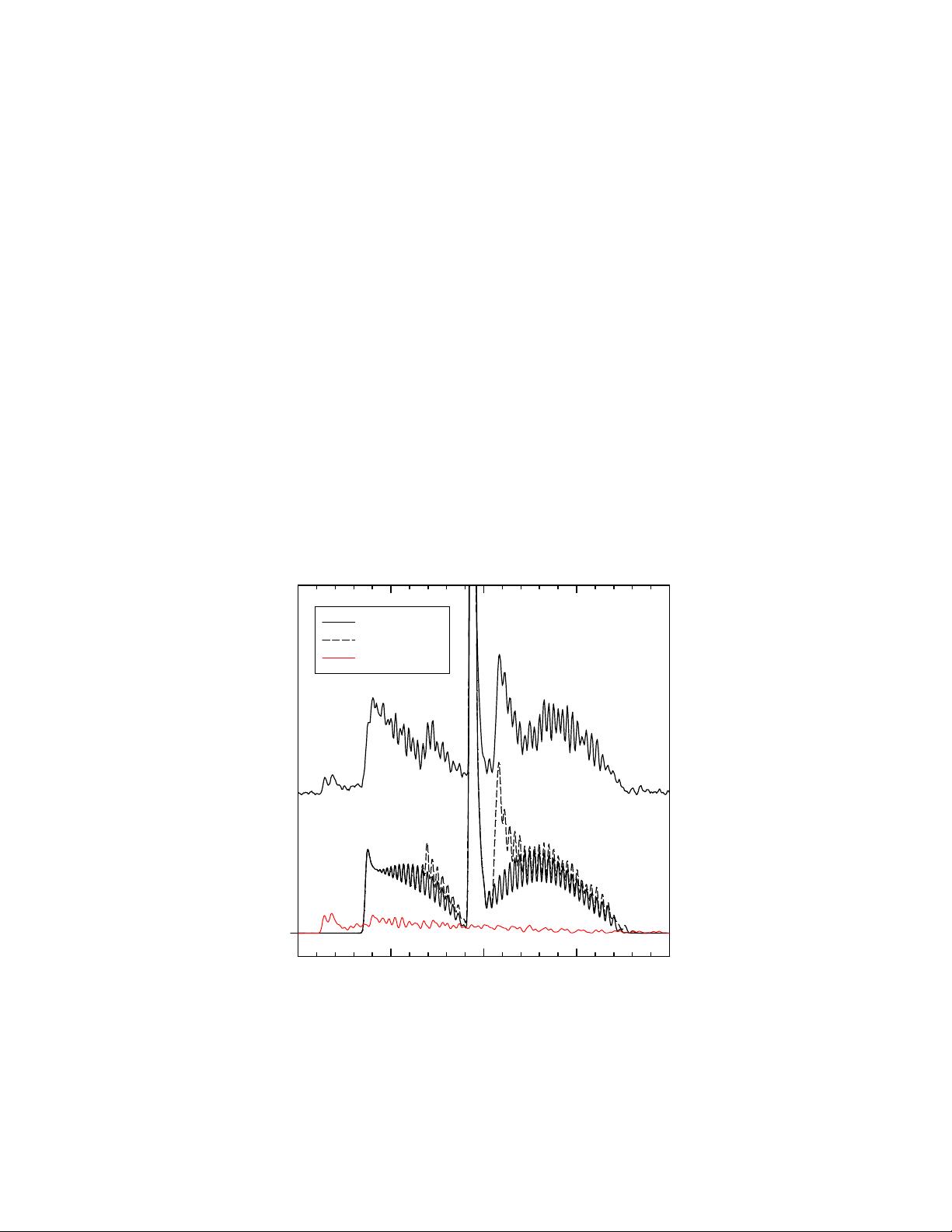
4
d)
Frequencies
: These are calculated from expressions derived from the
corresponding Hamiltonians (most cases this is the N-formalism, known as Brown’s
Hamiltonian
6
), so the accuracy of line-positions may be limited in some cases. The units
are cm
-1
, Å (vacuum) or Å (air).
The nomenclature of the branches is either Hund’s case
a
or
b
. The program
supports both cases switching with the “J” and “N” keys. In Hund’s case
b
the name of
the rotational branches is given by
∆
N =N’-N” rather than
∆
J (N’, excited state; N”,
ground state):
Case a:
∆
N
∆
J
F’F”
(J”) Case b:
∆
J
∆
N
F’F”
(N”)
and
∆
N or
∆
J =-2,-1,0,1,2
!
O,P,Q,R,S
The rotational lines are assigned by N quantum numbers in Hund’s case
b
, this
notation can be changed to J numbers, Hund’s case
a
. The lines with ground state
terms from the spin-orbit F
1
: J=N+1/2 and from F
2
: J=N-1/2. For example:
NO A-X
R
R
11
(N”=1) [case b] ->
R
R
11
(J”=1.5) = R
1
(1.5) [case a]
e) Line-strengths or
Hönl-London factors
: Following the analytical expressions
by Kovacs
7
and Earls
8
. The normalization is as suggested by Whiting
9
:
SSJ
J
J
J
"
'
"
,' "
()(')(')
∑
=− + +
+
22121
0
δ
ΛΛ
f)
Lifetimes
are calculated by:
τ
vJ
e
vJ
vJ
vJ
g
A
''
'
""
''
""
=
∑
and normalized to the chosen experimental
τ
v’=0
(in ns).
g)
Predissociation
rates (Kp
v’J’
) and
quenching
(Kq
v’J’
) rate coefficients can be
included in the calculation of fluorescence quantum yields through user provided files.
The program comes with the most accurate predissociation rates known, and the
quenching set to zero. The column title to identify radiative lifetime is
t
r
collision free
lifetime is
t
p
, and the fluorescence quantum yield including quenching is
Y
f
.
Also, one can choose to study a particular vibrational band and obtain a
complete table with the main and the satellite branches. Finally, the program is able to
print or create a file with the selections made.