Memristor-The Missing Circuit Element

需积分: 10 105 浏览量更新于2023-06-22 收藏 995KB PDF 举报

\Memristor-The Missing Circuit Element原始版

,EEE TRANSACTIONS ON CIRCUIT THEORY, VOL. CT-18, NO.

SEPTEMBER

1971

507

Memristor-The Missing Circuit Element

LEON 0. CHUA,

SENIOR MEMBER, IEEE

Abstract-A new two-terminal circuit element-called the memrirtor-

characterized by a relationship between the charge q(t) s St% i(7J

and the

flux-linkage (p(t) = J-‘-m vfrj

T is introduced os the fourth boric

circuit element. An electromagnetic field interpretation of this relationship

in terms of a quasi-static expansion of Maxwell’s equations is presented.

Many circuit~theoretic properties of memdstorr are derived. It is shown

that this element exhibiis some peculiar behavior different from that

exhibited by resistors, inductors, or capacitors. These properties lead to a

number of unique applications which cannot be realized with

RLC

net-

works alone.

”

-3

Although a physical memristor device without internal power supply

has not yet been discovered, operational laboratory models have been

built with the help of active circuits. Experimental results ore presented to

demonstrate the properties and potential applications of memristors.

(a)

1NTR00~cnoN

-3

HIS PAPER presents the logical and scientific basis

for the existence of a new two-terminal circuit element

called the memristor (a contraction for memory

(b)

resistor) which has every right to be as basic as the three

classical circuit elements already in existence, namely, the

resistor, inductor, and capacitor. Although the existence

of a memristor in the form of a physical device without

internal power supply has not yet been discovered, its

laboratory realization in the form of active circuits will be

presented in Section II.’ Many interesting circuit-theoretic

properties possessed by the memristor, the most important

of which is perhaps the passivity property which provides

the circuit-theoretic basis for its physical realizability, will

be derived in Section III. An electromagnetic field in-

terpretation of the memristor characterization will be pre-

sented in Section IV with the help of a quasi-static expansion

of Maxwell’s equations. Finally, some novel applications

of memristors will be presented in Section V.

”

-3

”

(cl

Cd)

II.

MEMRISTOR-THE FOURTH BASIC

CIRCUIT ELEMENT

From the circuit-theoretic point of view, the three basic

two-terminal circuit elements are defined in terms of a

relationship between two of the four fundamental circuit

variables, namely;the current i, the voltage v, the charge q,

Fig. 1. Proposed symbol for memristor and its three basic realizations.

(a) Memristor and its q-q curve. (b) Memristor basic realization 1:

M-R

mutator terminated by nonlinear resistor &t. (c) Memristor

basic realization 2:

M-L

mutator terminated by nonlinear inductor

C. (d) Memristor basic realization 3:

M-C

mutator terminated by

nonlinear capacitor e.

Manuscript

received November 25, 1970; revised February 12,197l.

This research was supported in part by the National Science Foundation

under Grant GK 2988.

The author was with the School of Electrical Engineering, Purdue

University, Lafayette, Ind. He is now with the Department of Electrical

Engineering and Computer Sciences, University of California, Berke-

ley, Calif. 94720.

r In a private communication shortly before this paper went into

press, the author learned from Professor P. Penfield, Jr., that he and

his colleagues at M.I.T. have also been using the memristor for model-

ing certain characteristics of the varactor diode and the partial super-

conductor. However, a physical device which corresponds exactly to a

memristor has yet to be discovered.

and theflux-linkage cp. Out of the six possible combinations

of these four variables, five have led to well-known rela-

tionships [l]. Two of these relationships are already given

by q(t)=JL w i(T) d

7 and cp(t)=sf. m D(T) d7. Three other rela-

tionships are given, respectively,. by the axiomatic definition

of the three classical circuit elements, namely, the resistor

(defined by a relationship between v and i), the inductor

(defined by a relationship between cp and i), and the capacitor

(defined by a relationship between q and v). Only one rela-

tionship remains undefined, the relationship between 9

and q. From the logical as well as axiomatic points of view,

it is necessary for the sake of completeness to postulate the

existence of a fourth basic two-terminal circuit element which

Authorized licensed use limited to: IEEE Publications Staff. Downloaded on December 4, 2008 at 14:12 from IEEE Xplore. Restrictions apply.

IEEE

TRANSAcrlONS

CIRCUIT

THEORY,

VOL.

cr-18,

No.5,

SEPTEMBER

1971

507

Memristor-The Missing Circuit Element

LEON

CHUA,

SENIOR MEMBER,

IEEE

(

;.*

y.*

-----:>I~------:"

;=)m

(a)

;=)

(b)

(c)

(d)

Fig.

Proposed symbol for memristor and its three basic realizations.

(a) Memristor and its

qrq

curve. (b) Memristor basic realization

M-R

mutator terminated by nonlinear resistor

CR.

basic realization 2:

M-L

mutator terminated by nonlinear inductor

.c.

(d) Memristor basic realization 3:

M-C

mutator terminated by

nonlinear capacitor

and theflux-linkage

'P.

Out

the

six

possible combinations

these four variables,

five

have led

well-known rela-

tionships [I]. Two

these relationships are already given

q(t)=

i(T)

and «J(t)=

v(T)

dT.

Three other rela-

tionships are given, respectively,. by the

axiomatic definition

the three classical circuit elements, namely, the resistor

(defined by a relationship between v and i), the inductor

(defined by a relationship between

and i), and the capacitor

(defined by a relationship between q and

v).

Only one rela-

tionship remains undefined, the relationship between

and

From

the logical as well as axiomatic points

view,

necessary for the sake

completeness to postulate the

existence

a fourth basic two-terminal circuit element which

II.

MEMRISTOR-

THE

FOURTH

BASIC

CIRCUIT

ELEMENT

From

the circuit-theoretic point of

view,

the three basic

two-terminal circuit elements are defined in terms

relationship between two

the four fundamental circuit

variables, namely,.the

current

the voltage

the charge q,

Manuscript received November

25,

1970; revised February

12,

1971.

This research was supported in part by the National Science Foundation

under Grant

GK.

2988.

The author was with the School

Electrical Engineering, Purdue

University, Lafayette, Ind. He

now with the Department

Electrical

Engineering and Computer Sciences, University

California, Berke-

ley, Calif.

94720.

1 In a private communication shortly before this paper went into

press, the author learned from Professor P. Penfield,

Jr., that he and

his colleagues

M.I.T. have also been using the memristor for model-

ing certain characteristics

the varactor diode and the partial super-

conductor. However, a physical device which corresp0nds exactly to a

memristor has yet to be discovered.

I. INTRODUCTION

HIS PAPER presents the logical and scientific basis

for

the

existence

a new two-terminal circuit element

. called the

memristor (a contraction for

memory

resistor) which has every right to be as basic as the three

classical circuit elements already in existence, namely, the

resistor, inductor, and capacitor. Although the existence

a memristor in the form

a physical device without

internal power supply has not yet been discovered, its

laboratory realization in the form

active circuits will be

presented in Section

11.

Many interesting circuit-theoretic

properties possessed by the memristor, the most important

which is perhaps the passivity property which provides

the circuit-theoretic basis for its physical realizability, will

be derived in Section III. An electromagnetic field in-

terpretation

the memristor characterization will be pre-

sented in Section IV with the help

a quasi-static expansion

Maxwell's equations. Finally, some novel applications

memristors will be presented in Section

Abstract-A

new

two-terminal

circuit

element-called

the

memrislor-

characterized

relationship

between

the

charge

q(I}

-'"

i(r}

and

the

flux-linkage

<p(I}

f'-", vir}

introduced

the

fourth

basic

circuit

element.

electromagnetic

field

interpr'!tation

this

relationship

terms

quasi-static

expansion

Maxwell's

equations

presented.

Many

circuit· theoretic

properties

memristors

are

derived.

It is

shown

that

this

element

exhibiis

some

peculiar

behavior

different

from

that

exhibited

resistors, inductors,

capacitors.

These

properties

lead

to a

number

unique

applications

which

cannot

realized

with

RLC

net-

works

alone.

Although

physical

memristor

device

without

internal

power

supply

has

not

yet

been

discovered,

operational

laboratory

models

have

been

built

with

the

help

active

circuits.

Experimental

results

are

presented

demonstrate

the

properties

and

potential

applications

memristors.

508

IEEE TRANSACTIONS ON CIRCUIT THEORY, SEPTEMBER 1971

TABLE I

CHARACTERIZATION AND REALIZATION OF

M-R, M-L,

AND

M-C

MUTATORS

‘PE

RANSMISSION MATRIX

::I = [T(P’][J

BASH: REALIZATIONS

USING CONTROLLED SOURCES

SYMBOL

AND

CHARACTERIZATION

’ :

REALIZATION 2

REALIZATION I

‘2

w+gf

“2

D---a

I c

(2) + i2+

“2

(li,dt)

F--a-

+(!%) -i2+

“2

Uqdt) -

P 0

~R,b) =

[ 1

0 P

dVp

“I= dt

dip

iI = -7

(q.Vl -RvR,iR)

Y-R

MUTATOR REALIZATION I

REALIZATION 2

di2

VI’ -7

REALIZATION 2

REALIZATION I

gq-:

Identical to TcR,(p)

f c Type I C-R MUTATOR 1

REALIZATtON 4

REALIZATION 3

REALIZATION I

“I = “2

di2

iI=-

!TDq-y

I +(!!k)

i2+

(VI)- “!

M-L

MUTATOR

REALIZATION 2

(q,# -WL, iL)

di,

v, = - dt

i, =v2

0 P

TML2fP” ) o

[ 1

(Identical to TLR2(p)

mf c Type 2 L-R MUTATOA

REALIZATION 2

:f-pq*

REALIZATlON I

i, = - i2

P 0

k,(P) o (

[ 1

(I&tical 10 TLRltp)

d a Type I L-R MUTATOR

I ;

REALlZATlON 3

REALIZATlON 4

M-C

MUTATOR

REALIZATION I

v, =-i

d”2

il =r(t

REALIZATION 2

r. ,-

(ipI

-D---a

“I

;

t/ildt)- I

3pq

“2

blcp=

p o

(Idtmticdl

t0 TCR2 ( p)

,f a Type 2 C-R WTATOF

Authorized licensed use limited to: IEEE Publications Staff. Downloaded on December 4, 2008 at 14:12 from IEEE Xplore. Restrictions apply.

508

IEEE

TRANSACTIONS

CIRCUIT

THEORY, SEPTEMBER

1971

TABLE I

CHARACTERIZATION

AND

REALIZATION

M-R,

M-L,

AND

M-C

MUTATORS

TRANSMISSION

MATRIX

SYMBOL

[~:

]

[

T(P)]

~::]

BASIC

REALIZATIONS

TYPE

AND

CHARACTERIZATION

USING

CONTROLLED

SOURCES

d£te

REALIZATION

",{

;i-[J'~')

,f~

;i-@,:,')

.f~

t !

: t v

1·-

dV2

I 0

(/vldt)

(/ildtl

1----4

VI'

M·R

-dT

MUTATOR

REALIZATION I REALIZATION

l;i-~~).t

;i-[J~~;)

",{

:;:

! v

t v

- 2 -

di2

2 P

1';.-

(/ildtl

(/vldt)

f.--4

=--

i I •

REALIZATION I REALIZATION

+ +

~1'/lldt)

(q,9?)"""'"

(IL,cPLl

)

'.C

",{

-"'jjf

- -

I 0

- I -

REALIZATION 3 REALIZATION 4

VI"

(Identical

TCR,(

;i-@*),,~

Type

CoR

MUTATOR)

~[l',{~

M-L

II'-dl

: t v2

t :

MUTATOR

"--

(/lldtl

.0--

(vI)

(q,~)-(jPL.iL)

REALIZATION I

REALIZATION 2

'~R>'

'.C

",{

(v2'

~~~)

§""

2 I

+ !

- 2 -

(Identical

TLR2

(p)

)

(il)_

VI'

• v2

of a

Type

L-R

MUTATOR)

REALIZATION

I REALIZATION 2

+ + +

(q,tp) -

(qc'v

)

(~-

)

lIvldt-v,

)

'Me

",{

- - -

I 0

- I -

REALIZATION 3

REALIZATION

•

dV2

(Identical

TLR

( p)

~@~).,lE

~@",

..f

Type

L-R

MUTATOR)

M-C

i,"

- 1

v, :

t +

MUTATOR

(i,)

(/Vldt)-

.'!')

-(vc,qc)

REALIZATION I

REALIZATION 2

'.c,"'{

]

[Jr.)

r+-

,,;t

r-"+

- 2 -

(/ll

• - i

(Identical

TCR2

(p)

r---4

(VI)

I----i

. dV2

Type

CoR

MUTATOR)

II :

Cit

CHUA: MEMRISTOR-MISSING CIRCUIT ELEMENT

509

+Ecc

014

l?&l50)

R4( IOOK)

RJ9lO)

(2~4236)

I f I 1 1 h-b--&

1 AR, 1 SO-IOA JRLq-

I I

’ *-kc

- +

“2

- -

Port 2

Fig. 2. Practical active circuit realization of type-l

M-R

mutator based on realization 1 of Table I.

is characterized by a cp-q curve.2 This element will hence-

forth be called the memristor because, as will be shown later,

it behaves somewhat like a nonlinear resistor with memory.

The proposed symbol of a memristor and a hypothetical

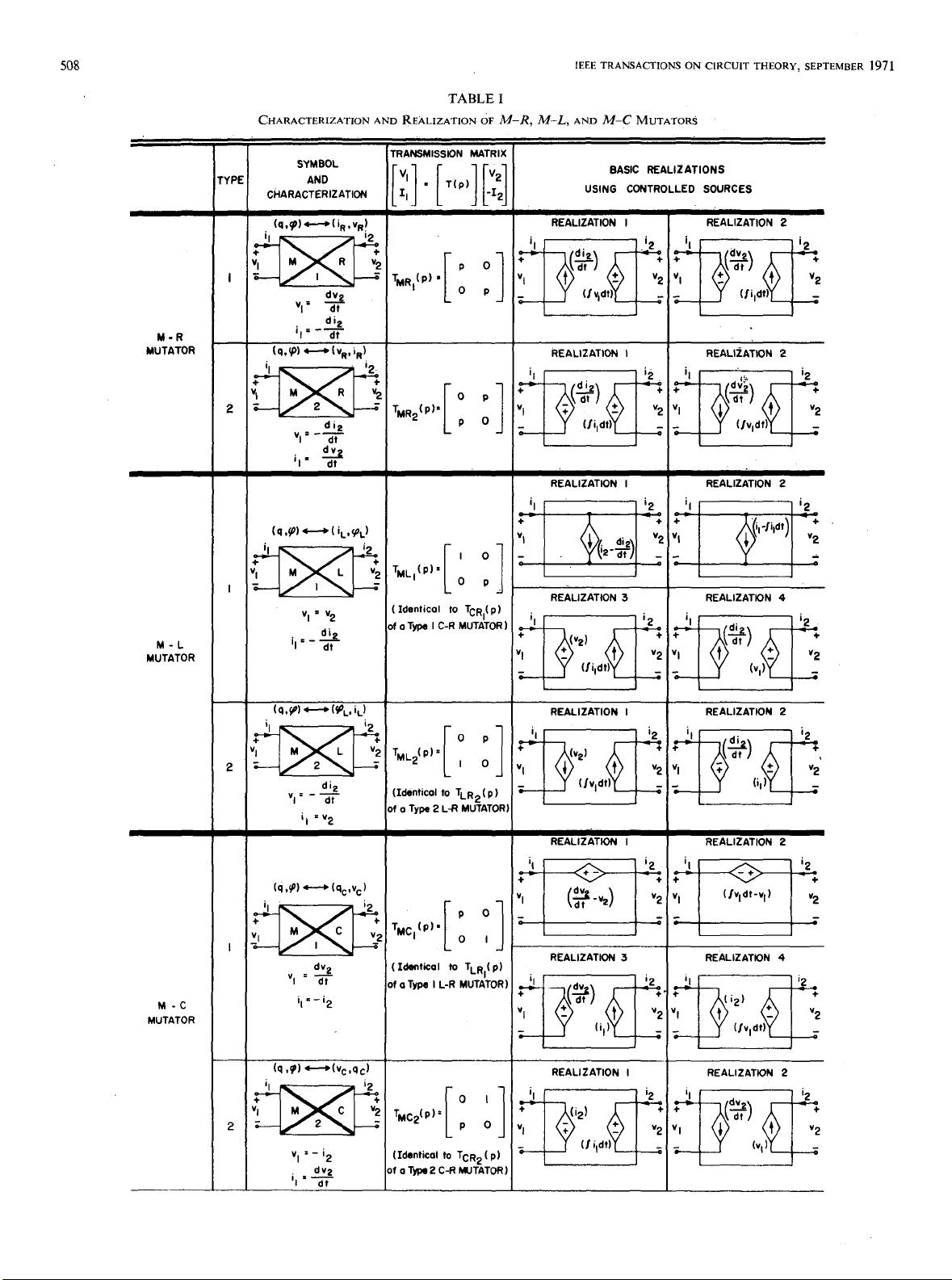
cp-q curve are shown in Fig. l(a). Using a ,mutator [3], a

memristor with any prescribed p-q curve can be realized

by connecting an appropriate nonlinear resistor, inductor, or

capacitor across port 2 of an M-R mutator, an M-L

mutator, and an M-C mutator, as shown in Fig. l(b), (c),

and (d), respectively. These mutators, of which there are

two types of each, are defined and characterized in Table I.3

Hence, a type-l M-R mutator would transform the uR-if<

curve of the nonlinear resistor f(u,+ iR)=O into the corre-

sponding p-q curvef(cp, q)=O of a memristor. In contrast

to this, a type-2 M-R mutator would transform the iR-vR

curve of the nonlinear resistor f(iR, uR)=O into the corre-

sponding p-q curvef(9, q) = 0 of a memristor. An analogous

transformation is realized with an M-L mutator (M-C

mutator) with respect to the ((PL, iL) or (iL, cp~) [(UC, qc) or

(qc, UC)] curve of a nonlinear inductor (capacitor).

Each of the mutators shown in Table I can be realized

by a two-port active network containing either one or two

controlled sources, as shown by the various realizations in

Table 1. Since it is easier to synthesize a nonlinear resistor

with a prescribed u-i curve [l], only operational models of

k-R mutators have been built. A typical active circuit

realizatian based on realization 1 (Table I) of a type-l

M-R mutator is given in Fig. 2. In order to verify that a

memristor is indeed realized across port 1 of an M-R muta-

tor when a nonlinear resistor is connected across port 2, it

2 The postulation of new elements for the purpose of completeness

of a physical system is not without scientific precedent. Indeed, the

celebrated discovery of the periodic table for chemical elements by

Mendeleeff in 1869 is a case in point [2].

3 Observe that a type-l (type-2)‘M-L mutator is identical to a type-l

(type-2)

C-R

mutator (L- R’mutator). Similarly, a type-l (type-2)

M-C

mutaror is identical to a type-l (type-2)

L-R

mutator

(C-R

mutator).

would be necessary to design a p-q curL;e tracer. The com-

plete schematic diagram of a practical p-q curve tracer is

shown in Fig. 3.4 Using this tracer, the p-q curves of three

memristors realized by the type-l M-R mutator circuit of

Fig. 2 are shown in Fig. 4(b), (d), and (f) corresponding to

the nonlinear resistor V-Z curve shown in Fig. 4(c), (e), and

(g), respectively. To demonstrate the rather “peculiar”

voltage and current waveforms generated by the simple

memristor circuit shown in

Fig.

5(a), three representative

memristors were synthesized with q--q curves as shown in Fig.

5(b), (d), and (f), respectively. The oscilloscope tracings of

the voltage u(t) and current i(t) of each memristor are shown

in Fig. 5(c), (e), and (g), respectively. The waveforms in

Fig. 5(c) and (e) are measured with a 63-Hz sinusoidal input

signal, while the waveforms shown in Fig. 5(g) are measured

with a 63-Hz triangular input signal. It is interesting to ob-

serve that these waveforms are rather peculiar in spite of the

fact that the cp-q curve of the three memristors are relatively

smooth. It should not be surprising, therefore, for us to

find that the memristor possesses certain unique signal-

processing properties not shared by any of the three existing

classical elements. In fact, it is precisely these properties that

have led us to believe that memristors will play an important

role in circuit theory, especially in the area of device model-

ing and unconventional signal-processing applications. Some

of these applications will be presented in Section V.

III. CIRCUIT-THEORETIC PROPERTIES OF MEMRISTORS

By definition a memristor is characterized by a relufiorz

of the type g(;p, q)=O. It is said to be charge-controlled

(flux-controlled) if this relation can be expressed as a single-

valued function of the charge rZ (flux-linkage a). The voltage

4 For additional details concerning the design and operational char-

acteristics of the circuits shown in Figs. 2 and 3, as well as that for a

type-2

M-R

mutator, see [4].

Authorized licensed use limited to: IEEE Publications Staff. Downloaded on December 4, 2008 at 14:12 from IEEE Xplore. Restrictions apply.

CHUA:

MEMRISTOR-MISSING

CIRCUIT ELEMENT

509

r-------------,....----~--~---o+Ecc

'------------------

........

---.4---E

(2N4236)

~j=

l~Z

Port I

Port

Fig.

Practical active circuit realization

type-!

M-R

mutator

based

realization!

Table I.

characterized by a

<P-q

curve.

This element will hence-

forth be called the

mernristor because, as will be shown later,

it behaves somewhat like a nonlinear resistor with memory.

The proposed symbol

a memristor

and

a hypothetical

<P-q

curve are shown in Fig. lea). Using a

mutator

[3], a

memristor with any prescribed

<P-q

curve can be realized

by connecting an appropriate nonlinear resistor, inductor,

capacitor across

port

M-R

mutator,

anM-L

mutator, and an

M-C

mutator, as shown in Fig.

l(b),

(c),

and (d), respectively. These mutators,

which there are

two types

each, are defined

and

characterized in Table

J.3

Hence, a type-l

M-R

mutator

would transform the vR-i

curve

the nonlinear resistor

Ii,

iii) = 0 into the corre-

sponding

<p-q

curvef(<p,

q)=O

a memristor. In contrast

to this, a type-2

M-R

mutator

would transform the

ili-VR

curve

the nonlinear resistor

fUIi,

VIi)=O into

the

corre-

sponding

<P-q

curvef(<p, q) = 0

a memristor. An analogous

transformation

realized with an

M-L

mutator

(M-C

mutator) with respect

the

(<PL'

iL)

(iL,

<pd

[(vc,

qc)

(qc, vc)] curve

a nonlinear inductor (capacitor).

Each

the mutators shown in Table I can be realized

by a two-port qctive network containing either one or two

controlled

sour~es,

as shown by the various realizations in

Table

Since it

easier to synthesize a nonlinear resistor

with a prescribed

v-i

curve [I], only

op~rational

models

M-R

mutators have been built. A typical active circuit

realization

based on realization I (Table I)

a type-l

M-R

mutator

given

Fig.

In order

verify

that

memristor

indeed realized across

port

M-R

muta-

tor

when q nonline'ar resistor

connected across

port

2 The postulation

new elements for the purpose

completeness

a physical system

not without scientific precedent. Indeed, the

celebrated discovery

the periodic table for chemical elements by

Mendeleeff

1869

ca'se.

point [2].

S Observe that a type-I (type-2)

M-L

mutator

identical to a type-!

(type-2)

C-R

mutator

(L-Rmutator).

Similarly, a type-! (type-2)

M-C

mutator

identical

a type-! (type-2)

L-R

mutator

(C-R

mutator).

would be necessary

design a

<P-q

curve tracer. The com-

plete schematic diagram

a practical

<p-q

curve tracer

shown in Fig.

Using this tracer,

the

<p-q

curves

three

memristors realized by

the

type-l

M-R

mutator

circuit

Fig. 2 are shown in Fig. 4(b), (d),

and

(f)

corresponding

the

nonlinear resistor

V-I

curve shown in Fig. 4(c), (e),

and

(g), respectively.

demonstrate the rather "peculiar"

voltage

and

current waveforms generated by the simple

memristor circuit shown in Fig. 5(a), three representative

memristors were synthesized with

<p'-q

curves as shown in Fig.

S(b), (d),

and

(0, respectively. The oscilloscope tracings

the voltage v(t) and current i(t)

each memristor are shown

in Fig. S(c), (e), and (g), respectively.

The

waveforms in

Fig.

S(c)

and (e) are measured with a 63-Hz sinusoidal input

signal, while

the

waveforms shown in Fig.

S(g)

are measured

with a 63-Hz triangular

input

signal.

interesting

ob-

serve

that

these waveforms are rather peculiar in spite

the

fact

that

the

<P-q

curve

the three memristors are relatively

smooth.

should

not

be surprising, therefore, for us

find

that

the memristor possesses certain unique signal-

processing properties

not

shared by any of the three existing

classical elements.

fact, it

precisely these properties

that

have led us

believe

that

memristors will play an

important

role in circuit theory, especially in the area

device model-

ing

and

unconventional signal-processing applications. Some

these applications will

presented in Section

Ql.

CIRCUIT-THEORETIC

PROPERTIES OF

MEMRISTORS

definition a memristor

characterized by a relation

the type

g(<p,

q)=O.

said

be charge-controlled

(flux-controlled) if this relation can be expressed as a single-

valued function

the charge q (flux-linkage

<p).

The

voltage

4 For additional details concerning the design

and

operational char-

acteristics

the circuits shown in Figs. 2

and

as well as that for a

type-2

M-R

mutator, see

[41.

剩余12页未读，继续阅读

why0521

粉丝: 0
资源: 2

Memristor-The Missing Circuit Element

最新资源