Matlab计算重积分指南

"该资源是Matlab实验教程，专注于重积分的计算和应用，适合初学者。通过实验，学习者可以掌握如何使用Matlab进行二重积分和三重积分的计算，并解决相关应用问题。实验内容包括在直角坐标和极坐标系下进行二次积分的转化，以及使用Matlab的相关命令进行积分操作。" 在Matlab中计算重积分是一项重要的技能，特别是在解决数学问题和工程应用中。实验9《重积分》主要关注的是如何利用Matlab这个强大的数学工具来处理复杂数学计算，特别是二重积分和三重积分。 首先，二重积分是在二维平面上计算面积的一种方式，它通常用于求解曲面下的面积、物理问题中的体积和质量等问题。在直角坐标系下，二重积分可以通过将积分区域划分为多个小矩形，然后累加每个矩形的面积来近似。而在极坐标下，二重积分则转换为对角度和半径的积分，这在处理圆形或对称性较强的区域时更为便捷。在Matlab中，可以使用`int`函数进行二重积分的计算，例如例1所示，计算积分`∫∫(x^2+y^2)dxdy`，在-1到1的区间内，结果为`8/3`。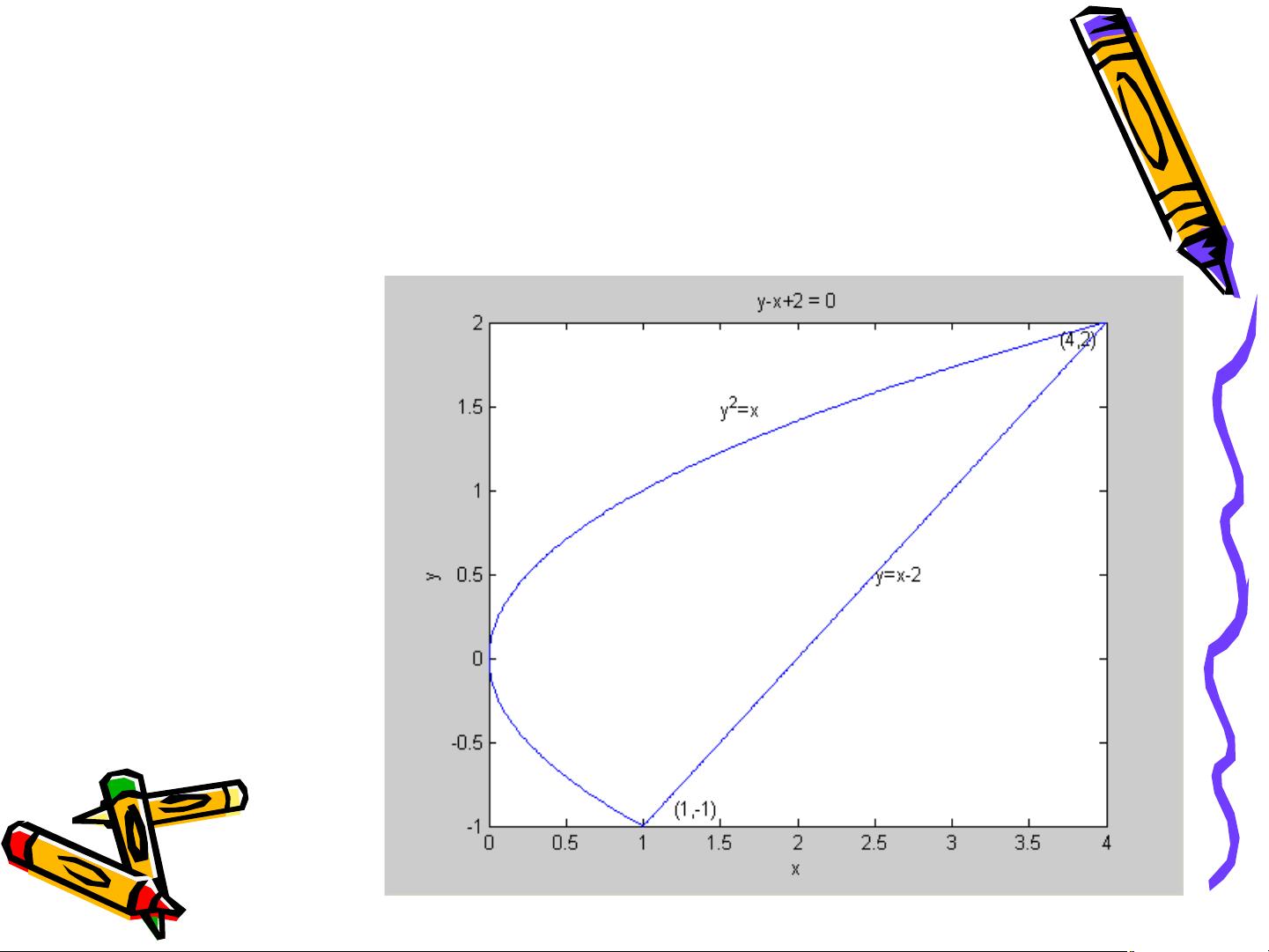 实验还涉及了在Matlab中如何处理实际应用问题。例如，通过求解两个方程的交点确定积分区域，然后使用`ezplot`函数绘制函数图形，结合`holdon`和`holdoff`控制图形叠加，最后进行积分计算。在例2中，计算由抛物线`y^2=x`和直线`y=x-2`围成的闭区域的积分，分别采用两种方法计算，结果都是`45/8`，这展示了积分顺序的不敏感性。 此外，虽然没有在提供的部分内容中直接提到，但三重积分是扩展到三维空间的积分，用于计算体积、质量、密度等。在Matlab中，三重积分同样可以使用`int`函数进行，但需要三个变量的积分，通常涉及到三个坐标轴的变换。 这个Matlab实验旨在使新手能够熟练运用软件进行积分计算，理解不同坐标系下的积分转换，并解决实际问题。通过这些实践，学习者不仅能掌握基本的积分理论，还能提升其在数值计算方面的技能。