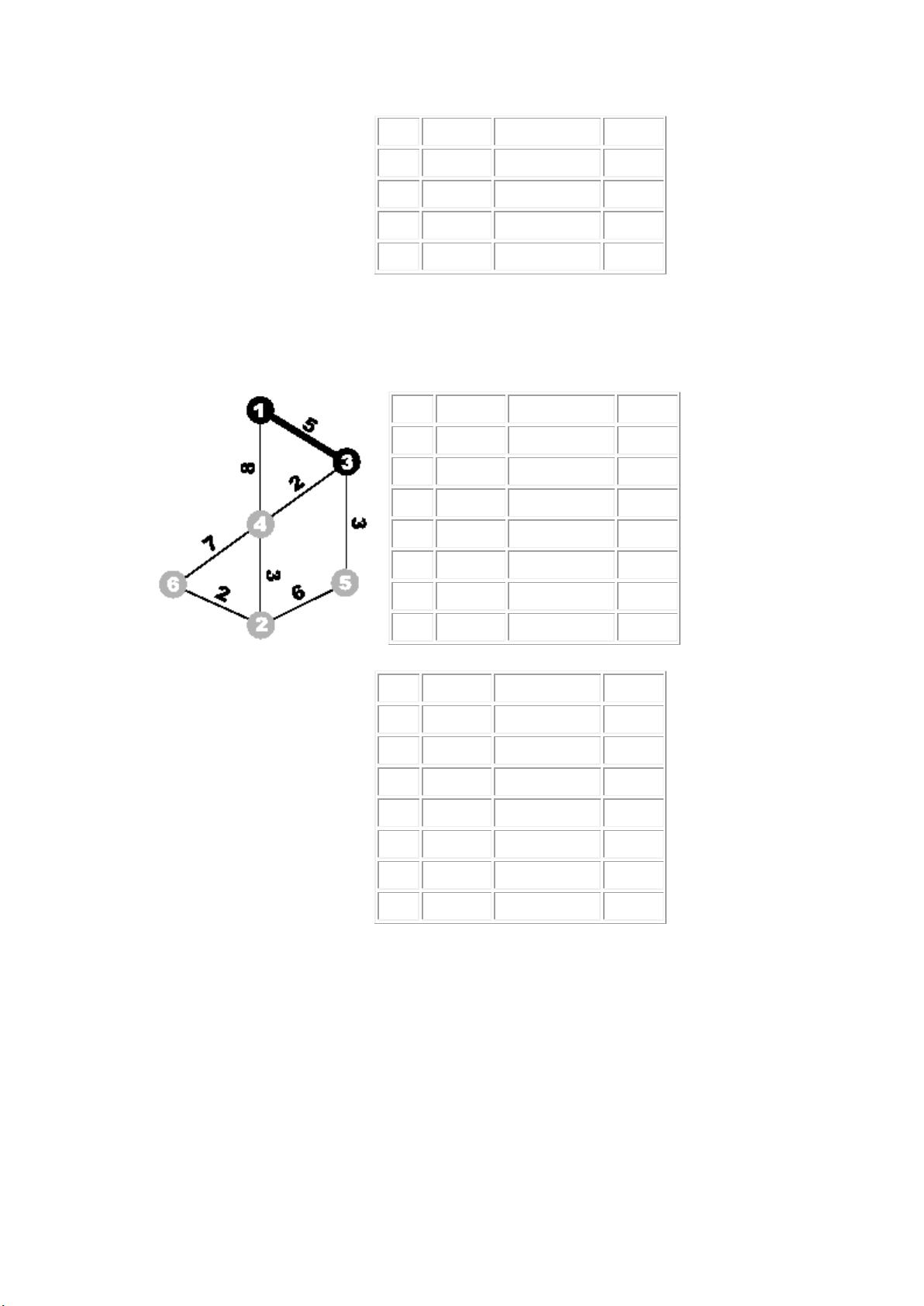
"解决最短路图论问题：过度围栏(Kolstad算例)"

Shortest Paths in Graph Theory One of the fundamental problems in graph theory is finding the shortest path between two points in a graph. This problem has numerous real-world applications, such as finding the quickest route for a delivery truck, the shortest path for a network packet to reach its destination, or the most efficient way for a robot to navigate a maze. There are several algorithms that can be used to solve the shortest path problem, with Dijkstra's algorithm and Bellman-Ford algorithm being the most commonly used. Dijkstra's algorithm is a greedy algorithm that finds the shortest path from a single source node to all other nodes in the graph, while the Bellman-Ford algorithm can handle graphs with negative edge weights. An interesting sample problem that demonstrates the application of shortest paths in graph theory is the Overfencing problem. In this problem, a farmer wants to build a fence around his pasture to keep his cows from escaping. The farmer has a limited amount of fencing material, so he wants to build the fence with the shortest length possible while still enclosing the entire pasture. To solve the Overfencing problem using graph theory, we can represent the pasture as a grid where each cell represents a unit of the pasture, and the edges between cells represent possible fence boundaries. We can then use Dijkstra's algorithm to find the shortest path from one corner of the pasture to the opposite corner, which will give us the shortest fence length needed to enclose the entire pasture. By finding the shortest path in the pasture grid using Dijkstra's algorithm, the farmer can efficiently build the fence with the minimum amount of material required. This demonstrates how graph theory and shortest path algorithms can be used in practical scenarios to solve optimization problems and improve efficiency.