Excel方差分析详解:判断多组数据均值差异
"此资源是一个关于Excel方差分析的教程,旨在教授如何利用Excel进行数据分析,特别是针对多个组别数据比较的方差分析方法。"
在统计学中,方差分析(ANOVA,Analysis of Variance)是一种用于比较多个组别间平均值差异显著性的方法。在Excel中,我们可以运用内置的功能来进行方差分析,帮助我们确定不同分类变量(如上级、同事、下属)对连续变量(如信息传播程度)是否有显著影响。
在【例9.1】中,研究者想要了解信息来源(上级、同事、下属)是否对信息传播的效果有显著影响。他们收集了24个样本数据,每个信息来源都有8个观测值。首先,他们计算了每个组别的平均值,分别是上级的5.75,同事的5.5,以及下属的5.25。直观上,这三个平均值似乎有所差异,但为了确定这些差异是否由随机因素引起,或者说是信息来源的真实影响,我们需要一个统计测试。
传统的两总体均值检验(如t检验)无法直接应用于三个或更多总体的情况,因为进行多次独立检验(例如,每个两两比较)可能导致错误率的增加。为了解决这个问题,方差分析引入了一个更有效的方法,它通过分析总变异(total variation)和组内变异(within-group variation)以及组间变异(between-group variation)来评估差异的显著性。
方差分析的基本假设包括:
1. 各组内的数据应服从正态分布。
2. 各组的方差应相等,即方差齐性。
3. 数据是在各组之间独立抽取的。
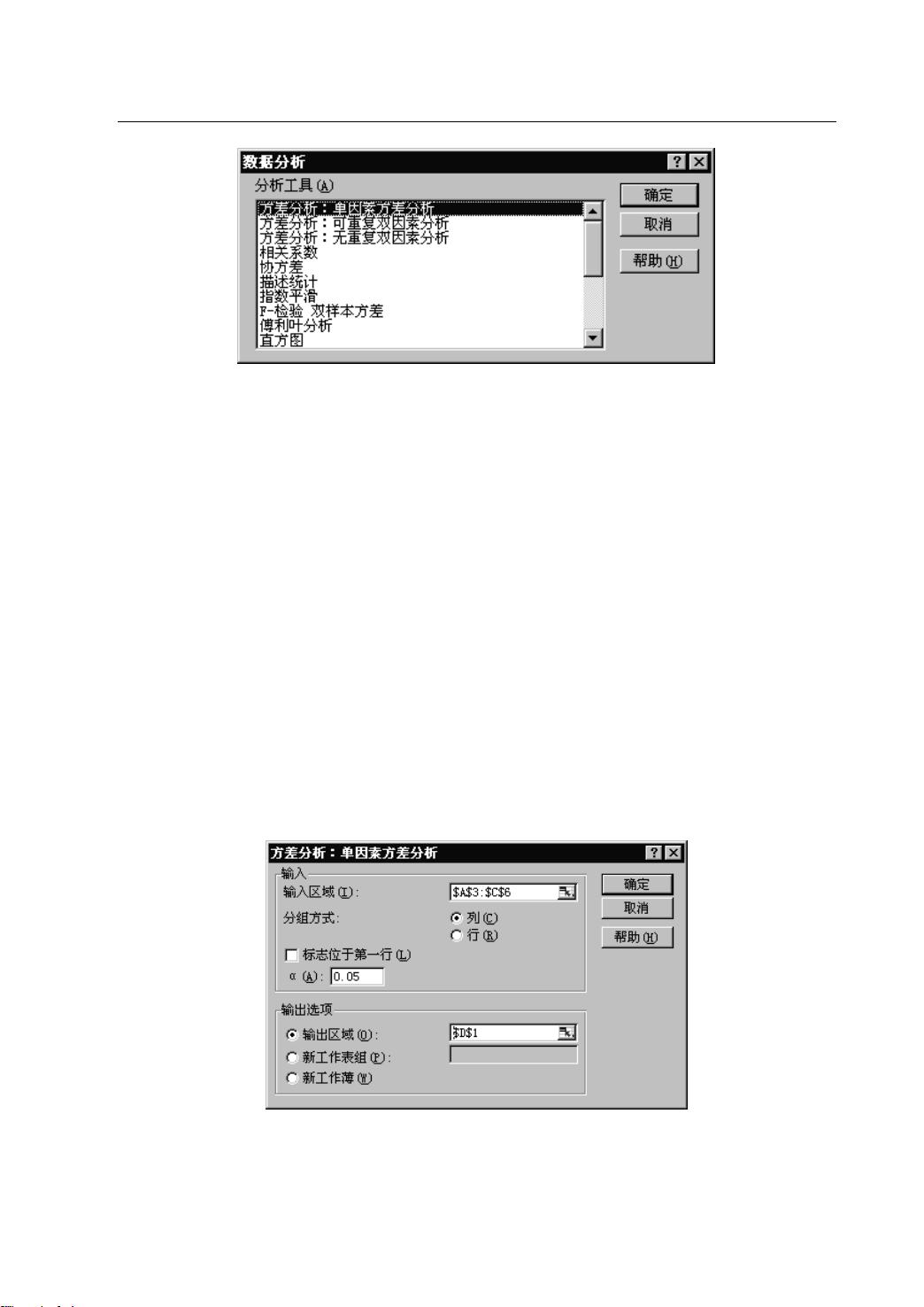
在Excel中,我们可以使用“数据分析”工具包中的“单因素ANOVA”来执行这个测试。输入数据后,Excel会计算出F统计量和对应的p值。F统计量是组间方差与组内方差的比例,而p值用于判断原假设(所有组平均值相等)是否应该被拒绝。
在【例9.1】的情况下,如果得到的p值小于显著性水平(例如α=0.05),则可以拒绝原假设,认为至少有一个信息来源的平均传播程度与其他来源显著不同。否则,我们不能拒绝原假设,意味着信息来源对传播程度的影响不显著,所有的平均值可能是由于随机误差造成的。
通过Excel的方差分析,我们可以更高效地处理多组比较的问题,避免了进行多次独立检验带来的多重比较问题。这使得研究人员能够更准确地理解和解释数据,从而做出更有依据的决策。
150 浏览量
2021-08-15 上传
162 浏览量
472 浏览量
tzzhuqi
- 粉丝: 0
最新资源
- 网狐工具:核心DLL和程序文件解析
- PortfolioCVphp - 展示JavaScript技能的个人作品集
- 手机归属地查询网站完整项目:HTML+PHP源码及数据集
- 昆仑通态MCGS通用版S7400父设备驱动包下载
- 手机QQ登录工具的压缩包内容解析
- Git基础学习仓库:掌握版本控制要点
- 3322动态域名更新器使用教程与下载
- iOS源码开发:温度转换应用简易教程
- 定制化用户登录页面模板设计指南
- SMAC电机在包装生产线应用的技术案例分析
- Silverlight 5实现COM组件调用无需OOB技术
- C#实现多功能画图板:画直线、矩形、圆等
- 深入探讨C#语言在WPF项目开发中的应用
- 新版2012109通用权限系统源码发布:多角色用户支持
- 计算机科学与工程系网站开发技术源码合集
- Java实现简易导出Excel工具的开发教程