Matlab实践：深度解析傅里叶变换与信号分析

在MATLAB实验中，主要关注的是傅里叶变换及其在周期信号分析中的应用。实验的核心目标是通过实践操作加深理解和掌握傅里叶级数的物理概念，以及如何利用MATLAB进行信号处理和频谱分析。具体来说，实验分为以下几个关键环节： 1. **实验目的**： - **周期信号傅里叶级数与频谱分析**：学习如何使用MATLAB实现周期信号的傅里叶级数展开，理解其背后的物理含义，如不同信号成分在频域的表示。通过实际操作，掌握如何绘制幅度谱和相位谱，从而分析信号的频率特性。 - **信号傅里叶变换**：掌握连续时间信号的傅里叶变换计算方法，包括使用符号运算和数值计算两种方式。理解傅里叶变换的性质，例如幅值和相位信息。 - **抽样定理验证**：学习信号的抽样过程，并利用MATLAB模拟，探究抽样频率对信号频谱的影响，验证抽样定理。 2. **实验原理及实例**： - **周期信号处理**：基于实验参考资料的特定章节，深入理解MATLAB如何处理周期信号的傅里叶级数展开和频谱分析，提供实例以便于理解和实践。 - **傅里叶变换性质**：介绍傅里叶变换的基本理论，包括如何运用MATLAB工具解析信号的频谱特征。 - **信号抽样**：详细解释抽样定理，通过MATLAB模拟信号抽样过程，观察不同抽样间隔下的频谱变化。 3. 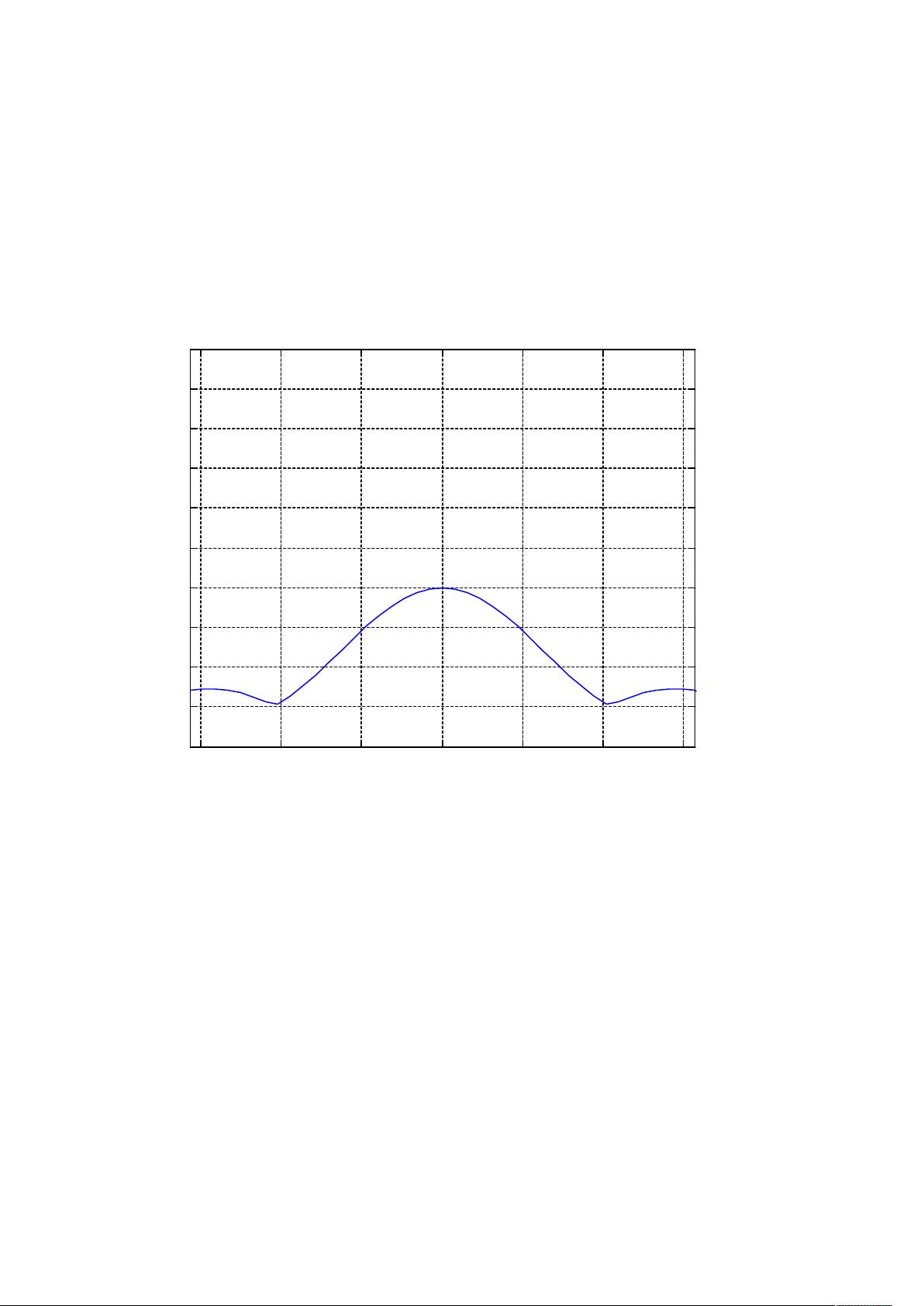**实验过程**： - **具体任务**：学生被要求用MATLAB求解给定的信号的傅里叶变换，首先使用符号运算方法，通过`sym()`函数和`fourier()`函数计算符号级的傅立叶变换，然后绘制幅度谱和相位谱。接着，使用数值计算方法处理同一信号，通过定义时间步长`dt`和采样点`t`，计算并可视化频谱图。 通过这个实验，参与者将不仅增强对傅里叶变换的理解，还会提升使用MATLAB进行信号处理和分析的技能，这对于理解复杂信号的频域特性以及数字信号处理基础至关重要。同时，通过实际操作和理论结合，可以巩固信号分析的基本概念，为后续深入研究或实际工程应用打下坚实基础。