电机FOC控制详解：坐标变换与C语言实现

"电机FOC中的坐标变换涉及关键步骤，包括CLARK变换和PARK变换，用于将三相交流电机的电流从原始的a、b、c相坐标系转换为直流等效的d、q坐标系，以实现更精确的磁场定向控制。CLARK变换将三相电流转换为两相静止的α、β坐标系，而PARK变换则进一步将α、β坐标系转换为旋转的d、q坐标系，与电机的磁场同步。在等幅值转换中，K取1，转换后各相电流幅值保持不变；在等功率转换中，K取√3/2，确保功率守恒。MATLAB/SIMULINK的仿真模型展示了这两种变换的过程和结果，对于理解和验证坐标变换的正确性具有重要意义。在实际应用中，等幅值变换通常用于避免过调制问题。PARK变换的矩阵表达式中，夹角θ代表d轴与α轴的夹角，确保了转换的准确性。" 电机控制领域的磁场定向控制（FOC）是一种先进的调速方法，它利用坐标变换来改善电机性能。FOC控制策略的核心是SVPWM、坐标变换、信号采集反馈以及PID闭环控制，其中坐标变换是连接电气和机械量的关键桥梁。 CLARK变换，也称为克拉克变换，将三相交流电流a、b、c转换为两相静止的α、β坐标系。该变换通过一个简单的线性矩阵完成，使得三相电流可以被直观地理解为在直轴和交轴上的分量。CLARK变换的逆变换则用于将α、β坐标系的电流转换回a、b、c相。转换系数K的选择可以根据需要进行调整，K=1对应等幅值转换，K=√3/2对应等功率转换。 PARK变换，又称帕克变换，是电机控制中另一个重要的步骤。它将静止的α、β坐标系进一步转换为旋转的d、q坐标系，其中d轴与电机的磁链方向对齐，q轴则与转速同步。这一变换使得电机的交流性质可以转化为直流性质，便于实现磁场定向和PID控制。PARK变换的矩阵包含了角度θ，该角度代表电机的磁场角度，确保了坐标系与电机实际状态的一致性。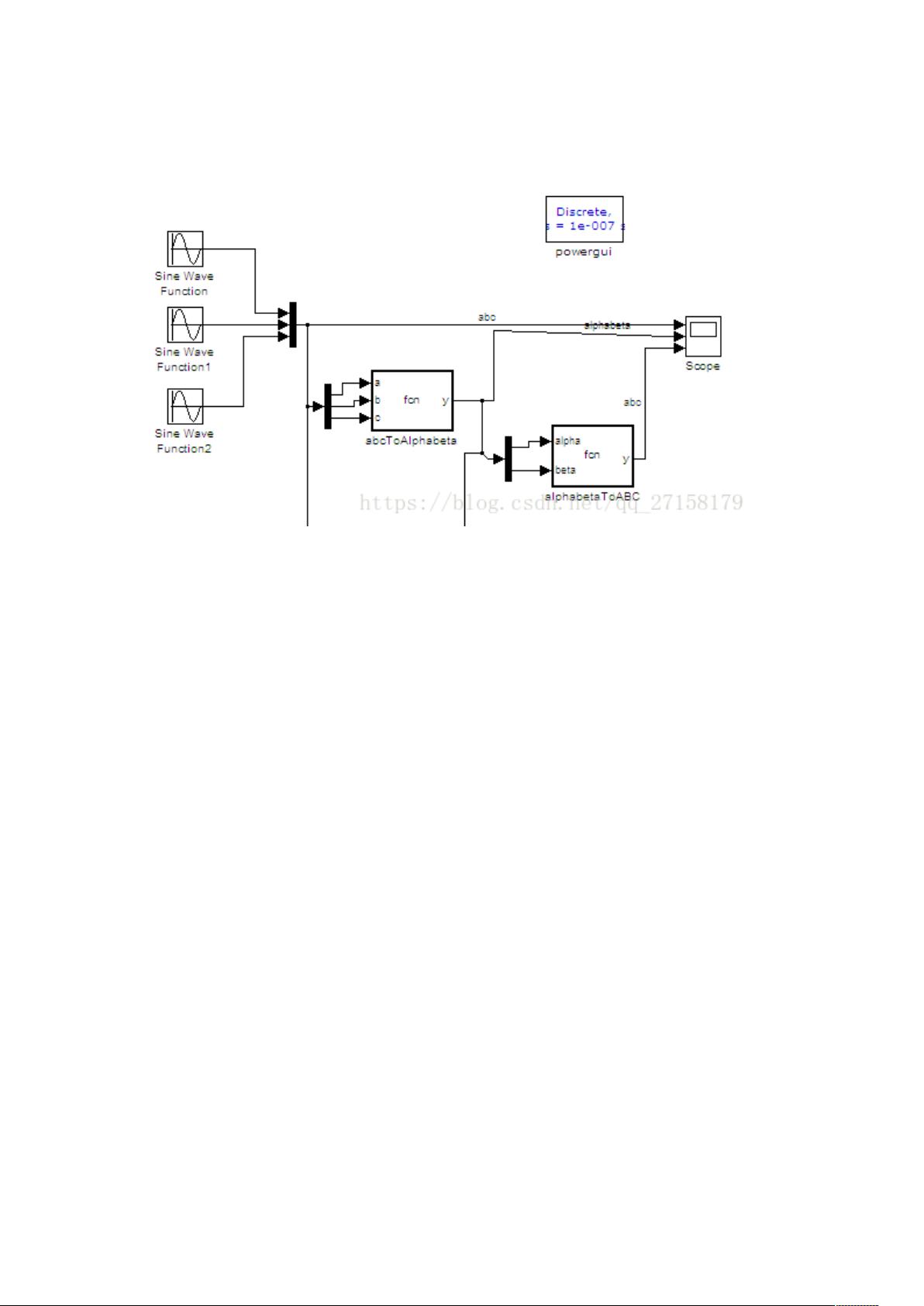 MATLAB/SIMULINK的仿真模型是验证这些理论的重要工具，通过建立abcToAlphabeta和alphabetaToABC模块，可以直观地观察不同变换的效果，如等幅值变换和等功率变换下的电流波形。等幅值变换通常在实际应用中更为常见，因为它避免了过调制问题，保证了SVPWM的效率和稳定性。 电机FOC中的坐标变换是实现精确电机控制的基础，它将复杂的三相交流系统简化为易于控制的直流系统，为优化电机性能提供了可能。通过深入理解并应用CLARK和PARK变换，工程师可以设计出更高效、更稳定的电机控制系统。