三角函数在三角形中的应用与公式总结

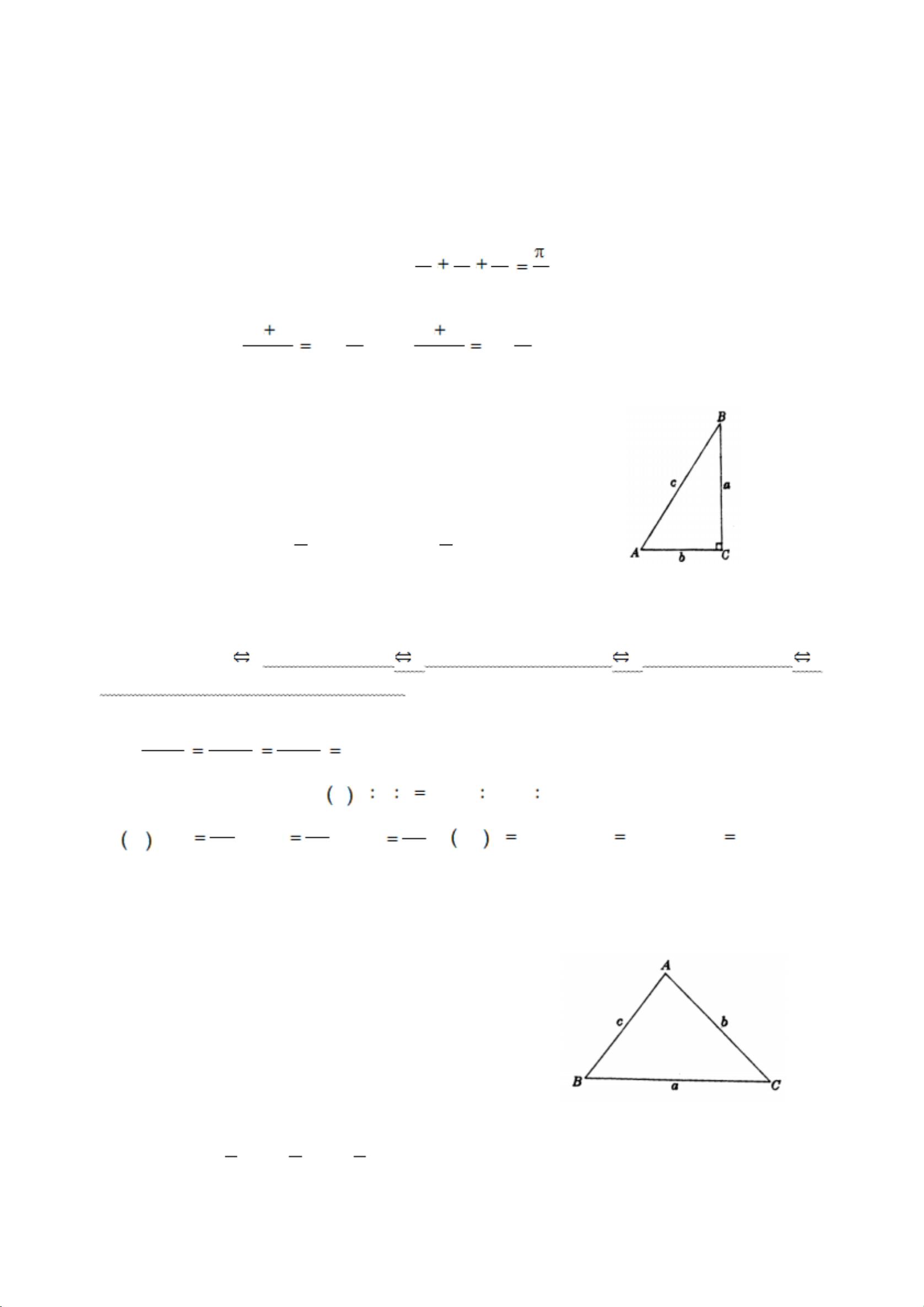
"3.三角形中的三角函数讲义.pdf" 这篇讲义主要涵盖了三角形中的基本概念和重要定理，特别是与三角函数相关的知识。三角函数是解析几何、微积分以及许多工程和物理问题中的核心工具。以下是具体内容的详细解释： 1. **边与角的关系**： - 边的关系：在任意三角形ΔABC中，任意两边之和大于第三边，即a + b > c；同时，任意一边小于另外两边之和，即a - b < c。 - 勾股定理：在直角三角形中，直角边a和b的平方和等于斜边c的平方，即a² + b² = c²。 2. **角的关系**： - 三角形内角和：所有内角的度数总和为180°，即A + B + C = π（弧度制中为π）。 - 角的互补和互余：两个角的和为90°，那么它们互为余角，如sin(A + B) = sinC；如果两个角的和为180°，它们互为补角，cos(A + B) = -cosC。 3. **边与角之间的关系**： - 直角三角形中，锐角三角函数定义了边与角的关系：sinA = cosB = c/a，cosA = sinB = c/b。 - 斜三角形中，不仅有锐角三角形的特性，还包括了正弦定理和余弦定理： - 正弦定理：对于任意三角形，各边与其对应角的正弦之比相等，且与外接圆半径有关，即a/sinA = b/sinB = c/sinC。 - 余弦定理：三角形中任意一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积，例如a² = b² + c² - 2bc·cosA。 - 射影定理：给出了三角形边长与夹角余弦的关系，如a = b·cosC + c·cosB。 4. **三角形的面积公式**： - 传统的面积公式：面积Δ = 1/2 * 底*高，对于三角形，可以表示为Δ = 1/2 * a*h_a = 1/2 * b*h_b = 1/2 * c*h_c，其中h_a、h_b、h_c分别是对应边上的高。 5. **解三角形的问题**： - 当已知三角形的两边和一个角时，利用正弦定理可能有两解，因为角度的选取有正负两种情况。 这些基本知识构成了三角函数的基础，对于解决涉及角度、长度和形状的问题至关重要。掌握这些概念和定理，有助于理解和解决各种数学和实际问题。