"混沌电路实验与同步控制研究：非线性特性与费根鲍姆常数"

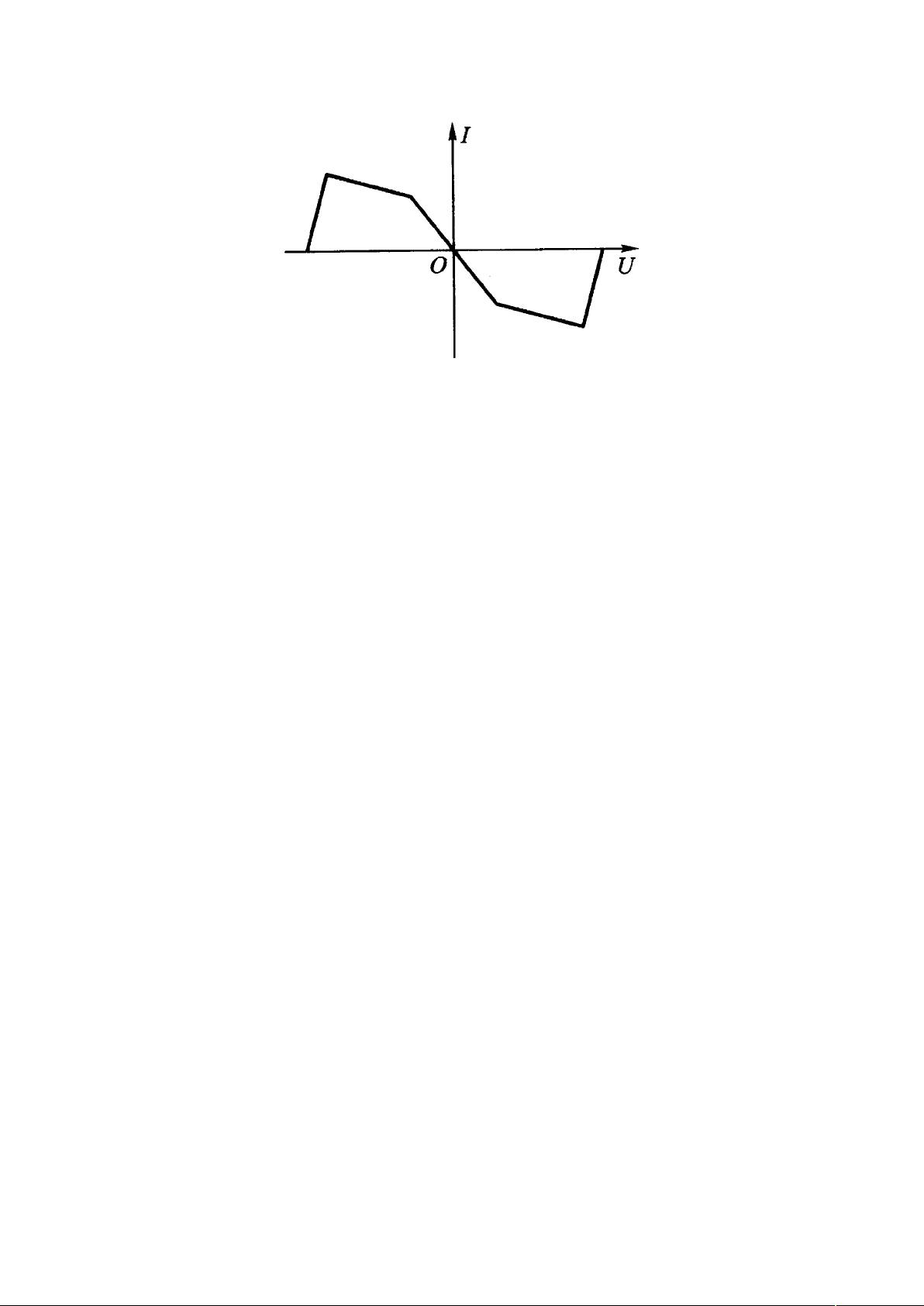
本实验报告通过测量非线性电阻的 I-U 特性曲线，了解非线性电阻特性，并搭建出典型的非线性电路——蔡氏振荡电路。通过改变其状态参数，观察到混沌的产生，周期运动，倍周期与分岔，点吸引子，双吸引子，环吸引子，周期窗口的物理图像，并研究其费根鲍姆常数。最后，实验将两个蔡氏电路通过一个单相耦合系统连接，并研究其混沌同步现象。混沌现象、有源非线性负阻、蔡氏电路、混沌同步、费根鲍姆常数是本实验的关键词。 1963年，美国气象学家洛伦茨在"确定论非周期流"一文中，给出了描述大气湍流的洛伦茨方程，并提出了著名的“蝴蝶效应”。这一发现揭开了对非线性科学深入研究的序幕。非线性科学被誉为继相对论和量子力学之后，20世纪物理学的“第三次重大革命”。由非线性科学所引起的对确定论和随机论、有序和无序、偶然性与必然性等问题进行了深入研究。 通过本实验的数据和观察，我们发现非线性电路混沌的产生可能与状态参数的改变有关。除此之外，我们还观察到了周期运动、倍周期与分岔、点吸引子、双吸引子、环吸引子、周期窗口的物理图像，并对其费根鲍姆常数进行了研究。这些发现为混沌现象提供了更加深入的理解和解释，并有助于我们在工程技术领域的应用。 在混沌电路的同步控制方面，本实验进一步研究了两个蔡氏电路通过一个单相耦合系统连接，最终研究了混沌同步现象。这一研究对于控制系统中混沌信号的稳定性和同步控制具有重要意义，有助于在通信、生物医学和信息安全等领域的应用发展。 在这一实验中，我们不仅深入理解了非线性电路混沌及其同步控制的基本原理，同时也学到了实验的设计和操作技能。这对于我们的理论知识和实践能力的提升都具有重要意义。 总的来说，本实验报告详细介绍了非线性电路混沌及其同步控制的实验过程和观察结果，对混沌现象和同步控制原理进行了深入研究和分析，为相关领域的进一步研究和应用提供了重要参考。通过该实验，我们对非线性电路混沌及其同步控制有了更深入、更全面的理解，也为我们今后的学习和研究工作提供了宝贵的经验和启示。