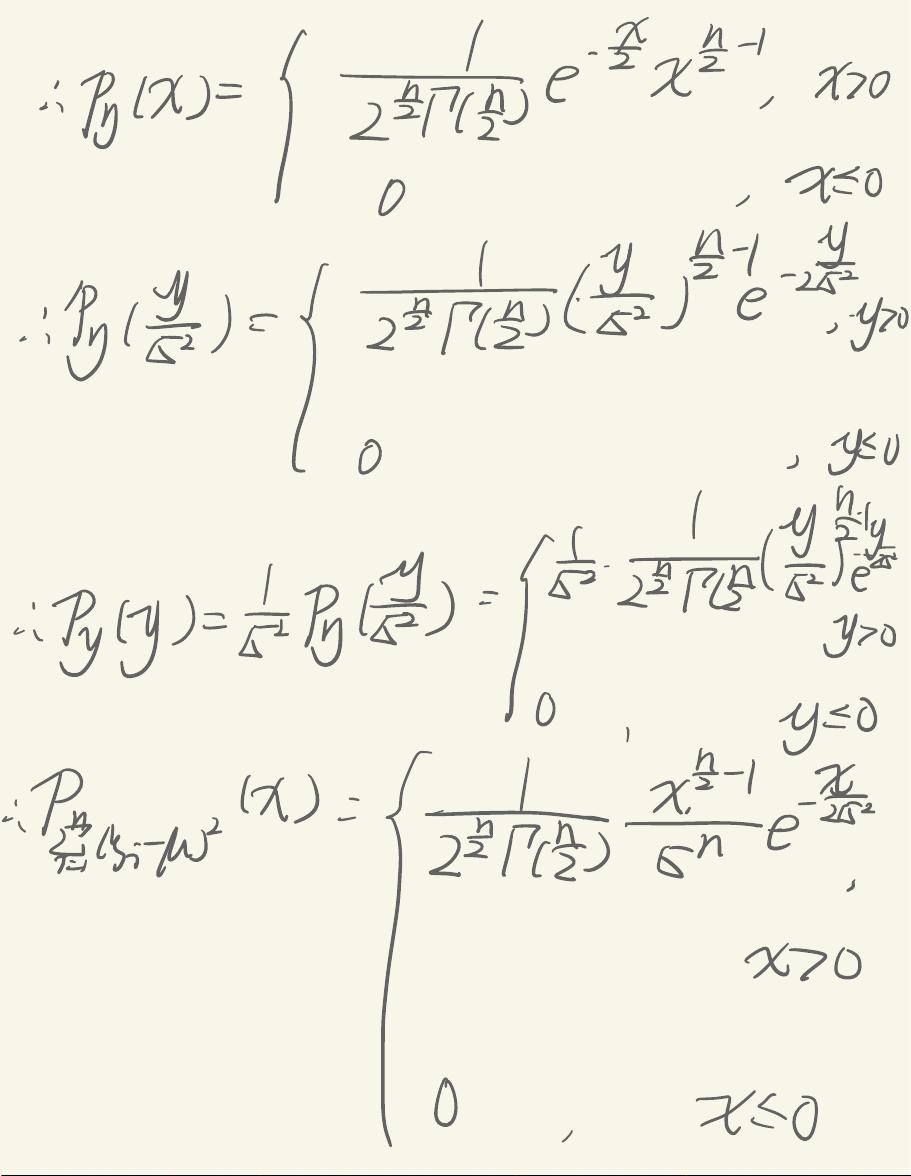华工工科数理统计期末复习关键点与习题解析
100 浏览量
更新于2024-06-26
1
收藏 130.13MB PDF 举报
"华南理工大学的工科数理统计期末复习资料,包含21个关键考点梳理,历年试题回顾,以及课后习题整理。复习材料是通过Goodnote软件制作的PDF文档,着重于数理统计的重要概念和方法,如抽样分布、矩估计、极大似然估计、中心极限定理、区间估计等。"
数理统计是统计学的一个分支,它涉及到数据的收集、分析、解释和呈现。在这个复习资料中,提到了以下几个重要的知识点:
1. **抽样分布**:当一个统计量基于随机样本计算时,该统计量的分布称为抽样分布。例如,样本均值的抽样分布,样本方差的抽样分布。理解抽样分布对于估计总体参数和进行假设检验至关重要。
2. **矩估计和极大似然估计**:矩估计是利用样本矩来估计未知参数的方法,而极大似然估计则是寻找使样本数据出现概率最大的参数估计值。两者都是参数估计的常用方法。
3. **中心极限定理**:在大样本情况下,不管总体分布是什么,样本均值的抽样分布接近正态分布,这是数理统计中的基本定理,对于理解样本统计量的行为极其重要。
4. **区间估计**:根据抽样结果,给出总体参数可能取值的区间,这个区间具有一定的概率覆盖总体参数。例如,95%置信水平下的置信区间。
5. **正态检验**:检验某个数据集是否符合正态分布,这对于理解数据的性质和后续的数据分析非常关键。
6. **方差分析**:用于比较两个或多个独立或相关样本的均值是否有显著差异,如单因素方差分析和有交互作用的两因素方差分析。
复习材料还强调了对概率论基础的理解,比如:
- **独立性和相关性**:独立事件的发生互不影响,而相关性则描述了两个变量之间的统计关联。
- **大数定律**:随着样本数量增加,样本均值趋向于总体均值。
- **分布函数和概率密度函数**:它们描述了随机变量的概率特性,例如期望和方差。
此外,资料特别提到了PPT中的例题和课本中的特定题目,这些都是复习的重点。例如,第二章强调了三大抽样分布(t分布,卡方分布,F分布)的应用,第三章的矩法估计和极大似然估计的练习题,第四章至第六章涉及的区间估计、正态检验和假设检验等。
这份复习资料覆盖了数理统计的核心概念和计算方法,旨在帮助学生全面掌握并准备期末考试。
430 浏览量
398 浏览量
145 浏览量
364 浏览量
430 浏览量
2024-03-15 上传
112 浏览量
110 浏览量
398 浏览量
xiaobai_Ry
- 粉丝: 2w+

最新资源
- Android客户端源码教程及下载指南
- Phoenix服务器启动指南与Elixir项目构建教程
- VMware ESX手册:iSCSI存储与VMware HA配置指南
- Android平台live555 20131018版本移植教程
- WinMend File Copy:80%时间优化的大文件快速复制解决方案
- Patran软件入门实例教程精讲
- Android Staggered Grid 布局示例与学习指南
- Winform实现折叠式导航菜单的设计与应用
- 个人简介:HTML技术专家
- WPF自定义颜色选择控件的设计与实现
- ExtJS3 窗口操作:修改后退出提示与直接退出的判断
- PB毕业设计完整版:图书管理系统开发指南
- 简易示波器的设计与应用
- 仿天猫App商品列表布局切换效果的实现
- 探索最强手指(TypingIt)源码与功能实现
- 基于JSP/Servlet和MySQL的动态信息发布平台开发