模式识别有监督分类:判别域代数界面方程法详解
“模式识别有监督分类PPT,涵盖了判别域代数界面方程法的基础知识,包括线性判别函数、二次准则函数等。”
在模式识别领域,有监督分类是一种广泛应用的技术,它依赖于已知的训练数据来构建分类模型。这份PPT主要讲解了判别域代数界面方程法,这是实现有监督分类的一种方法。
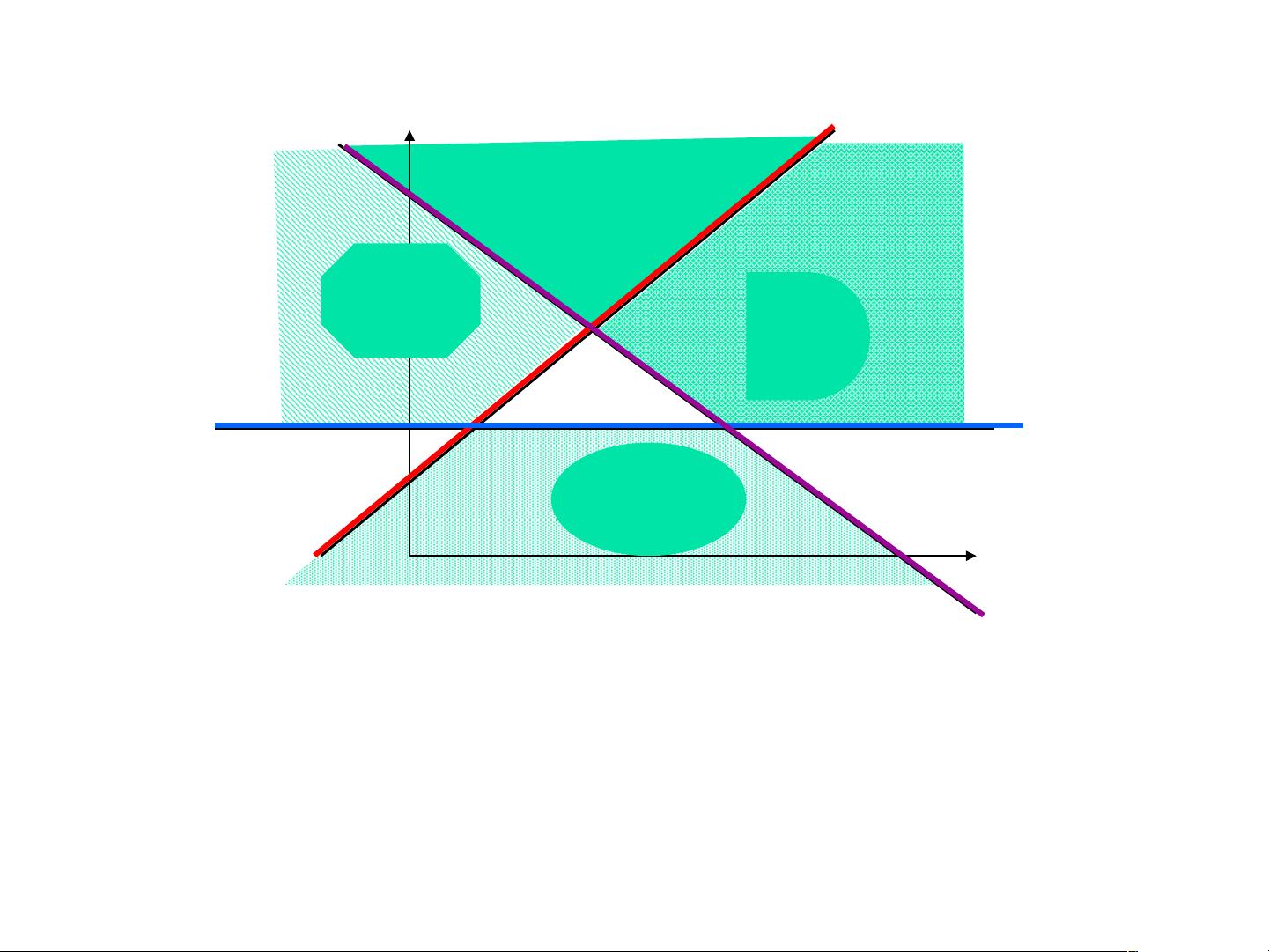
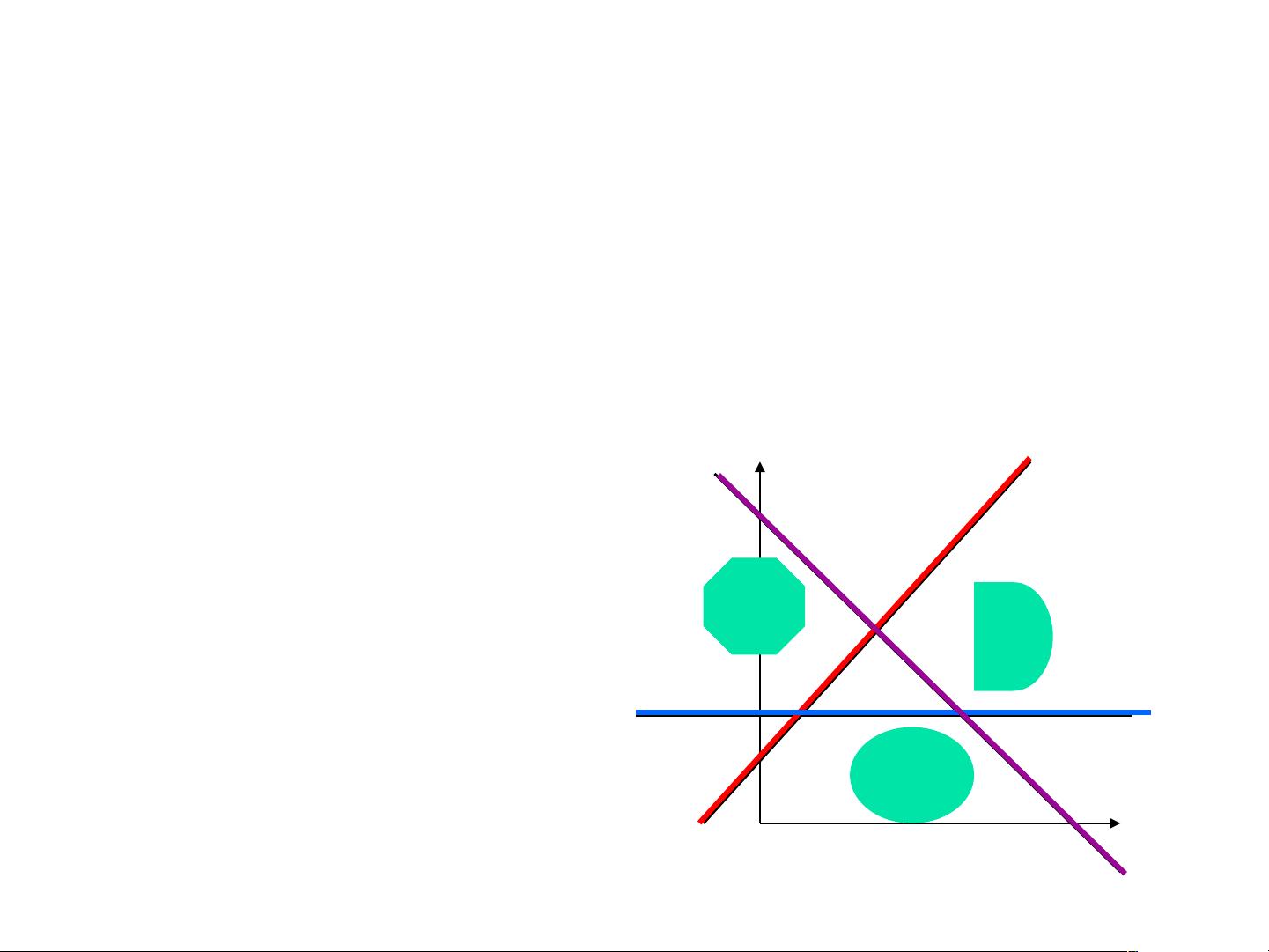
1. 判别域界面方程分类的概念:在模式识别中,我们的目标是通过分析特征来区分不同的类别。判别域界面方程分类法就是寻找一个边界或决策面,使得各类别的样本能够被有效地划分。这个边界通常表现为一个或多个方程,例如线性或非线性的判别函数。
2. 线性判别函数:在两类别问题中,线性判别函数是用于区分两类样本的线性表达式。如PPT中的例子所示,当两个类别的样本可以通过一条直线清晰地分开时,可以使用线性判别函数来找到这条最佳分离线。对于多类别问题,可能需要更复杂的线性组合来定义判别界面。
3. 判别函数的鉴别意义、权空间及解空间:判别函数的值可以帮助我们判断一个样本属于哪个类别。权空间指的是判别函数中权重参数的集合,而解空间则是所有可能的决策面构成的空间。通过对权重的调整,可以在解空间中找到最佳的分类边界。
4. Fisher线性判别:Fisher线性判别是一种经典的方法,旨在找到一个线性变换,使得类别间的方差最大化,同时类别内的方差最小化。这种方法通常用于高维数据降维,以便进行有效的分类。
5. 一次准则函数及梯度下降法:一次准则函数是用于优化判别函数的一种手段,通常与梯度下降法结合使用,通过迭代更新权重参数来最小化误差,从而找到最优分类界面。
6. 二次准则函数及其解法:在某些情况下,线性判别函数可能不足以描述复杂的数据分布,此时可以引入二次判别函数,如Quadratic Discriminant Analysis (QDA)。这类函数能更好地适应非线性边界,其求解通常涉及矩阵运算和特征分解。
7. 广义线性判别函数和位势函数分类法:这些是扩展了基本线性判别思想的更一般化的框架,可以处理更广泛的分类问题,如非线性或非高斯分布的样本。
通过深入学习这些概念和方法,我们可以理解和构建有效的有监督分类模型,应用于各种实际问题,如图像识别、自然语言处理和信号处理等领域。理解并掌握判别域代数界面方程法是模式识别和机器学习中的关键技能。
3227 浏览量
114 浏览量
2022-09-22 上传
2021-10-08 上传
2021-10-08 上传
2021-10-05 上传
150 浏览量
fyw1219
- 粉丝: 0
最新资源
- Ruby语言集成Mandrill API的gem开发
- 开源嵌入式qt软键盘SYSZUXpinyin可移植源代码
- Kinect2.0实现高清面部特征精确对齐技术
- React与GitHub Jobs API整合的就业搜索应用
- MATLAB傅里叶变换函数应用实例分析
- 探索鼠标悬停特效的实现与应用
- 工行捷德U盾64位驱动程序安装指南
- Apache与Tomcat整合集群配置教程
- 成为JavaScript英雄:掌握be-the-hero-master技巧
- 深入实践Java编程珠玑:第13章源代码解析
- Proficy Maintenance Gateway软件:实时维护策略助力业务变革
- HTML5图片上传与编辑控件的实现
- RTDS环境下电网STATCOM模型的应用与分析
- 掌握Matlab下偏微分方程的有限元方法解析
- Aop原理与示例程序解读
- projete大语言项目登陆页面设计与实现