图论定理：顶点度数之和与边数关系

"Sum of Degrees of Vertices Theorem是图论中的一个重要定理，它表明在一个有n个顶点的图中，所有顶点度数之和（记作Dv，即d1 + d2 + d3 + ... + dn）等于边的数量的两倍，即Dv = 2e。这个定理可以用中文表述为：在任何图形中，所有顶点的度数总和总是偶数。这个性质对于理解和计算图的结构非常有用。 举个例子，如果尝试构造一个有6个顶点的图，且顶点度数分别为1, 2, 2, 3, 3, 4，根据定理，我们预期的度数和Dv应为偶数，但实际计算Dv = 1 + 2 + 2 + 3 + 3 + 4 = 15，这是一个奇数，这说明这样的图并不存在，因为无法满足定理的要求。 在实际应用中，我们可以利用Sum of Degrees of Vertices Theorem来解决一些问题。例如： 1. 如果一个图有4个顶点，每个顶点的度数都是0，这意味着图中没有边，它是一个孤立点的集合或者称为无向图的空图。 2. 对于一个仅有一个顶点且度数为2的图，这个图必定是一个单点连通两个顶点的简单图。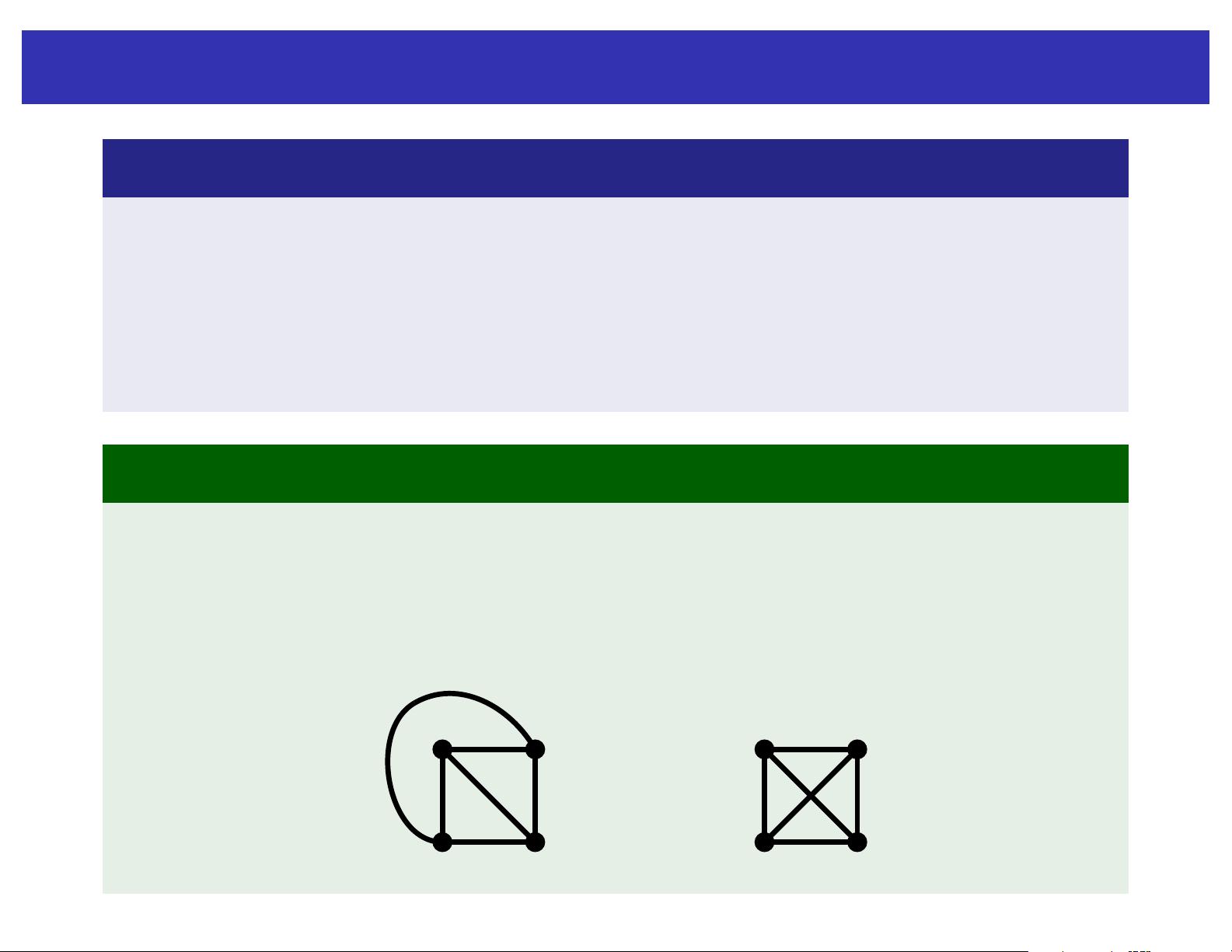 3. 当有4个顶点，度数分别为2, 3, 3, 和4时，由于Dv = 2e，我们可以推算出边的数量为(Dv/2) = (2 + 3 + 3 + 4)/2 = 4，所以图中有4条边，可能是环形或线性的结构。 4. 对于四个顶点的图，如果度数分布为2, 2, 2, 和4，虽然不能确定具体形状，但可以知道它不可能是完全无环图，至少存在一个循环，因为2 + 2 + 2 = 6，而每多一条边会使总和增加2，4条边足以形成一个循环。 Sum of Degrees of Vertices Theorem是图论基础中的基石，它提供了一种检查图是否合法以及预测其结构的方法。通过理解并运用这个定理，我们可以更好地分析和设计各种复杂的网络结构。"