环形拓扑多目标粒子群优化器：解决多模态多目标问题新方法

177 浏览量更新于2024-08-26 1 收藏 1.6MB PDF 举报

"使用环形拓扑的多目标粒子群优化器解决多模态多目标问题" 本文主要介绍了一种新的多目标粒子群优化器（MOPSO），该优化器针对具有多个帕累托最优解的多模态多目标优化问题进行设计。在多模态多目标问题中，可能存在多个帕累托最优解对应于相同的函数值。环形拓扑的概念被引入到粒子群优化算法中，以增强算法的稳定性，并帮助识别更多的帕累托最优解。传统的粒子群优化算法在处理多模态问题时可能会遇到困难，因为它们可能无法有效地探索和维护多样性的解集。为了解决这个问题，该论文提出了一种基于索引的环形拓扑结构。在这种结构中，粒子按照特定的顺序排列，形成一个循环网络，使得信息交换更加均匀，有助于发现更多局部最优解，从而增加找到全局最优解的概率。此外，为了评估决策空间和目标空间中的解分布质量，该方法采用了一种特殊的拥挤距离概念作为密度度量标准。拥挤距离是一种衡量解之间密度的方法，它可以帮助优化器在保持多样性的同时避免早熟收敛。通过调整这个度量，算法可以更好地平衡探索与开发，从而在决策空间和目标空间中获得更好的解分布。为了验证新算法的性能，作者们设计了新的多模态多目标优化测试函数，并提出了一个新颖的性能指标。这些测试函数旨在模拟实际问题的复杂性，而新的性能指标则用于更全面地评估算法在寻找并维持帕累托前沿的能力。通过与其他知名多目标优化算法的比较，研究证明了所提出的环形拓扑MOPSO在解决此类问题上的优越性。这篇研究论文为多模态多目标优化问题提供了一个有效的解决方案，通过创新的环形拓扑结构和拥挤距离策略，提高了算法在寻找和维持帕累托最优解集的效率和质量。这一工作对于多目标优化领域的理论研究和实际应用都具有重要的参考价值。

YUE et al.: MULTIOBJECTIVE PARTICLE SWARM OPTIMIZER USING RING TOPOLOGY FOR SOLVING MULTIMODAL MULTIOBJECTIVE PROBLEMS 807

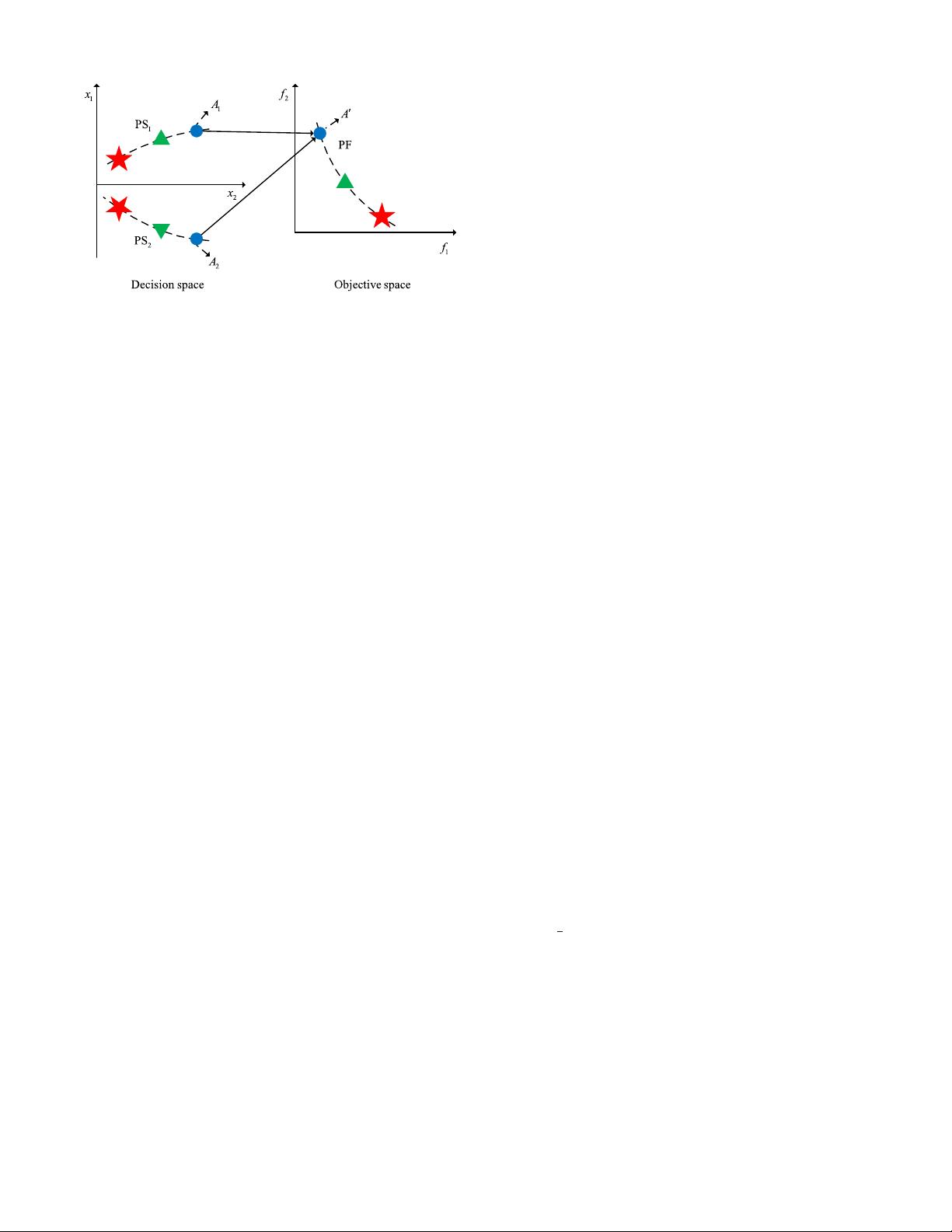
Fig. 2. Illustration of multimodal multiobjective problem.

approximate the PS and the PF. However, this algorithm can

only deal with multiobjective problems of class II [22]. Other

drawback of the method is the technique performs poorly when

the PS is a linear manifold.

Liang et al. [4] deﬁned the multimodal multiobjective

optimization problem, which could be succinctly illustrated

through the diagram in Fig. 2. The ﬁgure shows a simple

diagram illustrating a case, where there are two PSs cor-

responding to the same PF. Liang et al. [4] proposed an

algorithm called DN-NSGAII conceived for the purpose of

locating more PSs. The technique ﬁrst ranks solutions accord-

ing to nondominated sorting scheme and the solutions in

the same front are then sorted based on a decision-space

CD. Therefore, in DN-NSGAII the nondominated and less-

crowded solutions in the decision space are preferred. It has

been demonstrated that this algorithm can obtain more solu-

tions than NSGAII [23] and various other commonly used

multiobjective optimization approaches. However, the distri-

bution of solutions in the decision space is not very good (see

Fig. 9 (a) and (c) in [4]).

B. Framework of Particle Swarm Optimization

PSO is a population-based algorithm, which makes it par-

ticularly well suited for solving multimodal optimization

problems. PSO was inspired by the social behavior of birds

within a ﬂock [14]. In this method, the historical personal best

position of a point (also called particle) is denoted pbest, and

the historical best position of its neighborhood is called nbest.

Each particle in the swarm is led by pbest and nbest to ﬂy from

a starting position to a better area. Let x

(t) and v

(t) denote

the position and velocity of particle p

of the tth generation.

They are updated according to the following equations:

x

(t) =x

(t − 1) +v

(t) (4)

and

v

(t) = Wv

(t − 1) + C



x

pbest

−x

(t)



+ C



x

nbest

−x

(t)



(5)

where W is the inertia weight (often set to 0.7298, according

to [24]), C

and C

are constants (which satisfy the equal-

ity C

+ C

= 4.1[24]) used to balance exploration and

exploitation processes, and r

and r

are random values uni-

formly generated in the range [0, 1]. The key step in the

PSO methodology is the selection of leaders for the current

particles [25].

When extending PSO algorithms from the single-objective

to the multiobjective case, three issues become of particu-

lar signiﬁcance: 1) the selection of a leader particle; 2) the

management of the distribution properties; and 3) the man-

agement of the convergence speed. Regarding the ﬁrst issue,

the leader-particle selection is a relatively straightforward pro-

cedure in single-objective optimization, where one can simply

declare that particle with the largest ﬁtness value is the best

candidates to serve as leaders. In multiobjective optimization,

however, the identiﬁcation of a best leader among all the solu-

tions may become a challenging task due to inherent conﬂicts

introduced by the multiple objectives. In that case it is natu-

ral to give preference to nondominated solutions to serve as

candidates for the leader designation. Concerning the second

issue, it is necessary to develop of a methodology that can

ensure a good distribution of solutions in the decision space

and in the corresponding objective space. Finally, regarding

the third issue, the PSO convergence speed has been addressed

through a number of communication topologies. In particular,

the star, ring, and von Neumann topologies are known to be

effective in avoiding premature convergence. The topology-

based PSO algorithms are reviewed and compared in [26].

However, these topological approaches cannot induce stable

niches, and as a consequence in multimodal problems the

population converges to a single solution instead of multiple

solutions. In contrast, r3pso described in [12], which incor-

porates an index-based ring topology, has been demonstrated

through experimental results that it can form stable niches.

In addition, the algorithm does not require the introduction

of niching parameters, which is an attractive feature. The

three issues described here are addressed in the new algorithm

described in the next section.

III. D

ESCRIPTION OF MO_RING_PSO_SCD

As a population-based algorithm, PSO has the capability,

and hence the natural advantage of searching for multiple

optima in a single run. In multimodal multiobjective opti-

mization problems, where a large number of Pareto-optimal

solutions should be searched for and maintained, PSO is there-

fore a natural choice for use as an optimizer. Inspired by the

single-objective particle swarm optimizer using ring topology

proposed by Li [12], this paper proposes a multiobjective PSO

algorithm with ring topology, and includes a SCD, which the

authors denote by the acronym MO_Ring_PSO_SCD. In this

section, the

MO_Ring_PSO_SCD procedure is presented fol-

lowed by a discussion of its underlying mechanism for the

purpose of analyzing how and why the proposed algorithm

can successfully address multimodal multiobjective problems.

Finally, the novelty of the proposed algorithm is described

and the convergence behavior of MO_Ring_PSO_SCD is

compared with that of alternative algorithms.

A. Procedure of MO_Ring_PSO_SCD

In MO_Ring_PSO_SCD, the personal best archive (PBA)

and the neighborhood best archive (NBA) are ﬁrst estab-

lished, and then the pbest and gbest are selected from the two

respective archives. Ring topology is used to induce multiple

剩余12页未读，继续阅读

weixin_38651450

粉丝: 1

环形拓扑多目标粒子群优化器：解决多模态多目标问题新方法

形拓扑多模态多目标粒子群算法的代码

Python 构建并实现一种基于环形拓扑的多目标粒子群优化（mOPSO）算法（含完整的程序和代码详解）

用于跳频分量搜索的环形拓扑粒子群算法.pdf

多模态多目标群智能优化算法

昂贵优化问题，高维昂贵优化问题，多模态优化问题，大规模优化问题，动态多目标优化问题。描述这些问题的时候怎么进行过渡

多模态多目标发展趋势

粒子群算法优化变分模态分解

粒子群优化VMDmatlab

粒子群优化算法优化卡尔曼滤波器的matlab实现

在粒子群优化算法中，高斯变异与Levy飞行策略是如何结合使用的？这种结合能有效解决哪些优化问题？

最新资源