图的定义与术语解析：从有向图到连通图

"该资源是关于数据结构课程的第七章，主要讲解了图的概念和相关术语，包括有向图、无向图、完全图、稀疏图和稠密图的定义，子图的概念，以及带权图和网络的介绍。此外，还涵盖了路径、路径长度、简单路径和回路等概念，特别是连通图和非连通图的连通分量定义。" 在计算机科学中，数据结构是组织和管理数据的重要方式，而图作为一种复杂的数据结构，广泛应用于各种算法设计中，如路由算法、社交网络分析、任务调度等。本课件首先定义了图的基本元素：顶点（Vertex）和边（Edge），并区分了有向图和无向图。有向图的边具有方向性，从一个顶点指向另一个顶点，而无向图的边没有方向，表示两个顶点之间的双向关系。 接着，课件介绍了完全图的概念，无论无向还是有向，完全图意味着图中任意两个不同的顶点间都存在一条边。对于无向完全图，n个顶点会有n(n-1)/2条边，而有向完全图则有n(n-1)条边。 稀疏图和稠密图是根据边的数量相对于顶点数量来分类的。当边的数量远小于顶点数量的平方根乘以顶点数量时，我们称其为稀疏图；反之，如果边的数量接近或超过顶点数量的平方，那么这个图被认为是稠密图。 子图的概念指出，如果一个图的顶点集和边集都是原图的子集，那么这个图就是原图的一个子图。这一概念在图的简化或者部分分析时非常有用。 带权图是图的一个扩展，允许在边附加数值，这些数值通常代表某种意义，例如距离、成本或者权重。带权图在现实世界的问题中非常常见，如公路网络中计算最短路径，或通信网络中计算最小代价路径。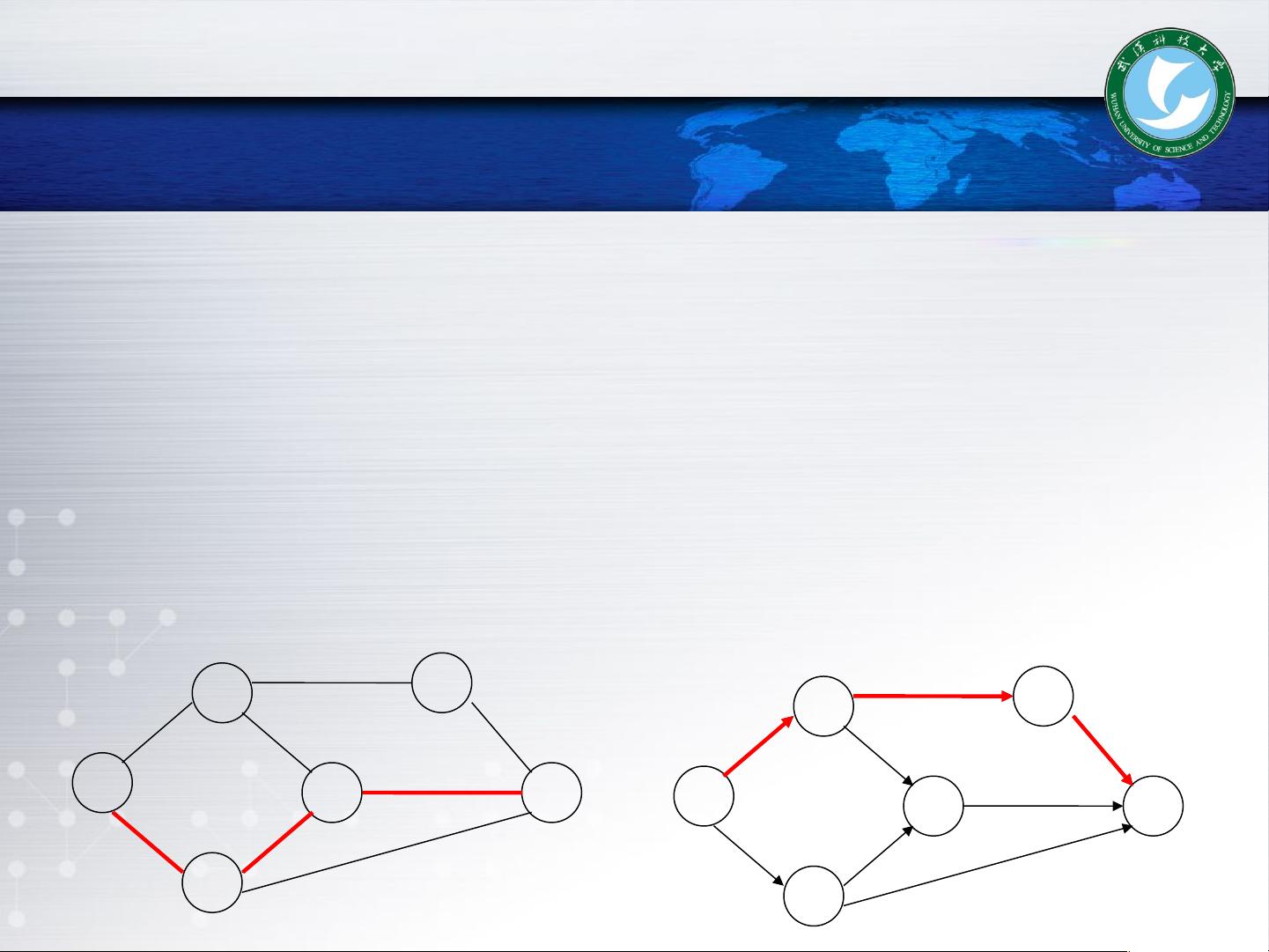 路径和回路是图中的重要概念。路径是从一个顶点到另一个顶点沿着边的序列，路径长度可以是边的数量或边的权重总和。简单路径是指路径上的顶点不重复，而回路或环则是路径的起点和终点相同的情况。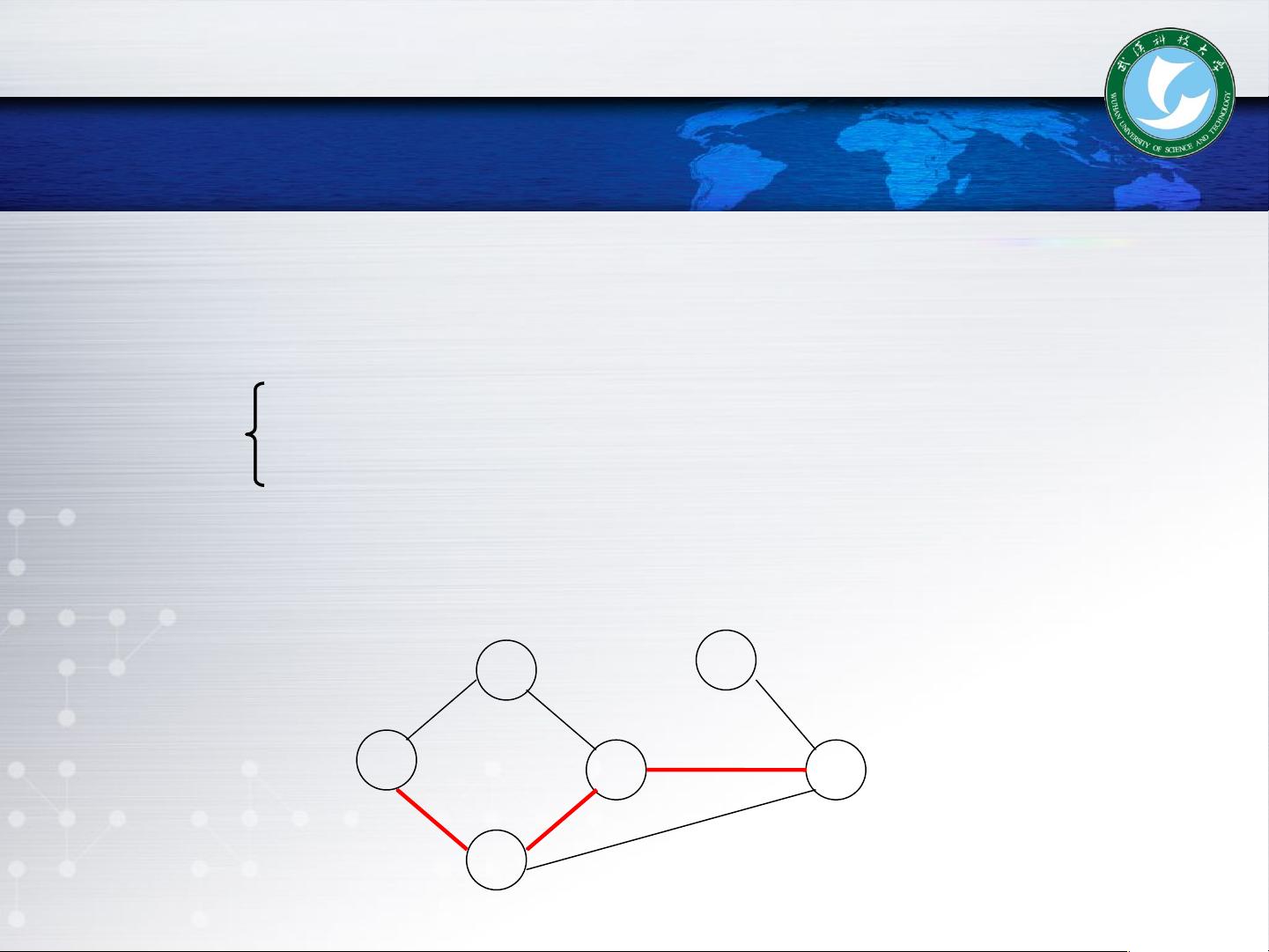 连通图是指图中任意两个顶点之间都存在路径，这意味着图是“连通”的。如果图中存在不连通的部分，那么最大的连通子图被称为连通分量，这是理解图的结构和进行图算法设计的关键概念。 这些基础概念构成了图论的基础，对于理解和操作图数据结构至关重要，是学习数据结构和算法的必经之路。