运算放大器应用详解：比例、加减、积分与微分运算

"运算放大器经典应用.pdf" 运算放大器是模拟电路中的核心元件，具有高增益、高输入阻抗、低输出阻抗等特性，广泛用于各种信号处理电路。本资料详细介绍了运算放大器在比例运算、加减运算、积分与微分运算以及对数和指数运算中的应用。 在比例运算电路中，分为反相和同相两种类型。反相比例电路通过电压并联负反馈实现，其特点是反相端为虚拟地，共模输入可以视为0，因此对运放的共模抑制比要求较低。输出电阻小，适合驱动大负载，但当需要大增益时，反馈电阻Rf的值会很高，可能导致系统稳定性下降。例如，若要实现100倍的放大，R1为100K欧姆，Rf则需设置为10兆欧姆。T型反馈网络也是反相比例电路的一种，同样利用了虚短和虚断的概念。 同相比例电路采用电压串联负反馈，输入端虚短，使得输入电阻非常高，输出电阻小，能有效驱动负载。由于输入端电压相同，对运放的共模抑制比有较高要求。电压跟随器是一种特殊形式的同相比例电路，它具有很高的输入阻抗和低输出阻抗，能够保持输入和输出信号的一致性，同时从信号源汲取的电流极小。 在加减运算电路中，反相求和电路允许独立调整各输入信号的比例，而不会影响其他输入到输出的比例关系。同相求和电路也有类似的特点，但所有输入信号都必须为同相。单运放和差电路可以实现简单的加法或减法运算，而双运放和差电路则可以同时处理多个输入信号，实现复杂的加减运算。例如，设计一个加减运算电路，Vo=2Vi1+5Vi2-10Vi3，可以通过适当选择反馈电阻和输入电阻来实现。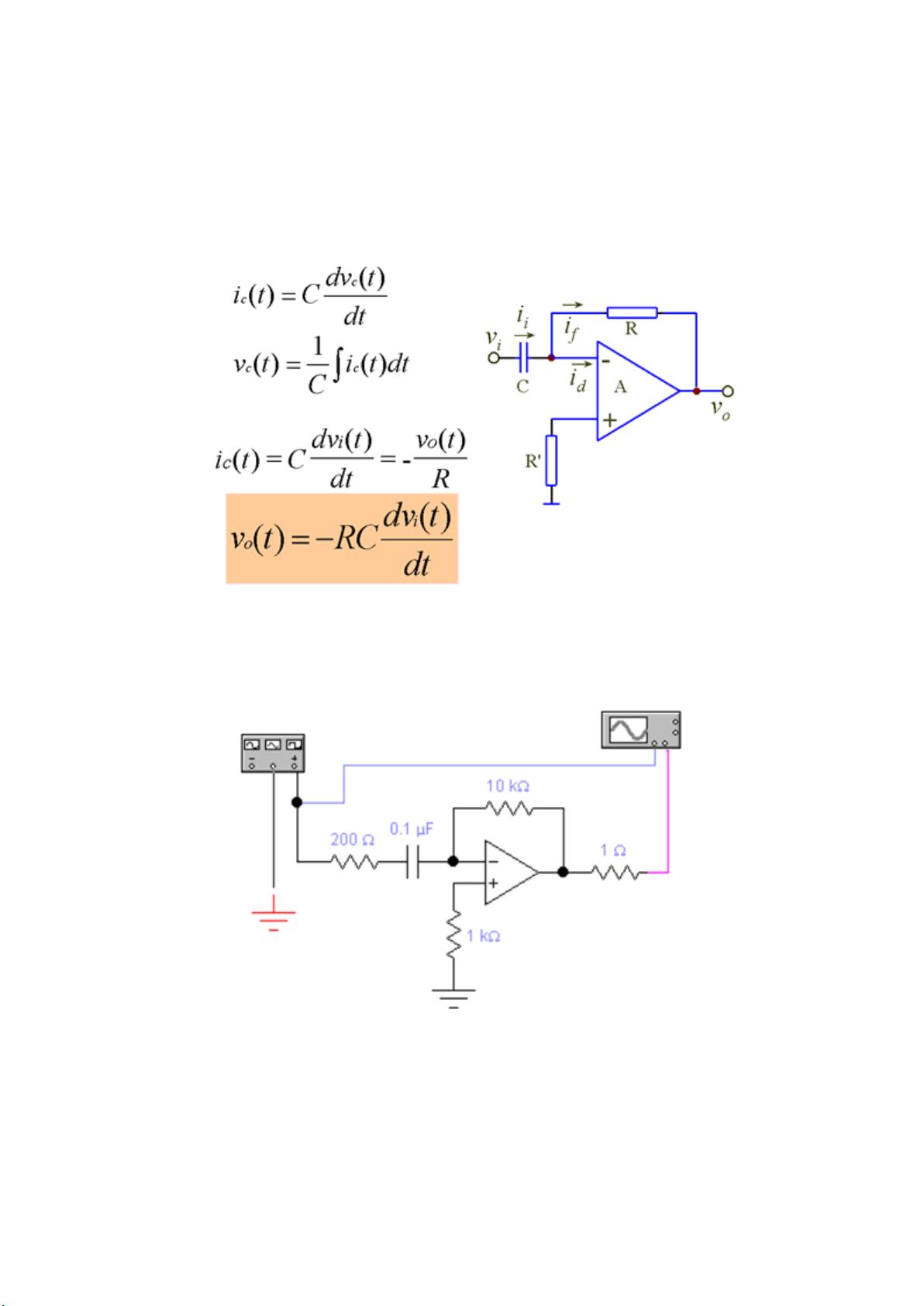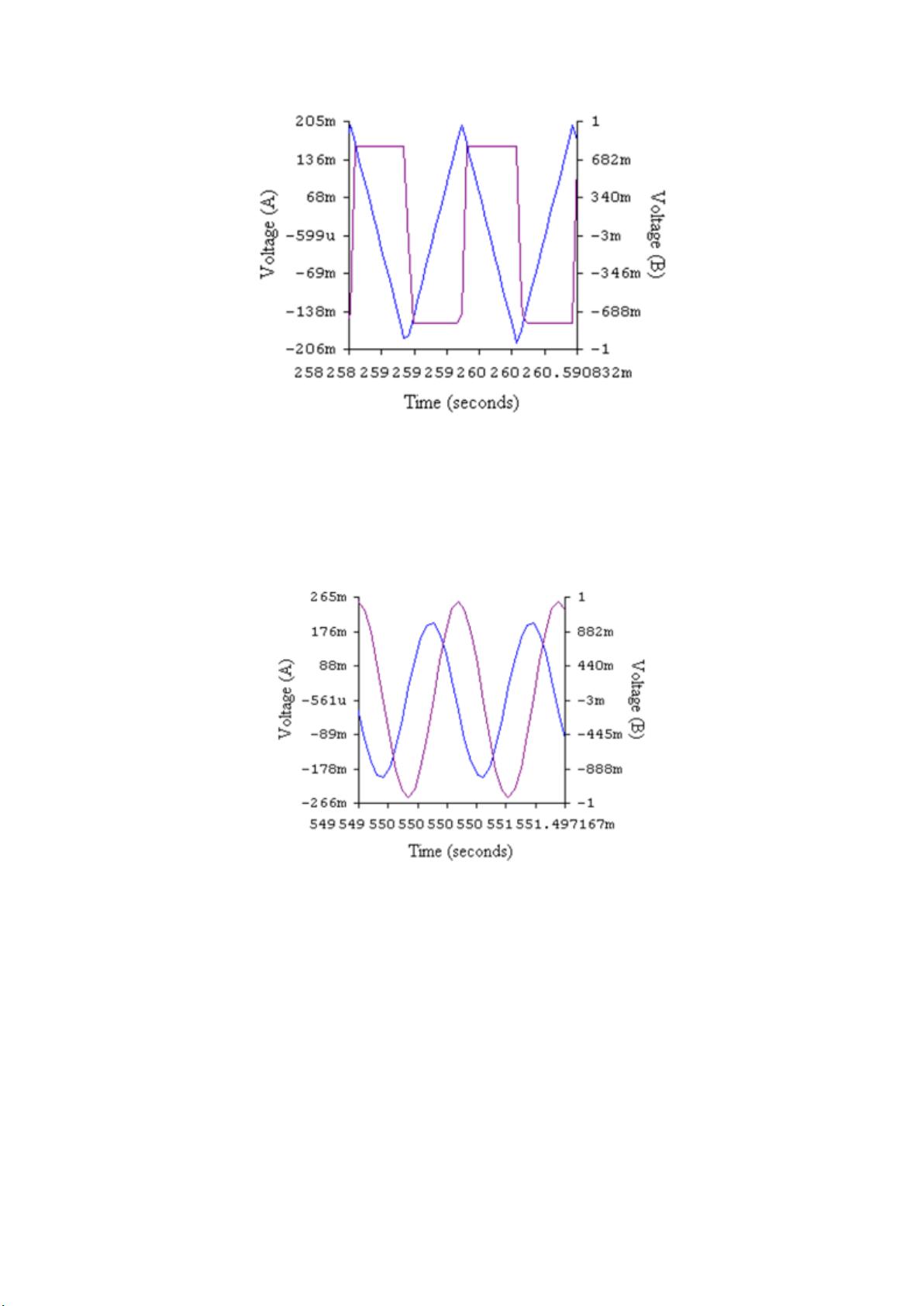 积分电路是运算放大器应用中的重要部分，其基本形式是电容和电阻的组合，能够将方波转换为三角波，或将三角波转换为正弦波。积分电路对于去除高频干扰、信号移相以及模数转换中的电压到时间转换都有重要作用。微分电路则相反，可以将三角波转换为方波，或者对方波进行相位响应分析。输入信号的频率对输出信号的幅度和相位有着直接影响。 对数和指数运算电路则利用运算放大器构建非线性特性，但基本对数电路可能受到温度影响，导致运算精度降低，因此通常需要改进设计来提高稳定性。 运算放大器的经典应用涵盖了信号处理的各个方面，从基本的电压放大到复杂的信号转换，是电子工程中不可或缺的一部分。通过理解这些基本电路，工程师可以设计出满足特定需求的电路系统。