无闭轨Lienard系统中α3β4与α3β6结构的实现与拓扑分析

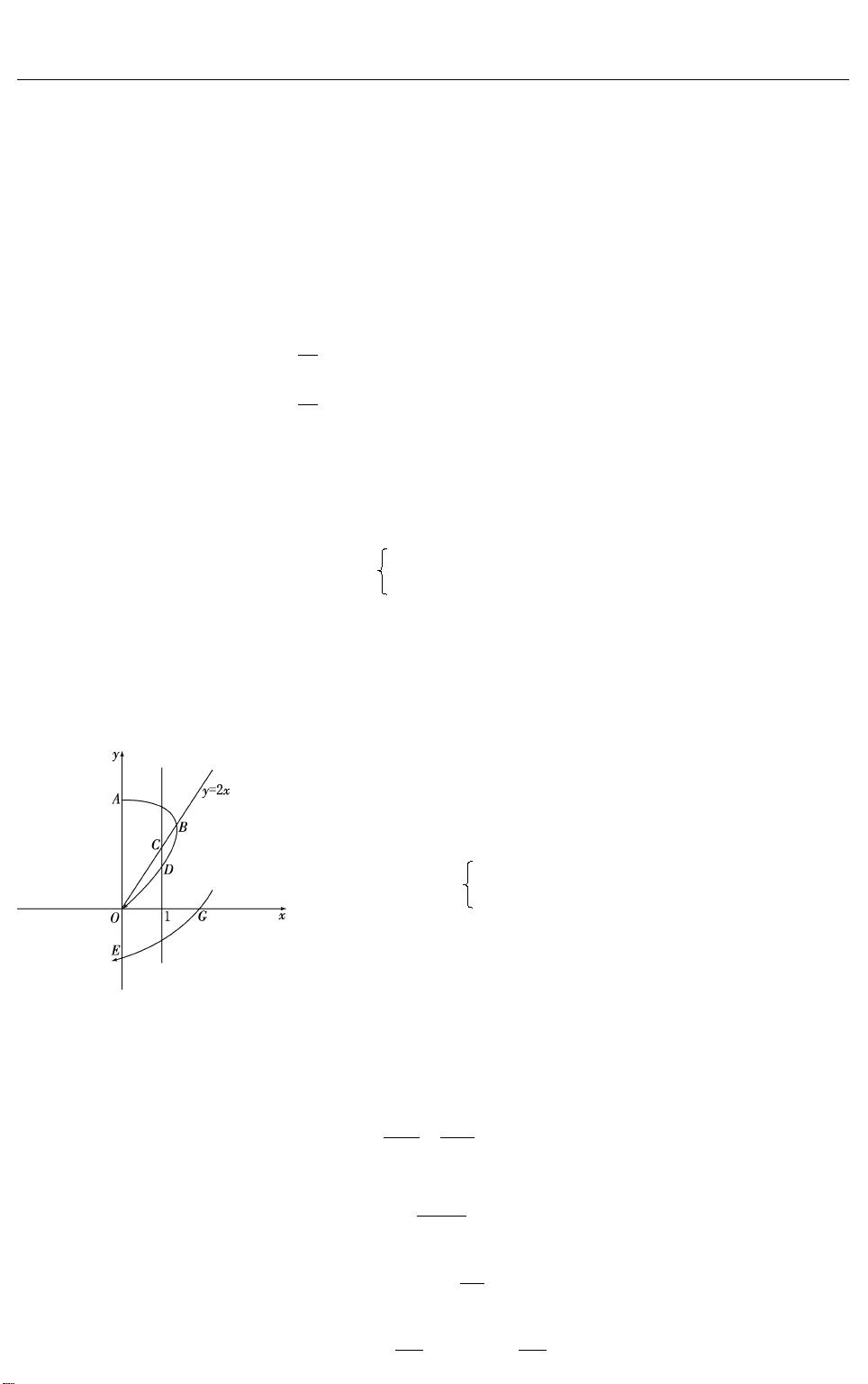
本文档主要探讨了无闭轨Lienard系统的拓扑分类问题，这是一种经典的二阶微分系统，广泛应用于医学、物理、机械和通讯等领域。Lienard系统的标准形式为x'' + f(x)x' + g(x) = 0，其中f和g是实数到实数的连续函数，且满足xg(x) > 0，当x不等于0时。 论文首先概述了Lienard系统的背景，指出它的重要性，例如vanderPol方程和与无线通信技术相关的方程，它们都是Lienard系统特定形式的例子。vanderPol方程是μ(x^2 - 1)x' + x = 0，常用于模型心脏跳动或电路反馈，而（3）中的方程则涉及到L，r和C这样的参数，是研究通信技术时的典型模型。 文章的核心部分是对72种完整的无闭轨Lienard系统拓扑结构进行深入分析。作者证明了其中与结构A+ B+ C+ D+ 0相对应的16种结构——α3β4-1至α3β4-4以及α3β6-1至α3β6-12——具备实现性。这是一项重要的贡献，因为这表明这些特定的拓扑结构不仅理论上存在，而且在实际应用中是可以构造和实现的。 作者给出了每一种可实现拓扑结构的充分条件，这是设计和分析这类系统稳定性、行为和控制策略的关键依据。这些条件可能涉及函数f和g的具体形式、参数选择、或者系统行为的特定边界条件。通过这些条件，研究者可以设计出符合实际需求的Lienard系统模型，并预测其动态性能。 此外，论文还提到了研究过程中使用的工具，如Gauss球面和Filippov变换，这些都是分析非线性系统动态行为的重要数学工具。Gauss球面用于处理系统在零点附近的局部行为，而Filippov变换则用于处理多值映射，适用于处理系统的不连续性。 总结来说，这篇文章不仅扩展了我们对无闭轨Lienard系统拓扑分类的理解，也为工程领域的实际应用提供了一套理论基础和设计指导。这对于推进动力系统理论研究和解决实际问题具有重要意义。