Matlab实例解析：多项式根与特征多项式计算

MATLAB是一种强大的数值计算软件，广泛应用于工程、科学和数据分析领域。本文档提供了一系列实用的MATLAB例题详解，重点围绕多项式根和特征多项式的求解，以及传递函数的分析。 首先，例1.4展示了如何利用MATLAB内置函数`roots`求解多项式`s6 + 9s5 + 31.25s4 + 61.25s3 + 67.75s2 + 14.75s + 15`的根。多项式系数以降幂次序排列存储在向量`P`中，通过`P=[1 9 31.25 61.25 67.75 14.75 15]`，然后调用`r=roots(P)`得到根的实部和虚部构成的列向量。结果显示了六个根，包括四个实根和两个复数根。 接着，在例1.5中，给出了复数根的处理方法。首先定义虚数单位`i=sqrt(-1)`，然后将根以行向量`r=[-1;-2;-3+4*i;-3-4*i]`的形式输入，通过`p=poly(r)`得到对应的多项式系数，从而求得多项式`s4 + 9s3 + 45s2 + 87s + 50 = 0`。 在更复杂的例1.6中，涉及到矩阵的特征值问题。给定矩阵`A`，利用`P=poly(A)`求出矩阵的特征多项式，再通过`r=roots(P)`找到特征值。这有助于理解矩阵的性质和行为。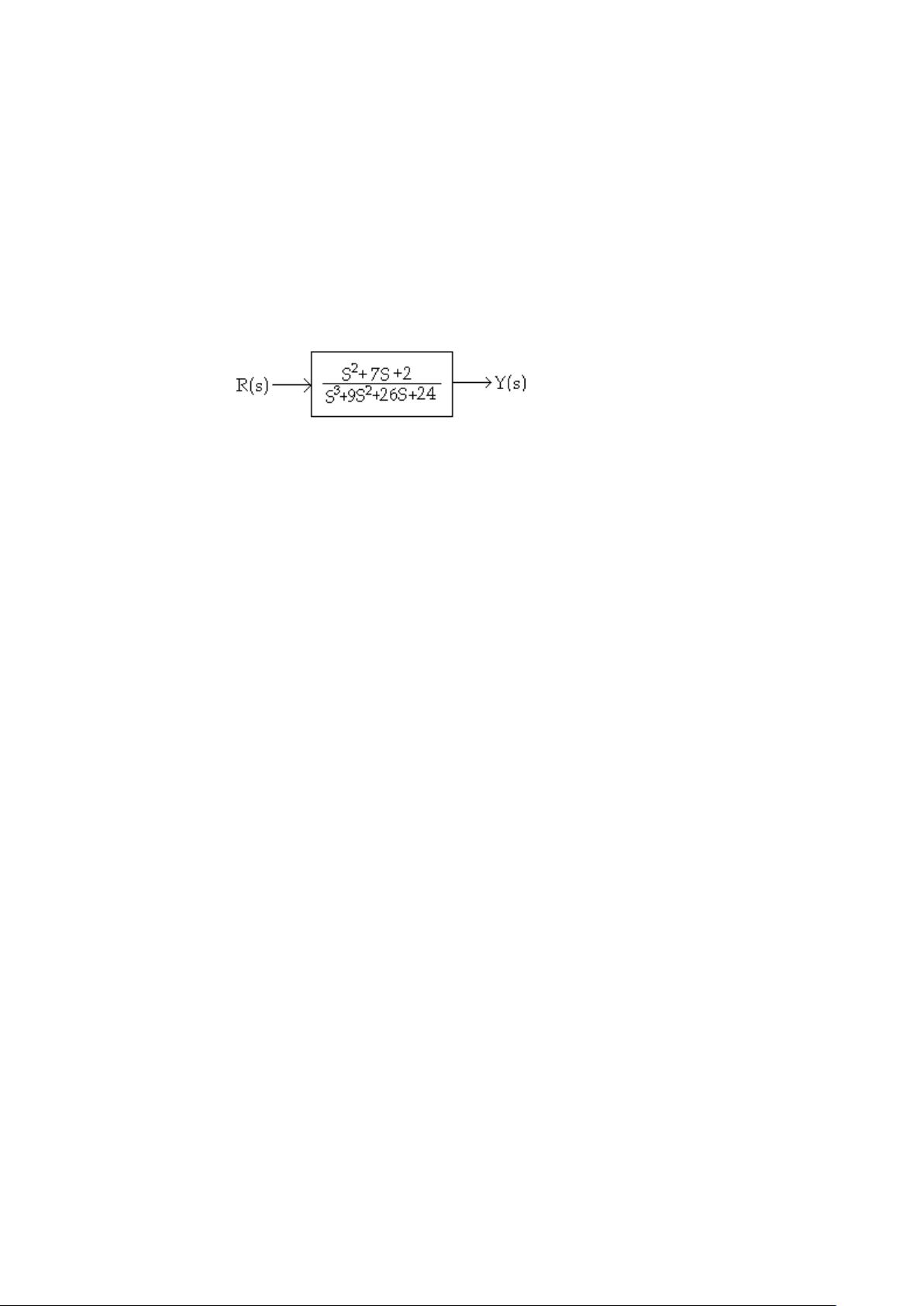 传递函数是控制系统理论中的关键概念，例1.7展示了如何使用`tf2zp`函数获取传递函数的零点（系统响应衰减到零的频率）、极点（系统响应振荡的频率）以及增益。之后，根据这些参数，可以利用`zp2tf`函数构造出传递函数。 最后，例9涉及部分分式展开，这是一种将复数传递函数分解成简单因子形式的技术，对于系统分析和控制设计具有重要意义。这部分内容未在提供的部分给出具体示例，但通常涉及`residue`或`frac`函数来实现。 总结来说，这个文档提供了MATLAB在多项式根计算、矩阵特征值求解和传递函数分析方面的基础操作和技巧，对于理解和应用MATLAB进行信号处理、控制系统设计等工程任务十分有用。