known as PSO-BP algorithm, is proposed for predictio n,
the hybrid algorithm cannot only utilize the global search
capability of PSO, but also strong local search ability of the
BP neural network [20].
For big data sets, the PSO-BP algorithm is not very
accurate and easy to result in a local optimal solution. To
improve the accuracy of customer churn prediction in
telecommunication scenarios, this paper proposes the
PBCCP algorithm.
3 Algorithm design
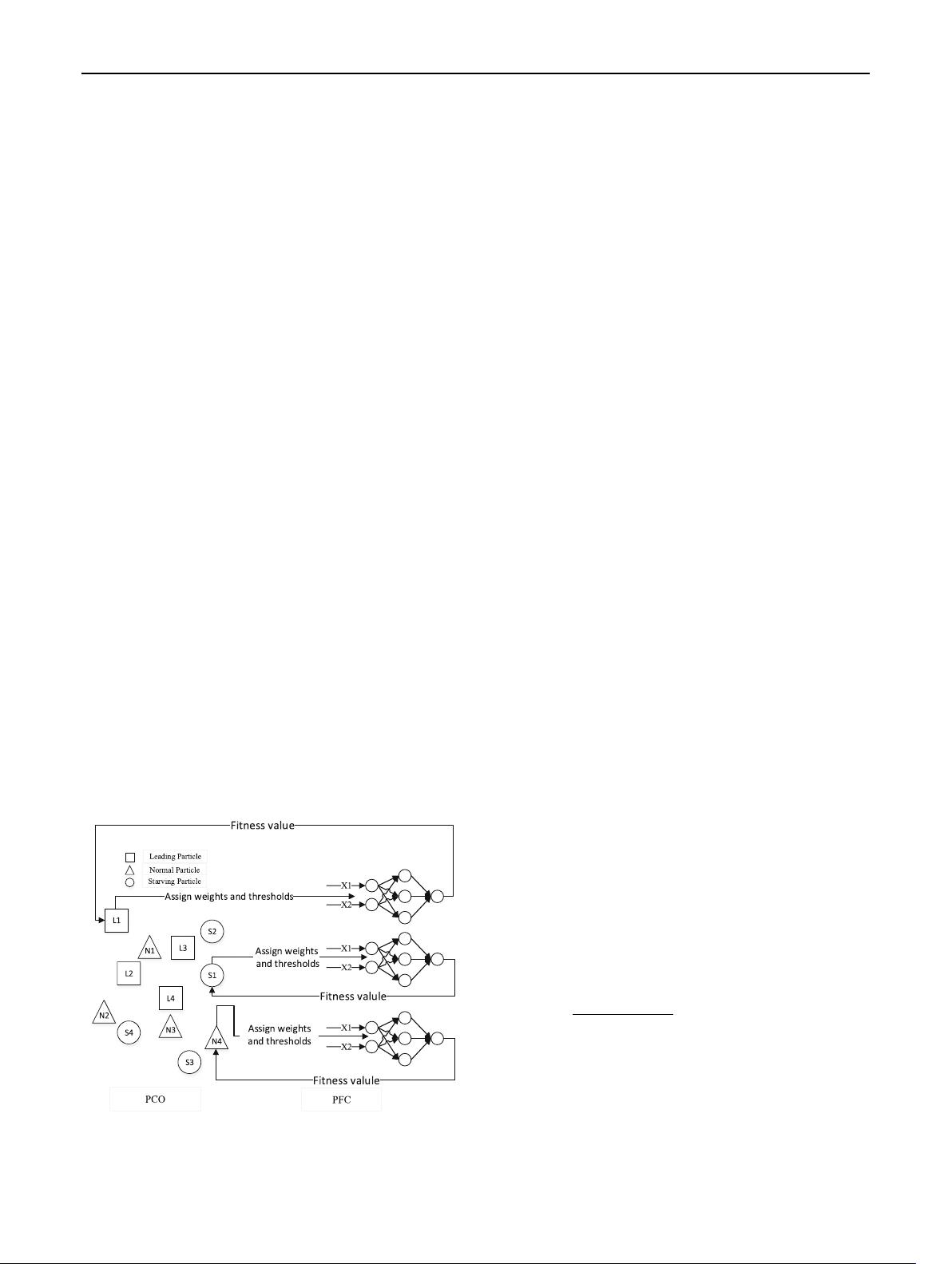
The PBCCP algorithm is an iterative process of the particle
classification optimization (PCO) and the particle fitness
calculation (PFC). The particle here is a vector consisting
of all weights and thresholds of a BP neural network. The
learning error of the neural network is defined as the fitness
value of a partic le. PCO classifies the particles into three
categories according to their fitness values, and updates the
velocity of different category of particles using distinct
equations. PFC calculates the fitness value of a particle in
each forward training process of the BP neural network.
The process of PBCCP is depicted in Fig. 1
The neural network is trained with telecommunication
big data. When PBCCP terminates, the best particle will be
used for initializing the weights and thresholds of the BP
neural network. The neural network is further trained using
the error-backpropagation method, and is expl oited for
customer churn predict ion after the network converges.
3.1 Particle classification opti mization
The particle classification optimization (PCO) method
proposed in this paper classifies particles into three
categories (starving particles, leading particles, and normal
particles).
Assume that the population size is N.InaD-dimen-
sional space, the position of the ith particle can be
expressed as a D-dimensional vector X
i
¼ðx
i1
; x
i2
; ...;
x
iD
Þ
T
:V
i
¼ðv
i1
; v
i2
; ...; v
iD
Þ
T
is the velocity of the i-th
particle. P
i
¼ðp
i1
; p
i2
; ...; p
iD
Þ
T
is the best position which
the i-th particle has found, and P
g
¼ðp
g1;
p
g2
; ...; p
gD
Þ
T
is
the best position which the population has found.
3.1.1 Particle velocity updating
The fitness value of the i-th particle is defined as fitðX
i
Þ,which
is the learning error of the BP neural network (see Sect. 3.2
for the fitness calculation). The particles are classified by their
fitness values. The 1/3 particles with lowest (best) fitness
value are defined as the leading particles, the 1/3 particles
with highest (worst) fitness value are called the starving
particles, and the other particles are the normal particles.
Normal particles somehow impact the movement of
leading particles, and have push effect on the leading
particles. Each leading particle is influenced by the
neighboring normal particles.
The balance betwee n exploration and exploitation in
PCO is decided by the velocity updating process. Thus,
proper velocity updating equation is very important in
finding the global optimum.
In PCO, each category of particles has a specific
velocity updating equation.
Leading particles Leading particles play an important
role in guiding forward direction of the particle swarm.
The leading particles’ velocity updating equation is
V
k
i
¼ xV
k1
i
þ c
1
r
1
ðP
k1
i
X
k1
i
Þþc
2
r
2
ðP
k1
g
X
k1
i
Þ
þ E
h
ðV
k1
i
V
k2
i
Þð1Þ
where variables r
1
and r
2
are two random numbers in the
range [0, 1]. c
1
and c
2
are two positive constants, which are
called the learning factor or accelerating factor. c
1
is used to
adjust the step length of the particle flying to its own best
position, and c
2
is used to adjust the step length of the particle
flying to the swarms best position. The inertia weight x is the
parameter that controls the impact of the previous velocity on
the current one, which is updated as in Eq. 2.
x ¼ x
max
ðx
max
x
min
Þg
G
ð2Þ
g is the generation index representing the serial number of
current evolutionary generation, and G is a predefined
maximum number of generations. E
h
is the sum influence
degree of the normal particles on a leading particle, which
can be calculated through Eq. 3.
Fig. 1 Process of PBCCP
Neural Comput & Applic
123









