计算几何精讲：刘汝佳NOI冬令营课程

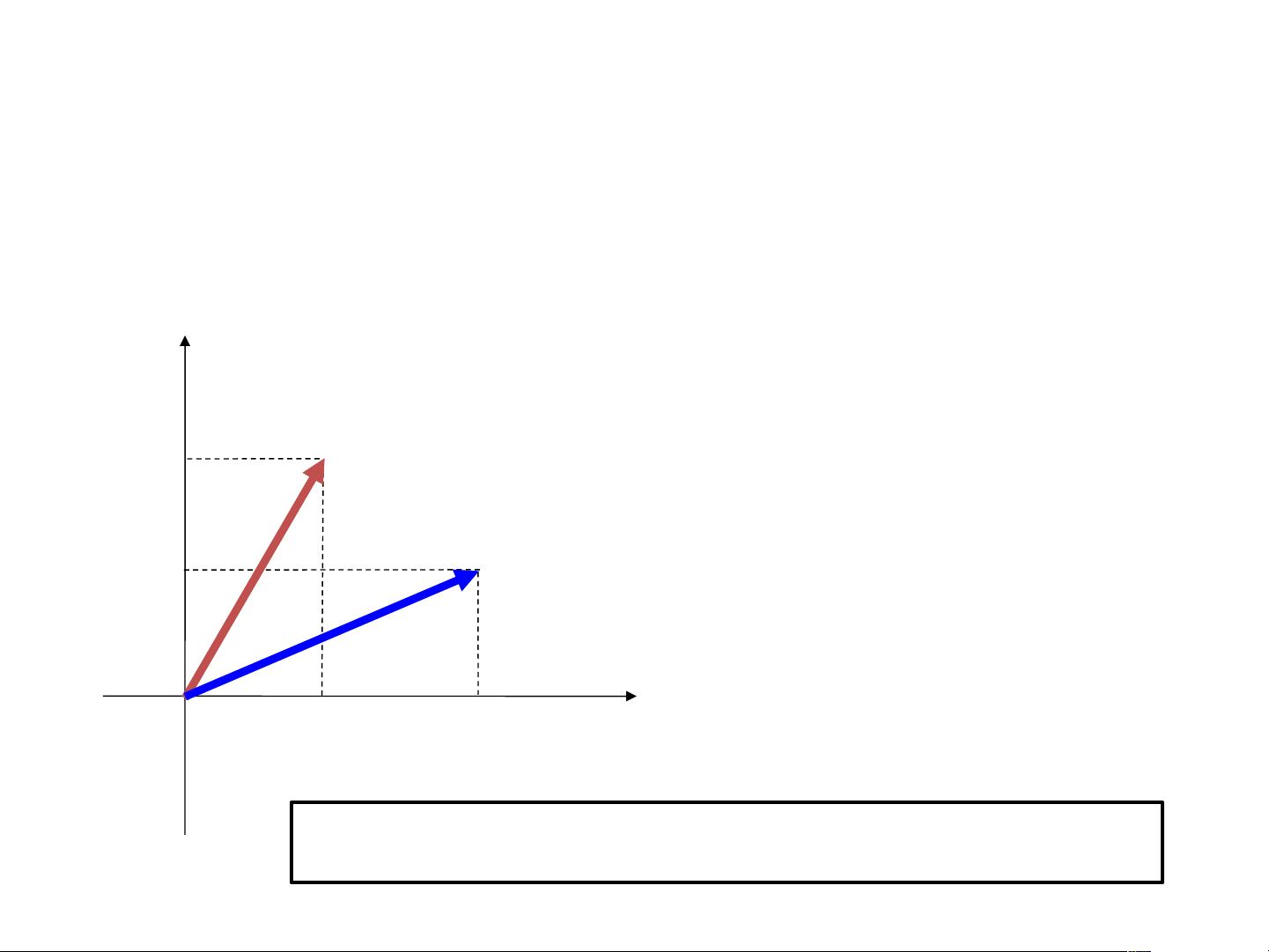
"这是刘汝佳在2011年全国青少年信息学奥林匹克竞赛冬令营的讲稿，主要内容聚焦于计算几何，特别是三维凸包问题。" 在计算几何领域，点和向量是基础概念。点(points)表示空间中的位置，而向量(vectors)具有长度和方向，常用来描述运动或变化。在二维和三维空间中，点和向量的运算有所不同。例如，两个向量相加得到一个新的向量，两个点相减则得到一个向量，这在2D和3D空间中都适用。然而，点与点相加是没有定义的。 坐标系在2D和3D空间中扮演着重要角色，它通过原点(Origin)来定义点和向量的关系。坐标可以用来表示点的位置，也可以用于计算向量的属性。例如，在二维空间中，点P的坐标由(x, y)表示，而在三维空间中，点P的坐标则是(x, y, z)。 点积是向量之间的一种运算，它在2D中定义为v·w = vx * wx + vy * wy，而在3D空间中，这个公式扩展为v·w = vx * wx + vy * wy + vz * wz。点积有多种应用，例如求向量在另一个向量上的投影、判断两个向量是否垂直等。当两个向量的点积为零时，它们垂直。此外，点积还可以用于计算2D中两点间的距离。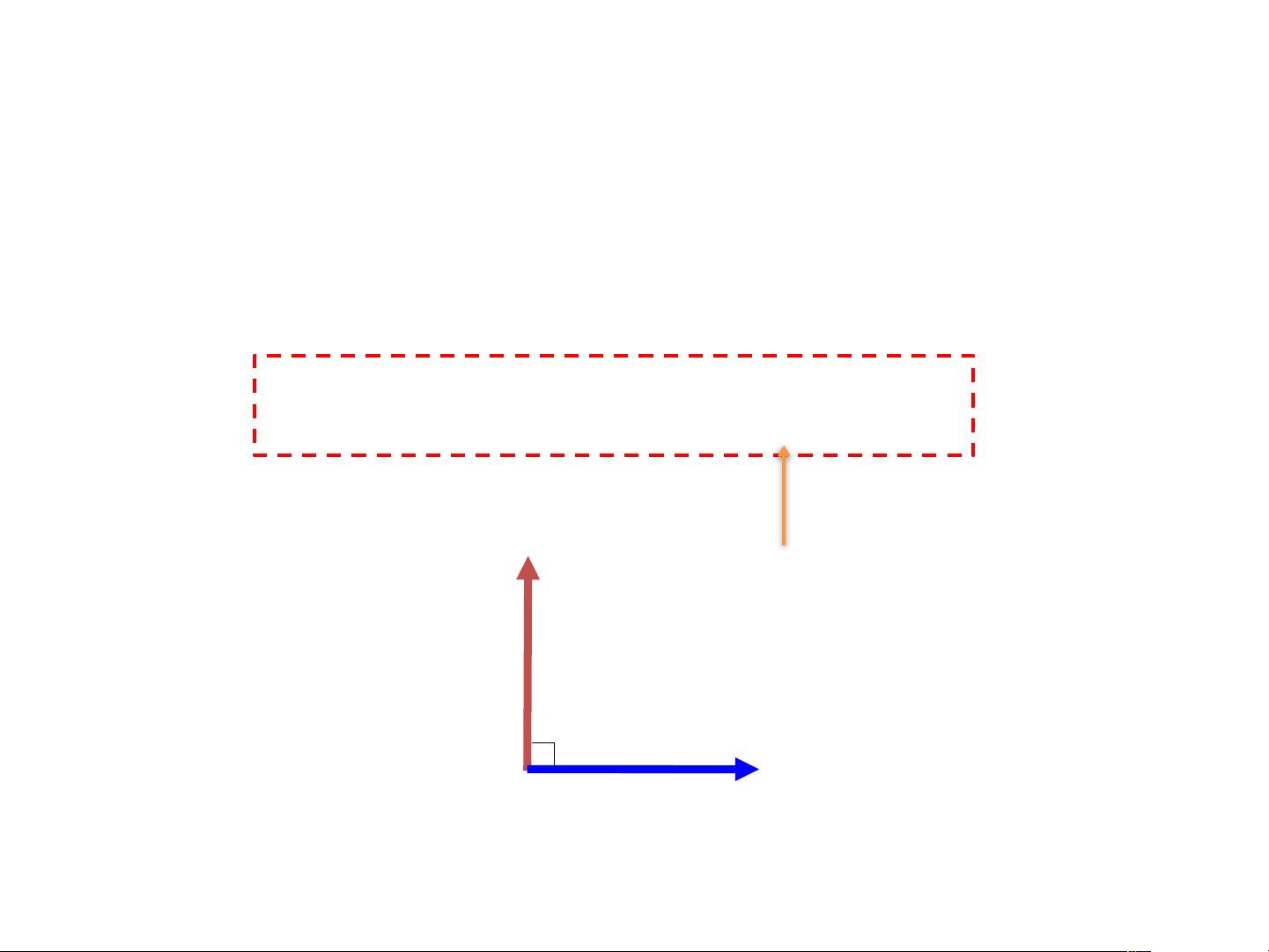 直线和射线的参数方程在2D和3D空间中也十分关键。对于直线，参数方程可以表示为p = p0 + tv，其中p0是直线上的一个已知点，t是参数，v是直线的方向向量。如果限制t的取值范围，可以得到射线的参数方程。在2D中，直线的一般式是Ax + By + C = 0，可以根据这个方程判断两条直线是否相交。同样，3D中的平面可以用点法式表示，即平面π由法向量n和平面上的点p0确定，满足条件<n, p - p0> = 0。 计算点到直线或平面的距离是计算几何中的常见问题。2D中，点到直线的距离可以通过构建垂直于直线的向量并计算其长度来得到。3D中，点到平面的距离可以将点投影到平面的法向量上，然后计算投影点与原点之间的距离。平面的一般式在3D中为Ax + By + Cz + D = 0，可以用来判断点是否在平面内，或者直线和平面是否相交。 刘汝佳的讲稿深入浅出地介绍了这些概念，对理解和解决计算几何问题提供了宝贵的指导。特别是对于三维凸包问题，这部分内容尤为重要，因为三维凸包是许多复杂几何算法的基础，如最近点对查找、碰撞检测等。通过学习这些基础知识，参赛者可以更好地应对信息学竞赛中的几何挑战。