linear program with a constant factor approxima-
tion. There, the input was assumed to be metric,
i.e., nonnegative, symmetric, and satisfying the
triangle inequality . In contrast, affinity propagation
can take as input general nonmetric similarities.
Affinity propagation also provides a conceptually
new approach that works well in practice. Where-
as the linear programming relaxation is hard to
solve and sophisticated software packages need to
be applied (e.g., CPLEX) , affinity propa gation
makes use of intuitive message updates that can
be implemented in a few lines of code (2).
Affinity propagation is related in spirit to tech-
niques recently used to obtain record-breaking
results in quite different disciplines (16). The ap-
proach of recursively propagating messages
(17)ina“loopy graph” has been used to ap-
proach Shannon’s limit in error-correcting de-
coding (18, 19), solve random satisfiability
problems with an order-of-magnitude increase in
size (20), solve instances o f the NP-hard two-
dimensional phase-unwrapping problem (21), and
efficiently estimate depth from pairs of stereo
images (22). Yet, to our knowledge, affinity prop-
agation is the first method to make use of this idea
t o s o l ve the age-old , fundamental problem of
clustering data. Because of its simplicity, general
applicability, and performance, we believ e aff in -
ity propagation will prove to be of broad value in
science and engineering.
References and Notes
1. J. MacQueen, in Proceedings of the Fifth Berkeley
Symposium on Mathematical Statistics and Probability,
L. Le Cam, J. Neyman, Eds. (Univ. of California Press,
Berkeley, CA, 1967), vol. 1, pp. 281–297.
2. Supporti ng material is available on Science Online.
3. Software implementations of affinity propagation, along
with the data sets and similarities used to obtain the
results described in this manuscript, are available at
www.psi.toronto.edu/affinitypropagation.
4. B. J. Frey et al., Nat. Genet. 37 , 991 (2005).
5. K. D. Pruitt, T. Tatusova, D. R. Maglott, Nucleic Acids Res.
31, 34 (2003).
6. C. D. Manning, H. Schutze, Foundations of Statistical
Natural Language Processing (MIT Press, Cambridge, MA,
1999).
7. J. J. Hopfield, Proc. Natl. Acad. Sci. U.S.A. 79, 2554 (1982).
8. M. Charikar, S. Guha, A. Tardos, D. B. Shmoys, J. Comput.
Syst. Sci. 65, 129 (2002).
9. J. S. Yedidia, W. T. Freeman, Y. Weiss, IEEE Trans. Inf.
Theory 51, 2282 (2005).
10. F. R. Kschischang, B. J. Frey, H.-A. Loeliger, IEEE Trans.
Inf. Theory 47, 498 (2001).
11. A. P. Dempster, N. M. Laird, D. B. Rubin, Proc. R. Stat.
Soc. B 39, 1 (1977).
12. S. Dasgupta, L. J. Schulman, Proc. 16th Conf. UAI (Morgan
Kaufman, San Francisco, CA, 2000), pp. 152–159.
13. S. Jain, R. M. Neal, J. Comput. Graph. Stat. 13, 158
(2004).
14. R. R. Sokal, C. D. Michener, Univ. Kans. Sci. Bull. 38 ,
1409 (1958).
15. J. Shi, J. Malik, IEEE Trans. Pattern Anal. Mach. Intell. 22,
888 (2000).
16. M. Mézard, Science 301, 1685 (2003).
17. J. Pearl, Probabilistic Reasoning in Intelligent Systems
(Morgan Kaufman, San Mateo, CA, 1988).
18. D. J. C. MacKay, IEEE Trans. Inf. Theory 45, 399 (1999).
19. C. Berrou, A. Glavieux, IEEE Trans. Commun. 44, 1261
(1996).
20. M. Mézard, G. Parisi, R. Zecchina, Science 297, 812 (2002).
21. B. J. Frey, R. Koetter, N. Petrovic, in Proc. 14th Conf.
NIPS (MIT Press, Cambridge, MA, 2002), pp. 737–743.
22. T. Meltzer, C. Yanover, Y. Weiss, in Proc. 10th Conf. ICCV
(IEEE Computer Society Press, Los Alamitos, CA, 2005),
pp. 428–435.
23. We thank B. Freeman, G. Hinton, R. Koetter, Y. LeCun,
S. Roweis, and Y. Weiss for helpful discussions and
P. Dayan, G. Hinton, D. MacKay, M. Mezard, S. Roweis,
and C. Tomasi for comments on a previous draft of this
manuscript. We acknowledge funding from Natural
Sciences and Engineering Research Council of Canada,
Genome Canada/Ontario Genomics Institute, and the
Canadian Institutes of Health Research. B.J.F. is a Fellow
of the Canadian Institute for Advanced Research.
Supporting Online Material
www.sciencemag.org/cgi/content/full/1136800/DC1
SOM Text
Figs. S1 to S3
References
26 October 2006; accepted 26 December 2006
Published online 11 January 2007;
10.1126/science.1136800
Include this information when citing this paper.
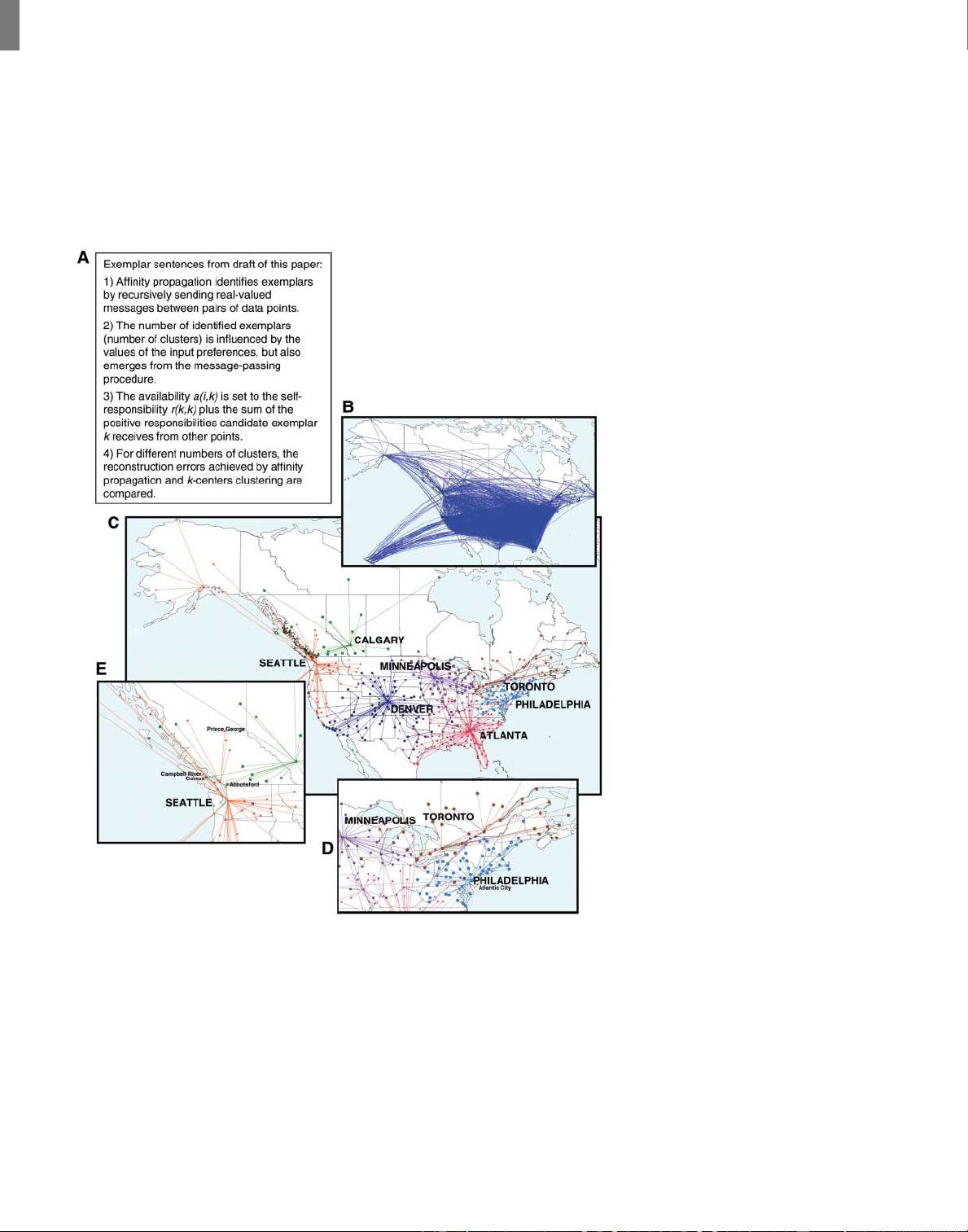
Fig. 4. Identifying key sentences and air-travel routing. Affinity propagation can be used to explore
the identification of exemplars on the basis of nonstandard optimization criteria. (A) Similarities between
pairs of sentences in a draft of this manuscript were constructed by matching words. Four exemplar
sentences were identified by affinity propagation and are shown. (B) Affinity propagation was applied to
similarities derived from air-travel efficiency (measured by estimated travel time) between the 456 busiest
commercial airports in Canada and the United States—the travel times for both direct flights (shown in
blue) and indirect flights (not shown), including the mean transfer time of up to a maximum of one
stopover, were used as negative similarities (3). (C) Seven exemplars identified by affinity propagation are
color-coded, and the assignments of other cities to these exemplars is shown. Cities located quite near to
exemplar cities may be members of other more distant exemplars due to the lack of direct flights between
them (e.g., Atlantic City is 100 km from Philadelphia, but is closer in flight time to Atlanta). (D)Theinset
shows that the Canada-USA border roughly divides the Toronto and Philadelphia clusters, due to a larger
availability of domestic flights compared to international flights. However, this is not the case on the west
coast as shown in (E), because extraordinarily frequent airline service between Vancouver and Seattle
connects Canadian cities in the northwest to Seattle.
16 FEBRUARY 2007 VOL 315 SCIENCE www.sciencemag.org
976
REPORTS
on February 15, 2007 www.sciencemag.orgDownloaded from









