图数据结构详解：无向图、有向图与完全图的概念

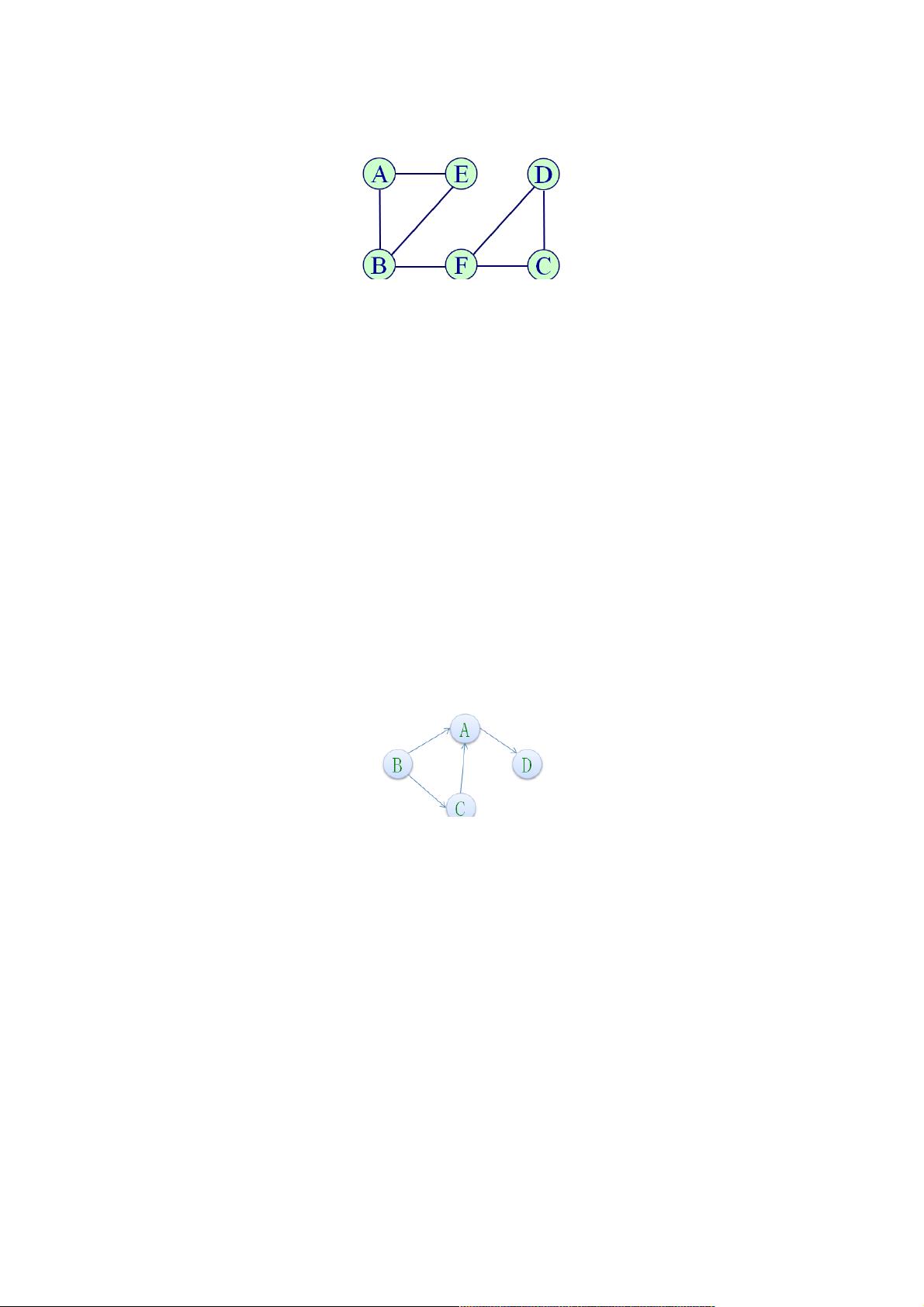
本文将详细探讨数据结构与算法中的图概念，主要关注图的基本定义、存储结构以及与线性表和树的区别。我们将讨论无向图、有向图、简单图、完全图、稀疏图和稠密图，以及图中的边与顶点之间的关系，如邻接点和度的概念。 在数据结构中，图（Graph）是一种非线性的数据结构，由顶点的有穷非空集合V和顶点之间边的集合E组成，通常表示为G(V,E)。这里的G代表一个图，V是图中顶点的集合，E是边的集合。图的概念不同于线性表和树，线性表中的数据元素被称为元素，树中的数据元素称为结点，而在图中，这些元素被称为顶点。 值得注意的是，线性表可以为空，树可以是空树，但图的顶点集合V在大部分教材中规定必须是有穷非空的。线性表中的元素间存在线性关系，而树结构中结点间有层次关系。在图结构中，任意两个顶点间可能存在关系，这些关系通过边来表示，边集可以为空。边分为无向边和有向边： - 无向边：两个顶点Vi和Vj之间的无向边没有方向，用无序对(Vi,Vj)表示。例如，无向图G1=(V1,E1)包含顶点集合V1={A,B,C,D,E,F}和边集合E1={(A,B),(A,E),(B,E),(B,F),(C,D),(C,F),(D,F)}。 - 有向边（弧）：从顶点Vi到Vj的有向边用有序对<Vi,Vj>表示，Vi称为弧尾，Vj称为弧头。有向图G2={V2,E2}，其中V2={A,B,C,D}，E2={<B,A>,<B,C>,<C,A>,<A,D>}。 简单图是指不存在自环（顶点到自身的边）且不重复出现边的图。无向完全图是任何两个顶点间都有边的无向图，n个顶点的无向完全图有n*(n-1)/2条边。有向完全图则是每个顶点对之间都有方向相反的两条弧，n个顶点的有向完全图有n*(n-1)条边。 图的边或弧数量相对于顶点数量较少的图称为稀疏图，反之为稠密图。当边或弧的数量小于n*logn（n为顶点数量）时，通常认为它是稀疏图。 在图中，如果边(V1,V2)属于边集合E，那么顶点V1和V2互为邻接点，即它们相邻接。边(V1,V2)与顶点V1和V2相关联，说它们依附于这些顶点。顶点V的度（Degree）是指与其相连的边的数量。对于无向图，顶点V的度等于与之关联的无向边数；对于有向图，分为入度（In-Degree，指向顶点的边数）和出度（Out-Degree，从顶点出发的边数）。 在实际应用中，图常用于表示网络、关系、路径等复杂结构，如社交网络中的用户关系、计算机网络中的路由器连接、旅行路线等。带权的图，也就是网络，常常需要进行最短路径、最小生成树等算法处理，这些是图论中的重要问题。 在C语言中，表示图通常采用邻接矩阵或邻接表的方式。邻接矩阵是一个二维数组，其中的元素表示对应顶点之间是否存在边；邻接表则是以链表形式存储与每个顶点相邻接的其他顶点列表，节省空间，适合表示稀疏图。理解并熟练掌握图的概念及其存储结构，对于设计和实现高效算法至关重要。