树链剖分算法详解及实现

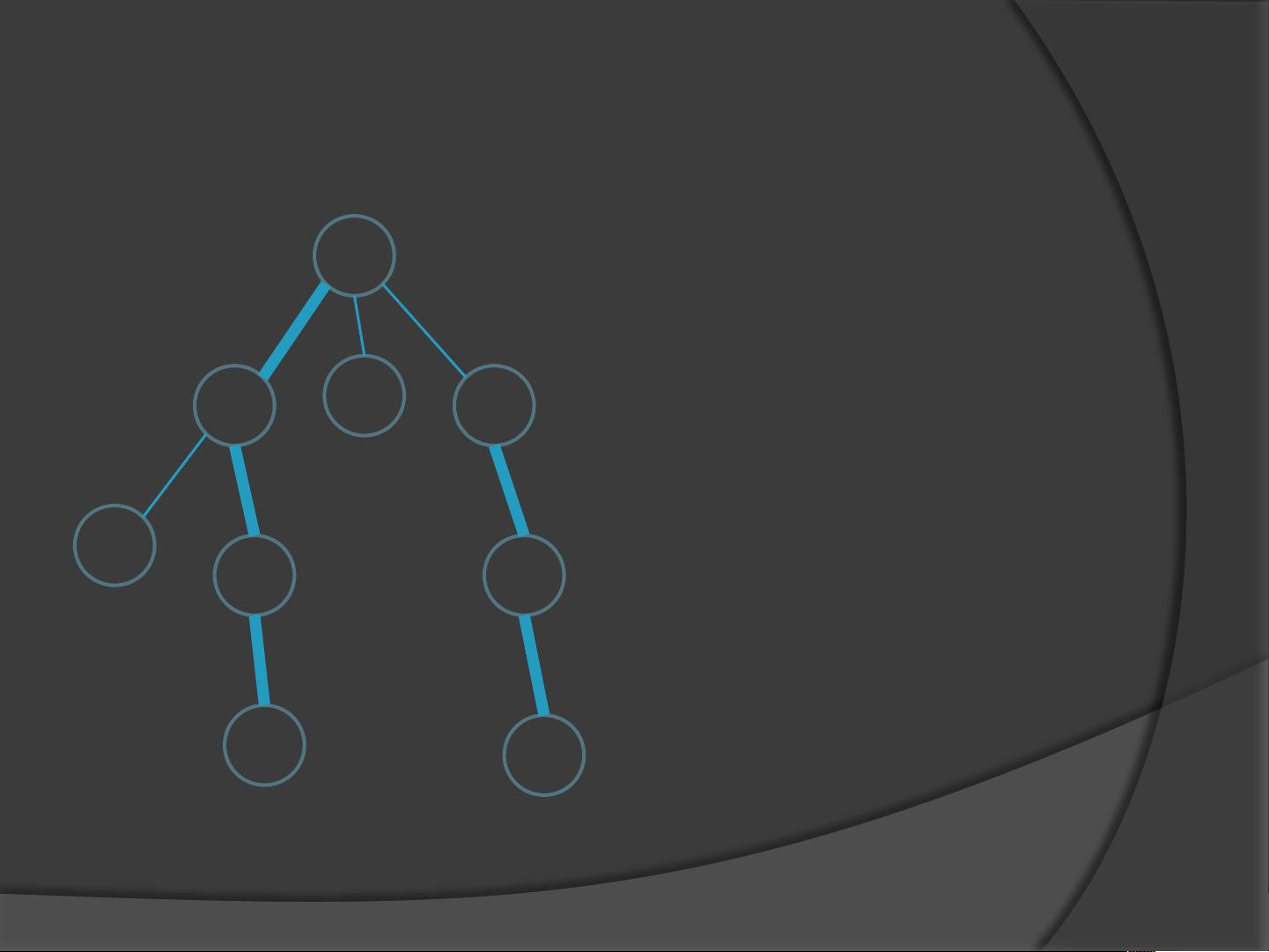
"树链剖分算法.pptx 涵盖了树链剖分的基本概念、实现方式以及其在解决树形结构问题中的应用。江苏省大丰高级中学的蒋一瑶介绍了如何通过轻重边剖分将树划分为多条链，并利用数据结构如树状数组、BST、SPLAY或线段树来高效维护这些链，以达到路径信息的快速维护，复杂度为O(logN)。" 树链剖分是一种针对树的数据结构优化技术，主要目的是为了更有效地处理树上的路径信息。通过将树分为多条链，每条链上的节点数量相对较少，从而可以使用高效的数据结构来维护链上的信息，例如查询与更新操作。 在树链剖分中，关键的概念包括轻边和重边。轻边是指树中那些连接两个大小接近的子树的边，而重边则是连接一个大子树和一个小子树的边，具体来说，如果节点V是节点U的儿子，且size[V]小于等于size[U]的一半，则边(U, V)被视为轻边。相反，如果size[V]大于size[U]的一半，边(U, V)则为重边。重路径（重链）是由重边组成的路径，这样的路径在树中非常稀少，从根节点到任意节点最多只有O(logN)条重路径。 实现树链剖分通常需要两次深度优先搜索（DFS）。第一次DFS用于找到树中的重边，第二次DFS则将重边连接起来形成重链。在找重边的过程中，每个节点会记录其子节点中size值最大的那个节点，即重边的另一端。然后，通过CONNECT-HEAVY_EDGE函数，自根节点开始，沿着重边向下扩展，构建出重链。对于不在当前重链上的节点，会以该节点为起点重新拉出一条新的重链。 维护树链剖分后，每条重链都可以看作是一个区间，可以使用如树状数组、BST（二叉搜索树）、SPLAY（自旋树）或线段树等数据结构来高效地处理链上的节点。这样，在需要处理路径信息时，复杂度可以降低到O(logN)，显著提高了算法的效率。 树链剖分的应用广泛，常见于树的查询和修改问题，如路径上的节点统计、最短路径计算、路径上的点更新等。通过树链剖分，可以将原本需要线性时间复杂度的问题优化到对数时间复杂度，对于大规模数据的处理具有重要意义。