C++实现大数快速模幂运算
79 浏览量
更新于2024-09-02
收藏 59KB PDF 举报
"C++使用string实现大数快速模幂运算"
在C++编程中,处理大数是一项挑战,因为标准库中的数据类型如`int`, `long long int`等都有其数值范围限制。当需要处理超过这些范围的数时,就需要自定义数据结构或使用特殊库来存储和操作大数。本教程主要介绍如何使用C++的`string`类型来实现大数的快速模幂运算。
首先,大数通常是指超出常规整型数据类型的数值,它们可能包含数百甚至数千个位。由于C++的标准库并不直接支持大数运算,因此我们需要利用字符串来模拟大数的存储和运算过程。字符串可以容纳任意长度的字符序列,非常适合用来表示大数。
在大数的运算中,模幂运算(即求一个数的幂并对模运算后的结果取模)是一项基础且重要的操作。快速模幂算法是一种高效的计算方法,它的核心思想是利用幂运算的二进制展开式,将指数转换为二进制形式,然后通过平方和乘法的组合实现指数的快速计算。
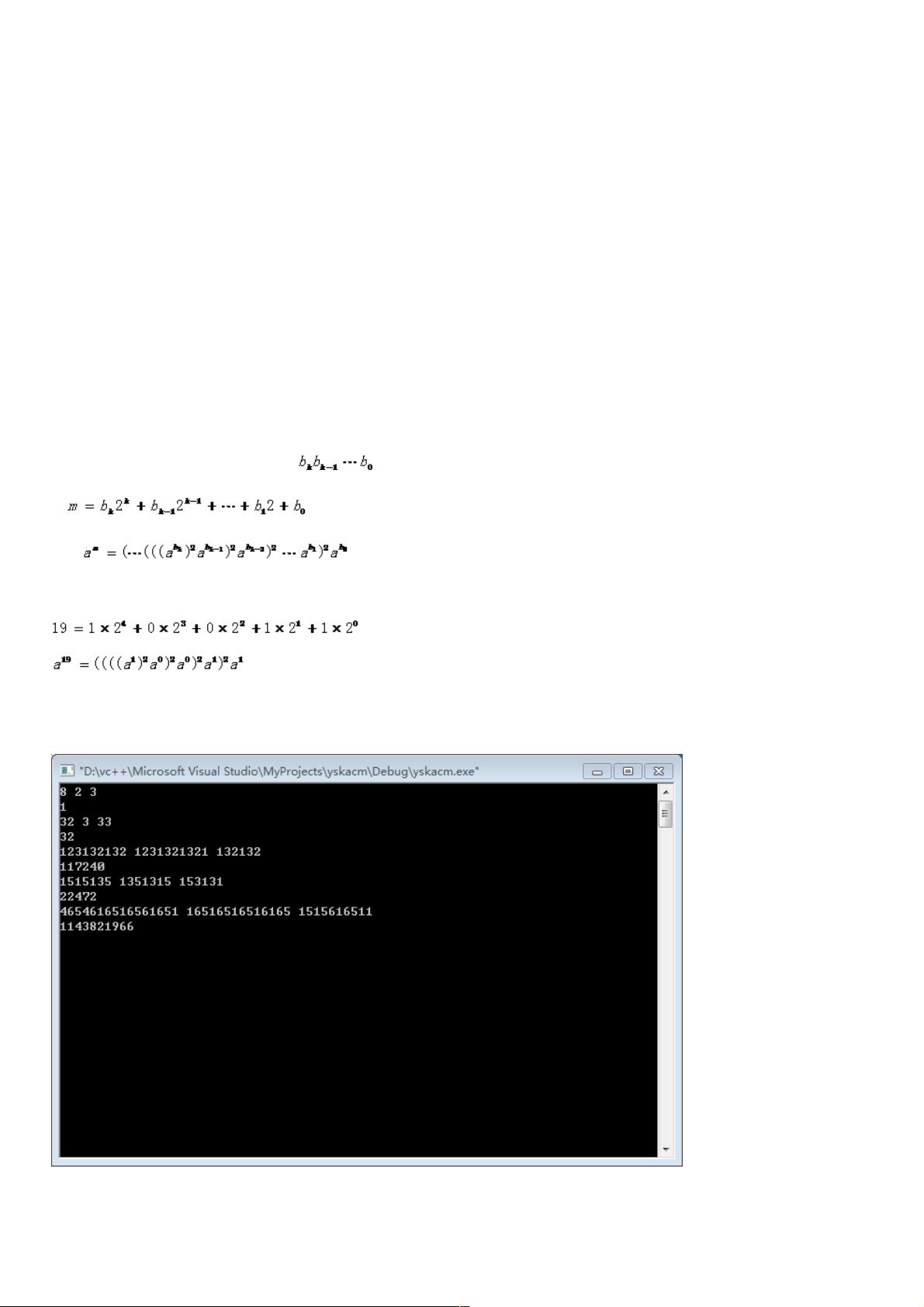
例如,如果要计算`a^m mod p`,其中`a`、`m`是正整数,`p`是模数,将`m`表示为二进制形式`m = m_n * 2^n + m_{n-1} * 2^{n-1} + ... + m_1 * 2^1 + m_0 * 2^0`,则可以逐步计算:
1. 计算`a^(2^n) mod p`
2. 根据`m`的二进制位,每次对结果平方并取模,直到所有二进制位处理完
这种算法的时间复杂度为O(log m),大大减少了计算量,尤其在处理大数时非常有效。
在给出的代码中,可以看到辅助函数`dezero`用于去除字符串前导的零,`judge`用于比较两个大数的大小,`minus`用于执行大数减法。这些都是实现大数运算的基础工具。快速模幂算法的核心部分通常包括一个循环,每次迭代根据当前二进制位决定是否进行乘法和取模操作。
此外,还需要注意在处理字符串表示的大数时,由于`char`类型在C++中是符号整型,其值范围有限,可能会导致正数的误表示。例如,`char a = 161; cout << (int)a;`会输出-95,因为`char`的首位比特用于表示正负,而161在二进制中表示为`10100001`,首位为1表示负数,因此转换为`int`时解释为负值。为了避免这类问题,应该使用字符串存储大数,并使用字符串的API进行操作。
C++使用`string`进行大数快速模幂运算需要对字符串操作、二进制运算以及高效算法有深入理解。在实际编程中,可以结合`algorithm`库中的函数,如`reverse`, `find`, `transform`等,以及自定义的辅助函数,来实现复杂的大数运算。
2011-07-15 上传
点击了解资源详情
2020-09-03 上传
2015-04-18 上传
2021-10-31 上传
2007-05-12 上传
2019-05-05 上传
2019-07-24 上传
2015-01-06 上传
weixin_38618094
- 粉丝: 4
- 资源: 912
最新资源
- WeatherApp
- Marlin-Anet-A8:我的自定义设置的Marlin Anet A8配置
- Fit-Friends-API:这是使用Python和Django创建的Fit-Friends API的存储库。该API允许用户创建用户和CRUD锻炼资源。 Fit-Friends是一个简单但有趣的运动健身分享应用程序,通过对保持健康的共同热情将人们聚集在一起!
- CakePHP-Draft-Plugin:CakePHP插件可自动保存任何模型的草稿,从而允许对通过身份验证超时或断电而持久保存的进度进行数据恢复
- A星搜索算法:一种加权启发式的星搜索算法-matlab开发
- spmia2:Spring Cloud 2020的Spring Cloud实际应用示例代码
- LichVN-crx插件
- Mastering-Golang
- DhillonPhish:我的GitHub个人资料的配置文件
- 园林绿化景观施工组织设计-某道路绿化铺装工程施工组织设计方案
- 自相关:此代码给出离散序列的自相关-matlab开发
- Guia1_DSM05L:Desarrollo de la guia 1 DSM 05L
- FPS_教程
- Campanella-rapidfork:Campanella的话题后端
- os_rust:我自己的用Rust编写的操作系统
- Allociné Chrome Filter-crx插件