完全二叉树与堆的概念及操作——C++实现

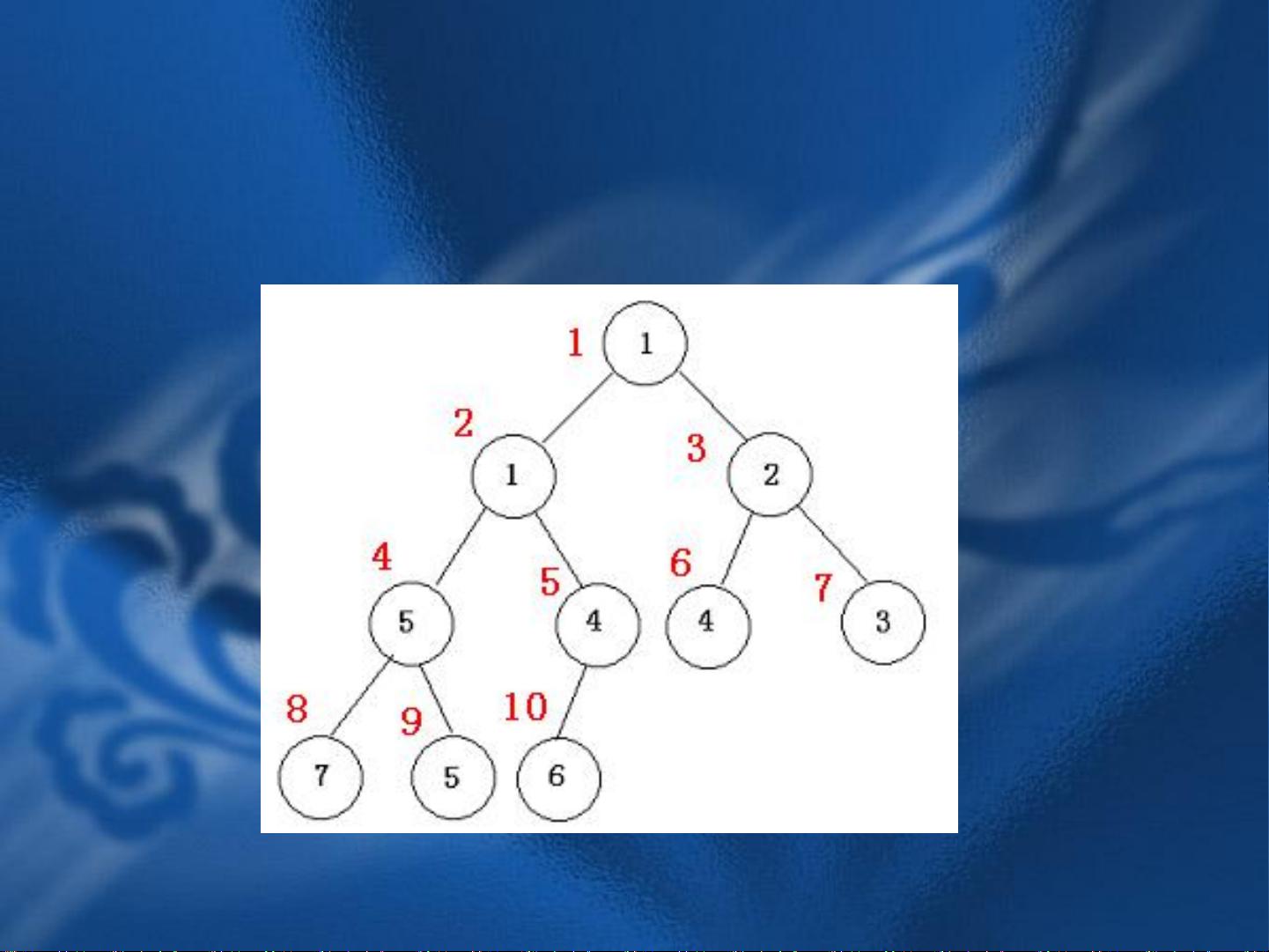
"这篇文档详细介绍了堆及其应用，主要针对C++编程环境。内容包括完全二叉树的概念，堆的定义，堆的性质，以及堆的主要操作，如put（添加元素）和get（删除元素）操作。" 在计算机科学中，堆是一种特殊的树形数据结构，通常用于实现优先队列。在本章节中，首先提到了完全二叉树的概念，这是理解堆的基础。完全二叉树是一类高度平衡的二叉树，其中除了最后一层外，其他各层的节点数都是满的，且最后一层的节点都尽可能地靠左排列。 接下来，堆被定义为一种基于完全二叉树的数组实现的数据结构。每个节点在数组中的位置与其在树中的位置相对应，根节点位于数组的第一个位置，即A[1]，子节点可以通过简单的数学计算得到，例如左孩子结点的下标是2i，右孩子结点是2i+1，而父节点的下标则是i/2。 堆的两个关键性质是大根堆和小根堆。在大根堆中，每个节点的值都小于或等于其父节点的值，因此根节点总是存储最大值；相反，小根堆中每个节点的值都大于或等于其父节点的值，根节点存储最小值。这两种性质使得堆成为查找最大或最小元素的理想工具。 堆的主要操作包括put和get。put操作涉及将新元素添加到堆中，这个过程通常需要自底向上地调整堆，确保新的元素在适当的位置以满足堆的性质。get操作则涉及删除并返回堆顶（通常是最大或最小值）的元素，之后需要自顶向下地调整堆以保持其结构。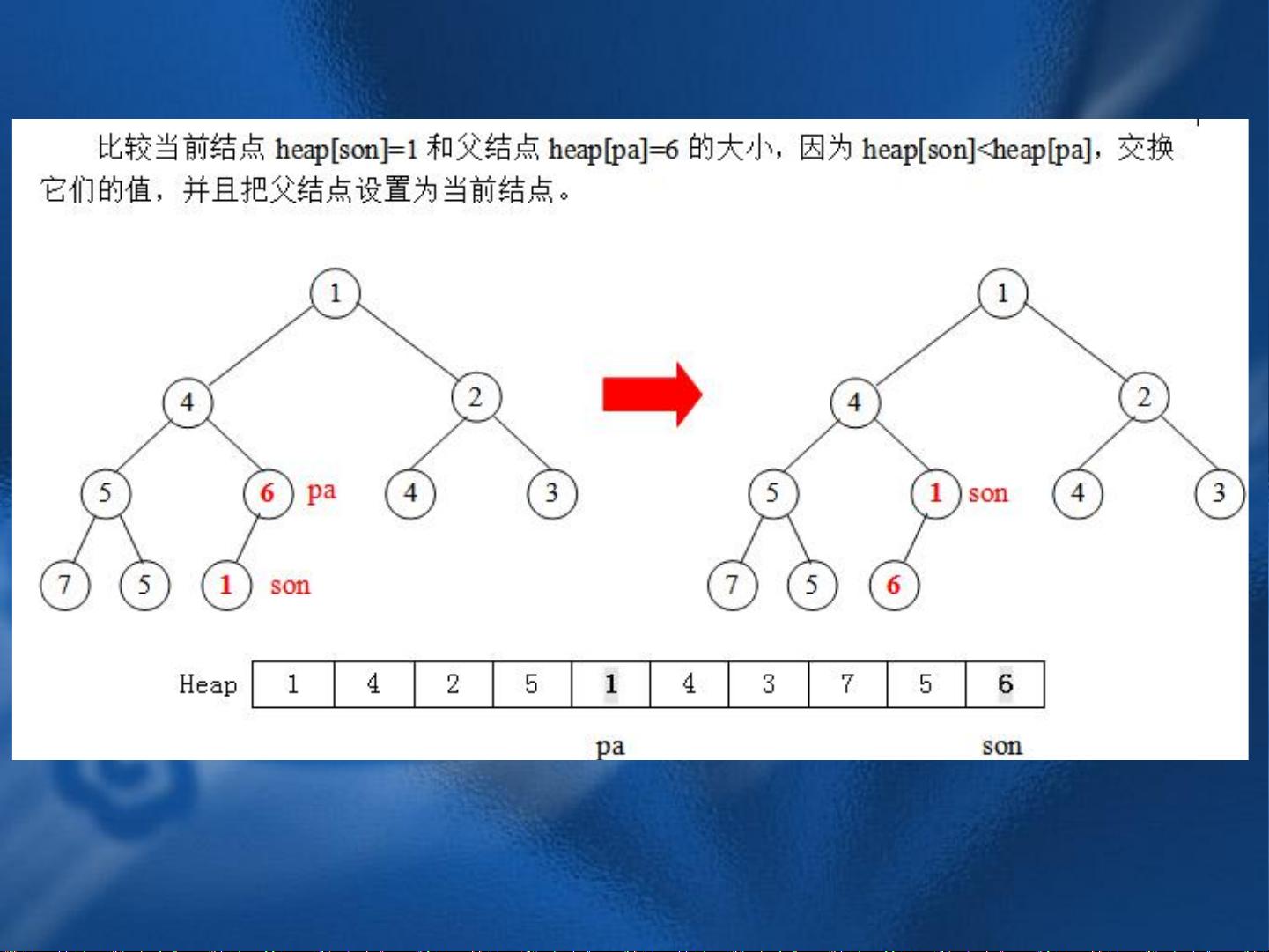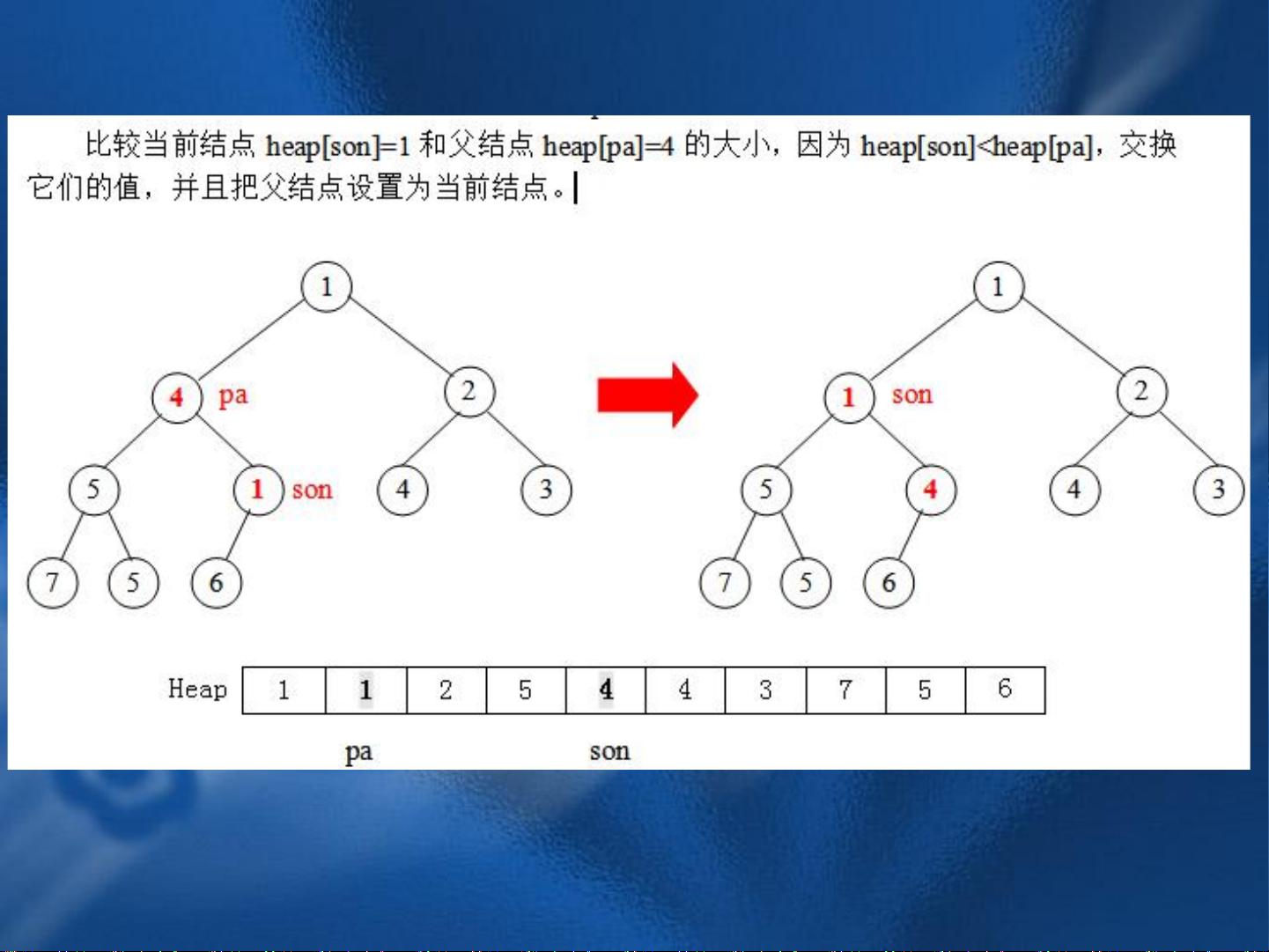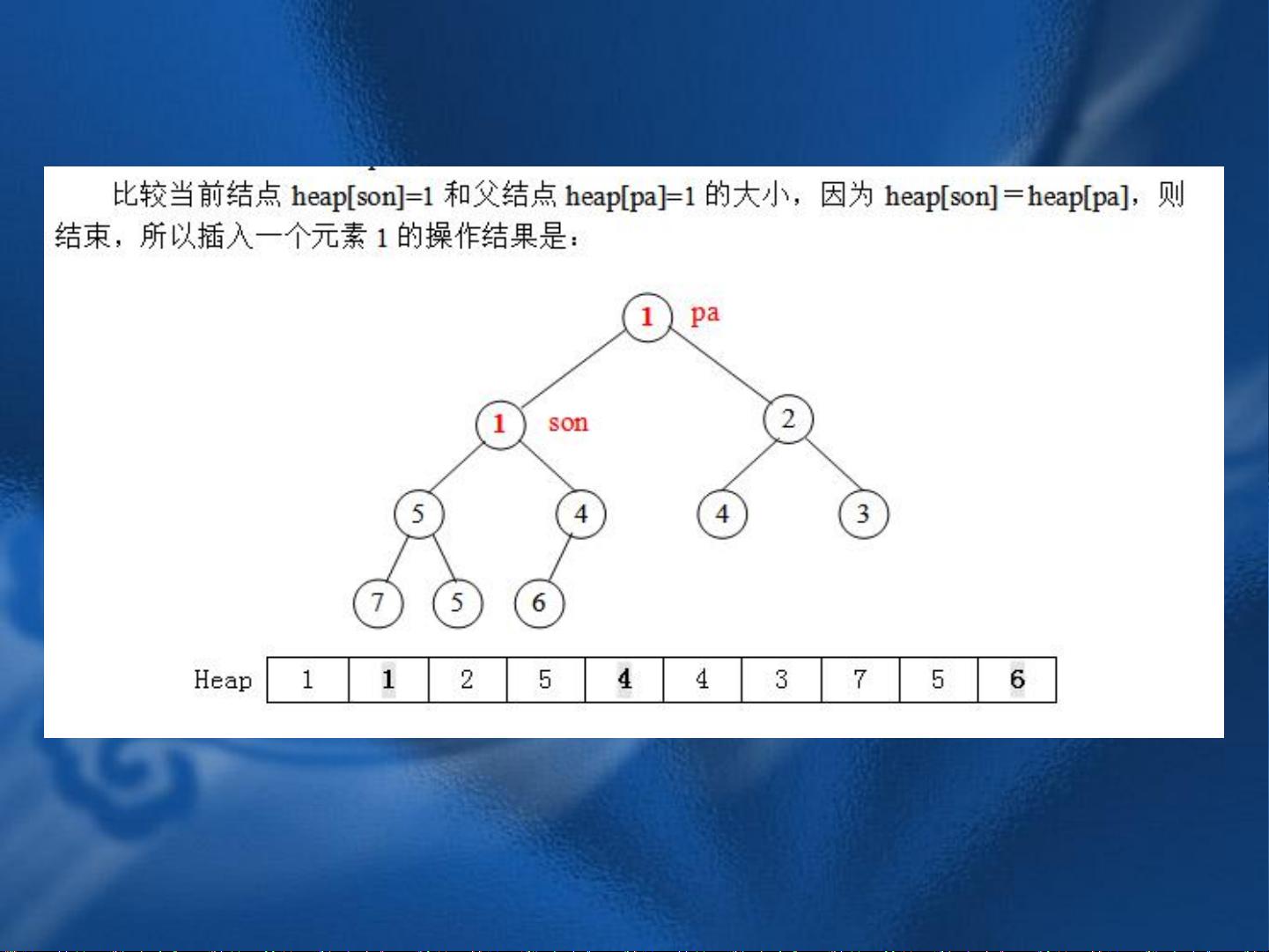 例如，通过put操作建立小根堆的过程是，每次插入一个元素后，将其与父节点进行比较，如果元素小于父节点，就交换它们的位置，然后继续向上比较，直到满足堆的性质或者到达根节点。反复进行put操作，可以逐步构建出一个小根堆。 在实际应用中，堆常用于优先队列、事件调度、数据排序（如希拉里-克努斯排序）等场景。在C++中，标准库提供`<queue>`和`<priority_queue>`等容器，它们可以方便地实现堆操作。理解堆的原理和操作对于编写高效算法至关重要，特别是在处理大量数据时。