响应曲面法在化学工程中的应用与优化

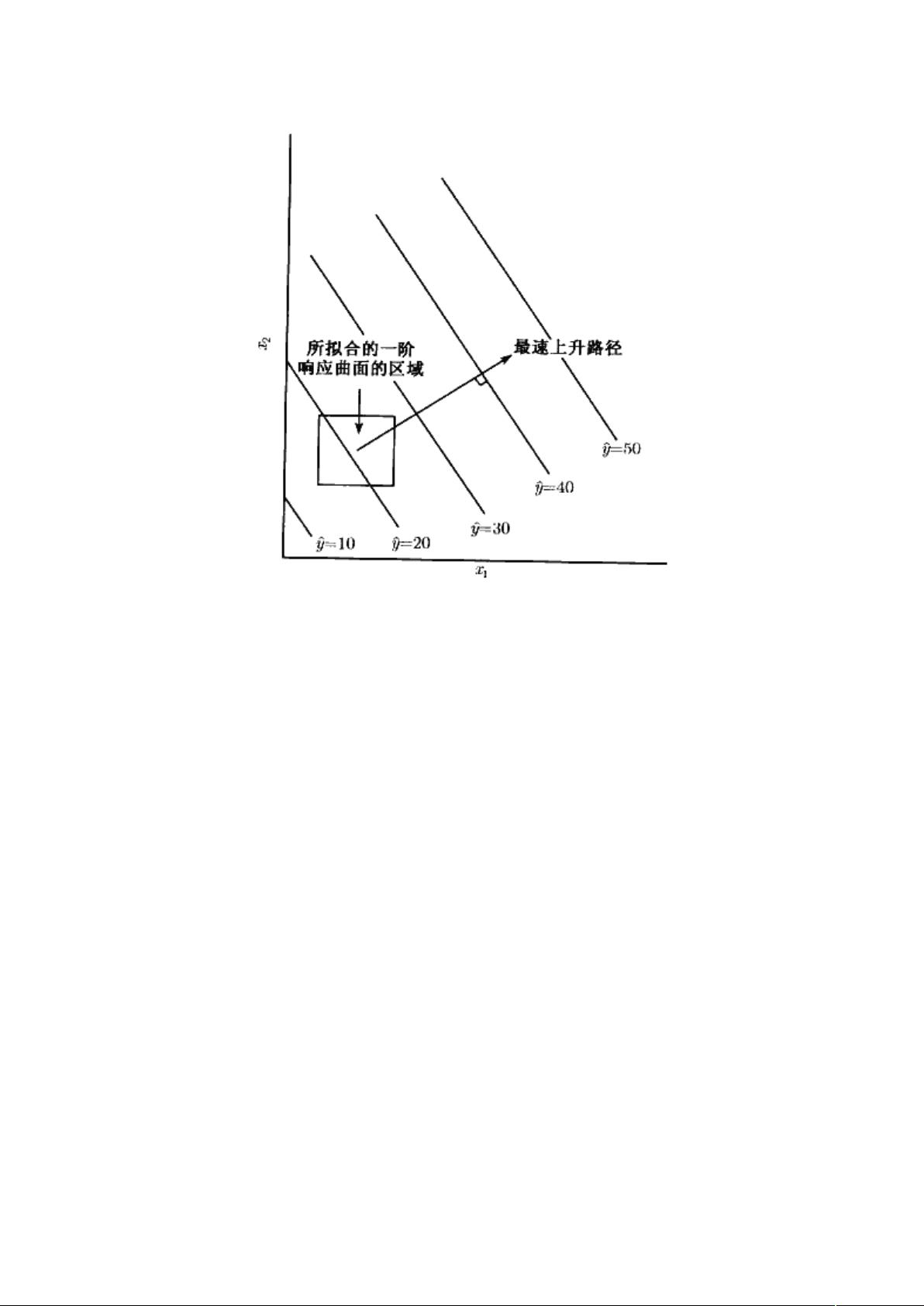
"实验设计与分析相关作业，探讨了响应曲面法在多变量影响响应问题中的应用，以及如何通过低次和高次多项式建模优化响应。" 响应曲面法是一种综合数学和统计学的技术，主要用于研究和优化多个输入变量对单一响应变量的影响。在实际工程和科学问题中，例如化学工程中，可能需要寻找最优的温度(x1)和压强(x2)组合以最大化过程的出品率(y)。这个出品率是这两个变量的函数，而响应曲面则用于可视化这种关系。 响应曲面通常用三维图形表示，其中η表示预期响应，ε表示观测响应的误差或随机因素。图16-1展示了一个响应曲面的例子，图16-2则通过等高线进一步简化了曲面的视觉理解，每个等高线对应一个特定响应值，帮助分析者理解x1和x2变化如何影响响应。 在响应曲面法中，首先需要建立一个能够近似真实响应与独立变量之间关系的函数模型。如果响应与变量的关系近似线性，那么可以使用一阶模型(16-1)。然而，如果存在非线性关系，如系统弯曲，就需要更高次的多项式，如二阶模型(16-2)来拟合数据。 拟合曲面的过程可以通过最小二乘法来实现，目的是估计最接近真实响应的模型参数。响应曲面设计是实验设计的一个分支，旨在有效地收集数据以优化模型的拟合。这种设计策略在第16-4章节中会进一步讨论。 响应曲面法通常是一个迭代过程，开始时可能选择的运行条件远离最优解，随着实验的进行和数据分析，逐步逼近最优操作条件。这种方法特别适用于那些需要在多变量环境中寻找最佳操作点的问题，确保在有限的资源和时间内获得最佳结果。 实验设计与分析是科学研究和工程实践中不可或缺的一部分，通过响应曲面法，我们可以系统地探索复杂系统中的变量交互，并找到最优的操作策略。这不仅有助于提高生产效率，降低成本，还能推动理论理解的深化。