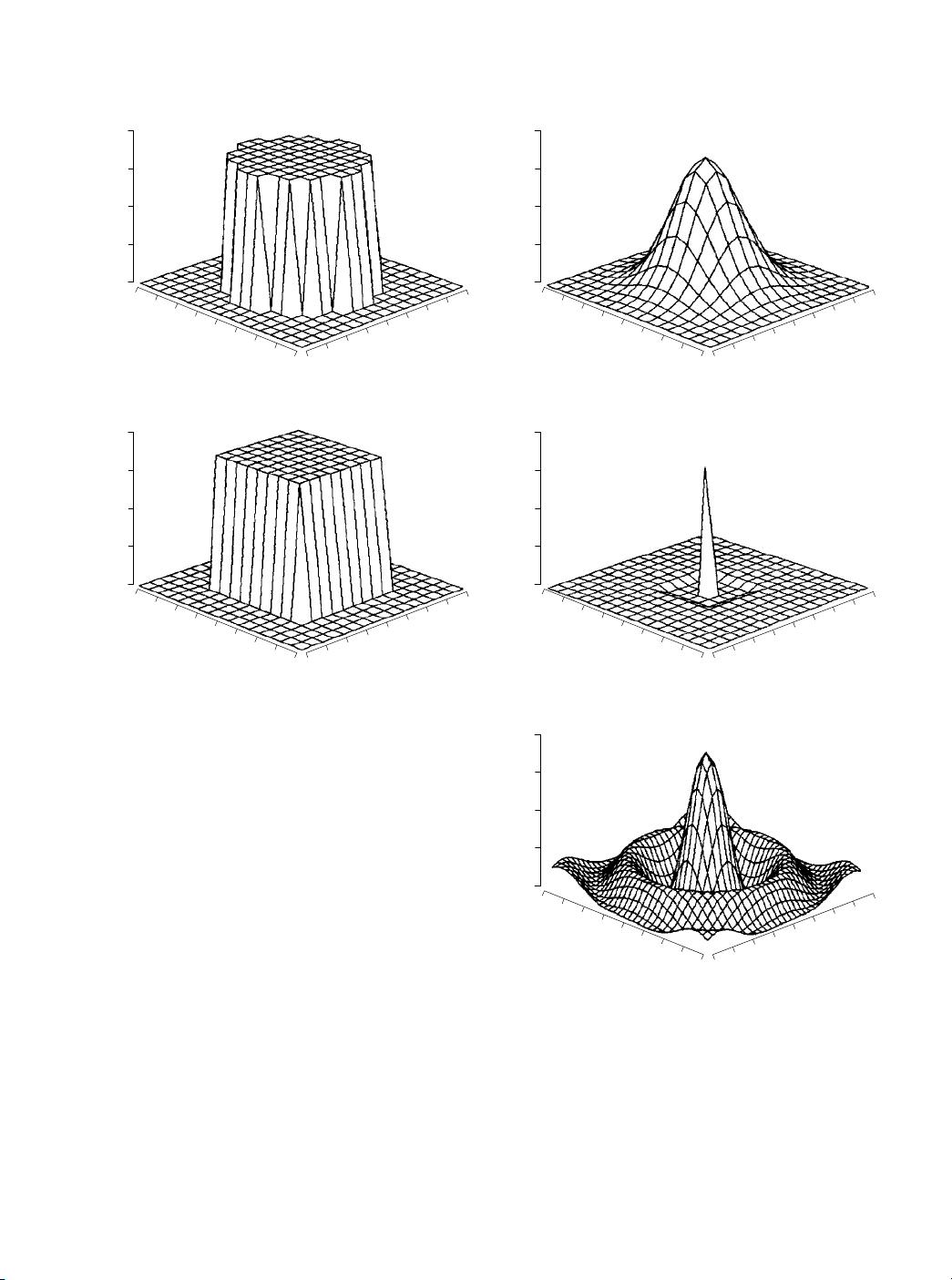
线性图像处理：滤波与傅立叶分析

"The Scientist and Engineer's Guide to Digital Signal Processing - 24 Linear Image Processing" 线性图像处理是数字信号处理（DSP）在图像领域中的应用，主要涉及两种核心技术：卷积和傅立叶分析。其中，卷积是更加关键的技术，因为图像的信息通常在空间域中编码，而非频率域。通过线性滤波，我们可以实现许多图像改进的效果，例如增强物体边缘、降低随机噪声、校正不均匀光照、去模糊和运动校正等。 卷积过程是通过对原始图像与特定滤波核进行卷积操作来实现的，由此产生滤波后的图像。然而，图像卷积的一大挑战在于计算量巨大，可能导致执行时间过长，这在实时或高效处理需求中可能是不可接受的。本章针对各种图像处理任务提供了设计滤波核的策略。 为了减少执行时间，文章中介绍了两种重要的技术： 1. 卷积的可分离性：如果一个二维滤波核可以分解为两个一维滤波核的乘积，那么可以通过分别在一维上进行卷积来显著减少计算量。这种方法特别适用于对称或者近似对称的滤波核。 2. 快速傅立叶变换（FFT）卷积：利用FFT算法可以将卷积转换为在频域中的简单乘法，大大减少了计算复杂度。首先对图像和滤波核进行离散傅立叶变换，然后进行元素间的乘法，最后再进行反傅立叶变换以得到卷积结果。这种方法在处理大型图像时尤其有效。 傅立叶分析在图像处理中的作用主要体现在频域分析。它可以帮助我们理解图像的频率成分，识别图像中的高频（如边缘）和低频（如平坦区域）信息。通过修改频域中的滤波器，可以有针对性地增强或减弱特定频率成分，从而实现不同的图像处理效果。 在实际应用中，例如图像锐化可以通过增加高频成分来实现；降噪则通常通过低通滤波去除高频噪声。傅立叶变换还能用于频域滤波，比如高斯滤波器可以有效地平滑图像，而拉普拉斯滤波器则有助于边缘检测。 总结来说，线性图像处理是通过卷积和傅立叶分析对图像进行数学操作，以改善图像质量或提取有用信息。本章的内容深入探讨了如何设计滤波核和优化算法，以提高处理效率并实现预期的图像处理目标。对于理解和实践数字信号处理在图像领域的应用，这些知识是至关重要的。