NG-DBSCAN：基于Spark的大规模聚类算法
需积分: 10 66 浏览量
更新于2024-09-11
收藏 1.08MB PDF 举报
"NG-DBSCAN：一种基于Spark的新型可扩展密度聚类算法"
这篇论文“NG-DBSCAN：适用于任意数据的可扩展密度聚类”由Alessandro Lulli、Matteo Dell’Amico、Pietro Michiardi、Laura Ricci等人撰写，来自意大利比萨大学、意大利国家研究委员会ISTI研究所、法国赛门铁克研究实验室和法国EURECOM。论文提出了NG-DBSCAN，一个针对任意数据和任何对称距离度量的近似密度基础聚类算法。该算法的分布式设计使其具有高度可扩展性，可以处理非常大的数据集。同时，其近似性质使它运行速度快，但仍然能够生成高质量的聚类结果。
1. 引言
聚类算法在数据分析中扮演着核心角色，通过无监督的方式将相似对象分组，帮助理解和解释数据。随着大数据时代的到来，对可扩展的聚类方法的需求日益增加。传统的DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法在处理大规模数据时可能会遇到性能瓶颈，而NG-DBSCAN正是为解决这一问题而提出的。
2. NG-DBSCAN算法原理
NG-DBSCAN基于Spark的并行计算框架，利用Spark的分布式内存计算能力，将数据划分到多个工作节点上进行并行处理。算法的关键步骤包括：数据预处理、核心对象识别、邻域探索和聚类生成。通过近似策略，NG-DBSCAN降低了计算复杂度，使得大规模数据集的处理成为可能。
3. 实验与评估
论文通过广泛的实验验证了NG-DBSCAN的性能和可扩展性。实验涉及真实世界和合成数据集，结果显示NG-DBSCAN不仅在运行时间上有显著优势，而且聚类质量接近于全精度的DBSCAN。这些实验结果支持了作者关于NG-DBSCAN的论点。
4. 应用场景
由于其高效和可扩展的特性，NG-DBSCAN适用于各种领域的大数据聚类问题，如社交网络分析、物联网(IoT)设备的分组、天文数据处理、市场细分和生物信息学等。
5. 总结
NG-DBSCAN是DBSCAN算法的一种创新改进，它结合了Spark的并行计算能力和近似算法的优势，为大数据环境下的聚类分析提供了新的解决方案。这种技术对于处理海量数据的科研人员和数据科学家来说，是一个强大的工具，有助于他们在保持高性能的同时，快速发现数据中的模式和结构。
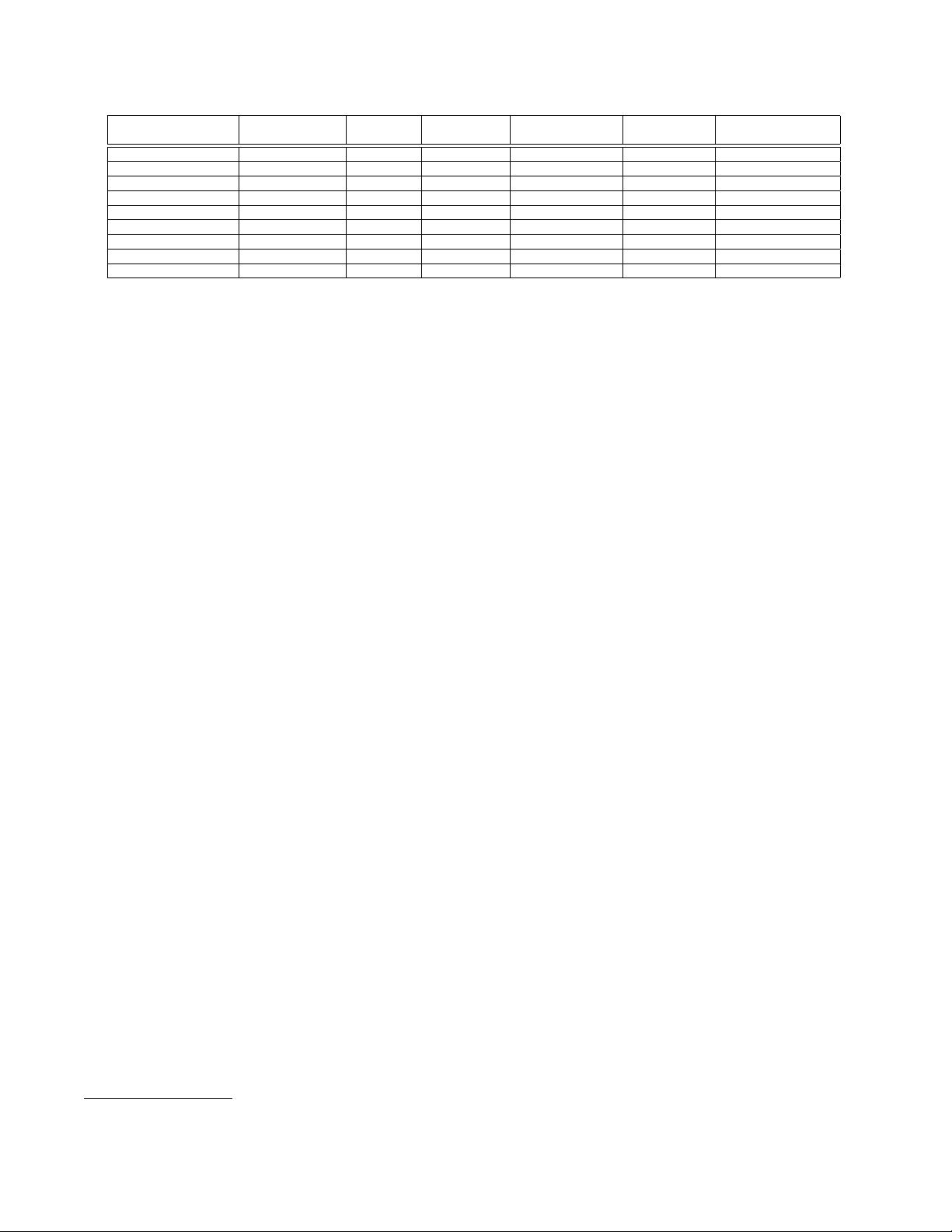
Table 1: Overview of parallel density-based clustering algorithms.
Name Parallel model
Implements
DBSCAN
Approximated Partitioner required
Data object
type
Distance function
supported
ρ-DBSCAN [12] single machine yes yes data on a grid point in n-D Euclidean
MR-DBSCAN [14] MapReduce yes no yes point in n-D Euclidean
SPARK-DBSCAN Apache Spark yes no yes point in n-D Euclidean
IRVINGC-DBSCAN Apache Spark yes no yes point in 2-D Euclidean
DBSCAN-MR [6] MapReduce yes no yes point in n-D Euclidean
MR. SCAN [30] MRNet + GPGPU yes no yes point in 2-D Euclidean
PARDICLE [25] MPI yes yes yes point in n-D Euclidean
DBCURE-MR [16] MapReduce no no yes point in n-D Euclidean
NG-DBSCAN MapReduce yes yes no arbitrary type arbitrary symmetric
which consider the input graph as given, is that our approach builds
the graph in its first phase; doing this efficiently is not trivial, since
some of the most common choices (such as ε-neighbor or k-nearest
neighbor graphs) require O(n
2
) computational cost for generic dis-
tance functions; our approximated approach obtains a substantial
cut on these costs.
2.4 Density-Based Clustering
for High-Dimensional Data
We conclude our discussion of related work with density-based
approaches suitable for text and high-dimensional data in general.
Tran et al. [28] propose a method to identify clusters with dif-
ferent densities. Instead of defining a threshold for a local density
function, low-density regions separating two clusters can be de-
tected by calculating the number of shared neighbors. If the num-
ber of shared neighbors is below a threshold, then the two objects
belong to two different clusters. Tran et al. report that their ap-
proach has high computational complexity, and the algorithm was
evaluated using only a small dataset (below 1 000 objects). In addi-
tion, as the authors point out, this approach is unsuited for finding
clusters that are very elongated or have particular shapes.
Zhou et al. [32] define a different way to identify dense regions.
For each object p, their algorithm computes the ratio between the
size of p’s ε-neighborhood and those of its neighbors, to distinguish
nodes that are at the center of clusters. This approach is once again
only evaluated and compared with DBSCAN in a 2D space.
3. NG-DBSCAN: APPROXIMATE AND
FLEXIBLE DBSCAN
NG-DBSCAN is an approximate, distributed, scalable algorithm
for density-based clustering, supporting any symmetric distance
function. We adopt the vertex-centric, or “think like a vertex” pro-
gramming paradigm, in which computation is partitioned by and
logically performed at the vertexes of a graph, and vertexes ex-
change messages. The vertex-centric approach is widely used due
to its scalability properties and expressivity [23].
Several vertex-centric computing frameworks exist [1, 13, 22]:
these are distributed systems that iteratively execute a user-defined
program over vertices of a graph, accepting input data from adja-
cent vertices and emitting output data that is communicated along
outgoing edges. In particular, our work relies on frameworks sup-
porting Valiant’s Bulk Synchronous Parallel (BSP) model [29], which
employs a shared nothing architecture geared toward synchronous
execution. Next, for clarity and generality of exposition, we gloss
over the technicalities of the framework, focusing instead on the
principles underlying our algorithm. Our implementation uses the
Apache Spark framework; its source code is available online.
1
1
https://github.com/alessandrolulli/gdbscan
3.1 Overview
Together with efficiency, the main design goal of NG-DBSCAN
is flexibility: indeed, it handles arbitrary data and distance func-
tions. We require that the distance function d is symmetric: that is,
d(x, y) = d(y, x) for all x and y. It would be technically possi-
ble to modify NG-DBSCAN to allow asymmetric distance, but for
clustering – where the goal is grouping similar items – asymmetry
is conceptually problematic, since it is difficult to choose whether
x should be grouped with y if, for example, d(x, y) is large and
d(y, x) is small. If needed, we advise using standard symmetriza-
tion techniques: for example, defining a d
0
(x, y) equal to the mini-
mum, maximum or average between d(x, y) and d(y, x) [11].
The main reason why DBSCAN is expensive when applied to
arbitrary distance measures is that it requires retrieving each point’s
ε-neighborhood, for which the distance between all node pairs needs
to be computed, resulting in O
n
2
calls to the distance function.
NG-DBSCAN avoids this cost by dropping the requirement of
computing ε-neighborhoods exactly, and proceeds in two phases.
The first phase creates the ε-graph, a data structure which will
be used to avoid ε-neighborhood queries: ε-graph nodes are data
points, and each node’s neighbors are a subset of its ε-neighbor-
hood. This phase is implemented through an auxiliary graph called
neighbor graph which gradually converges from a random starting
configuration towards an approximation of a k-nearest neighbor (k-
NN) graph by computing the distance of nodes at a 2-hop distance
in the neighbor graph; as soon as pairs of nodes at distance ε or less
are found, they are inserted in the ε-graph.
The second phase takes the ε-graph as an input and computes
the clusters which are the final output of NG-DBSCAN; cheap
neighbor lookups on the ε-graph replace expensive ε-neighborhood
queries. In its original description, DBSCAN is a sequential algo-
rithm. We base our parallel implementation on the realization that
a set of density-reachable core nodes corresponds to a connected
component in the ε-graph– the graph where each core node is con-
nected to all core nodes in its ε-neighborhood. As such, our Phase
2 implementation builds on a distributed algorithm to compute con-
nected components, amending it to distinguish between core nodes
(which generate clusters), noise points (which do not participate to
this phase) and border nodes (which are treated as a special case,
as they do not generate clusters).
NG-DBSCAN’s parameters determine a trade-off between speed
and accuracy, in terms of fidelity of the results to the exact DB-
SCAN implementation: in the following, we describe in detail our
algorithm and its parameters; in Section 5.4, we quantify this trade-
off and provide recommended settings.
3.2 Phase 1: Building the ε-Graph
As introduced above, Phase 1 builds the ε-graph, that will be
used to avoid expensive ε-neighborhood queries in Phase 2. We
159
剩余11页未读，继续阅读
2023-08-30 上传
2023-09-09 上传
2023-08-26 上传
2021-04-22 上传
2014-12-16 上传
2021-02-20 上传
2023-08-26 上传
2012-02-23 上传
2021-05-24 上传
