Logistic生长曲线模型预测：二分法与黄金分割法应用

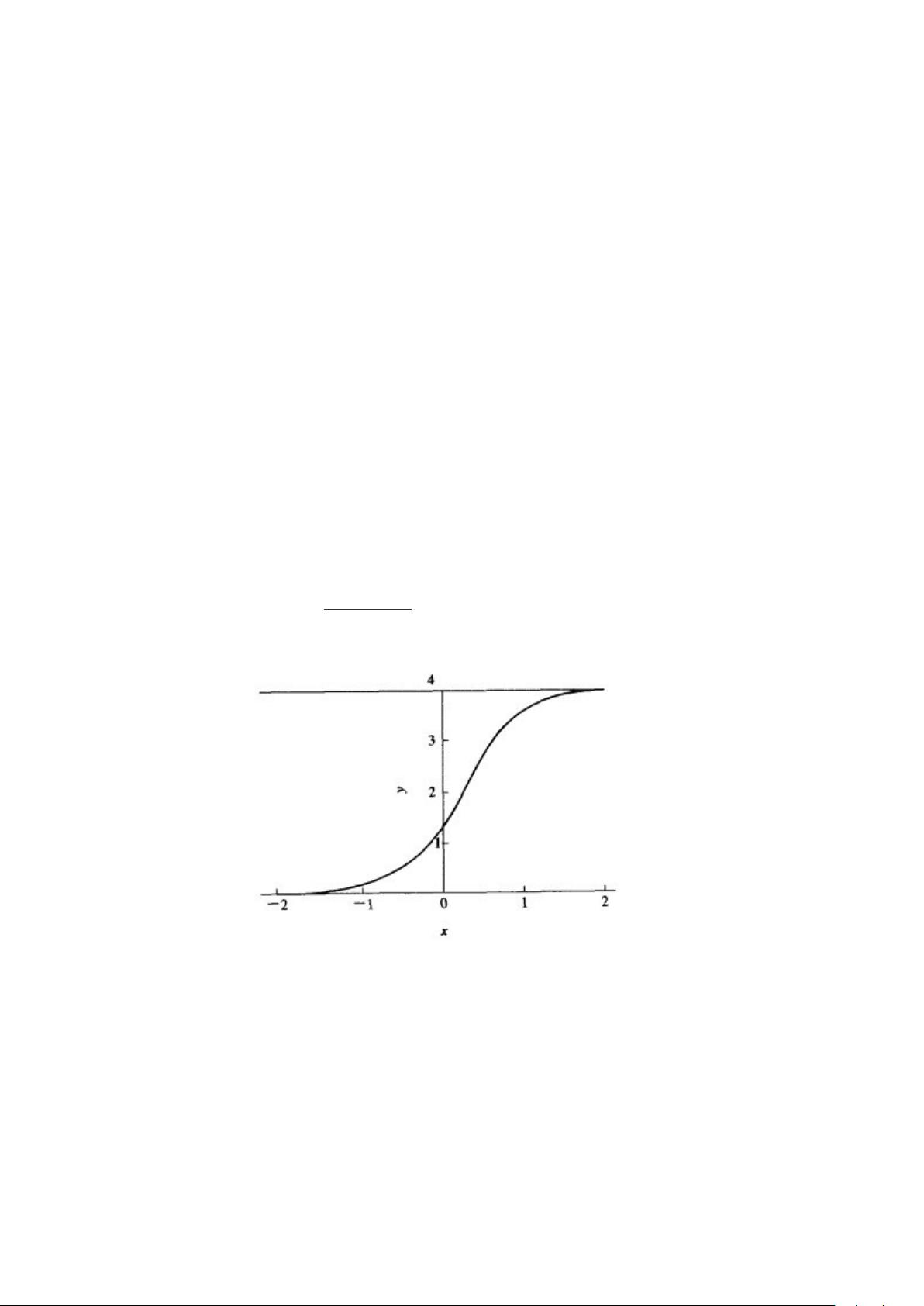
"Logistic生长曲线模型常用于预测随时间变化的事件，比如生物种群增长、市场渗透率等。这种模型假设数据遵循S型曲线，经历初期缓慢增长、中期快速上升和后期趋于饱和的三个阶段。Logistic模型的数学表达式为： \[ y = \frac{c}{1 + e^{-a(t - b)}} \] 其中，\( y \) 是时间 \( t \) 的观测值，\( c \) 是饱和值，\( a \) 决定了增长的速度，\( b \) 是达到最大增长率的一半时的时间点。 在模型参数估计过程中，可以采用非线性回归分析或特殊函数的最小二乘法。这里介绍了一种结合二分法和黄金分割法的优化回归方法来求解参数 \( a \)、\( b \) 和 \( c \)。首先，通过变换将模型简化为两变量形式，然后通过极值原理求解 \( A \) 和 \( B \) 的估计值。接下来，利用二分法和黄金分割法寻找最佳的 \( c \) 值。具体步骤如下： 1. 将Logistic模型转换为双变量形式，引入新变量 \( A \) 和 \( B \)。 2. 对新模型求极大值，找到 \( A \) 和 \( B \) 的最优解。 3. 使用二分法和黄金分割法迭代计算 \( c \) 的值，设定初始值和计算精度。 4. 实例中，大豆叶面指数与生育日数的关系通过这种方法拟合，得到高精度的模型，R²值和F检验值表明模型拟合良好。 5. 在MATLAB环境下，编写相应的算法函数 `logistic_fun` 进行编程和运行，以验证模型的有效性。 在MATLAB代码中，首先输入时间序列 \( t \) 和对应的观测值 \( y \)，然后对数据进行预处理。接着设定参数 \( c \) 的初始值、计算步长、精度等，最后编写算法实现并运行，得到拟合结果和相关统计指标。 Logistic生长曲线模型结合二分法和黄金分割法提供了一种有效预测随时间变化过程的方法，尤其适用于那些经历生长、发展和成熟三个阶段的现象。通过MATLAB等数值计算工具，可以方便地进行模型构建和参数估计，为实际问题提供科学的预测依据。"