伸展树(Splay)操作与平衡二叉树解析

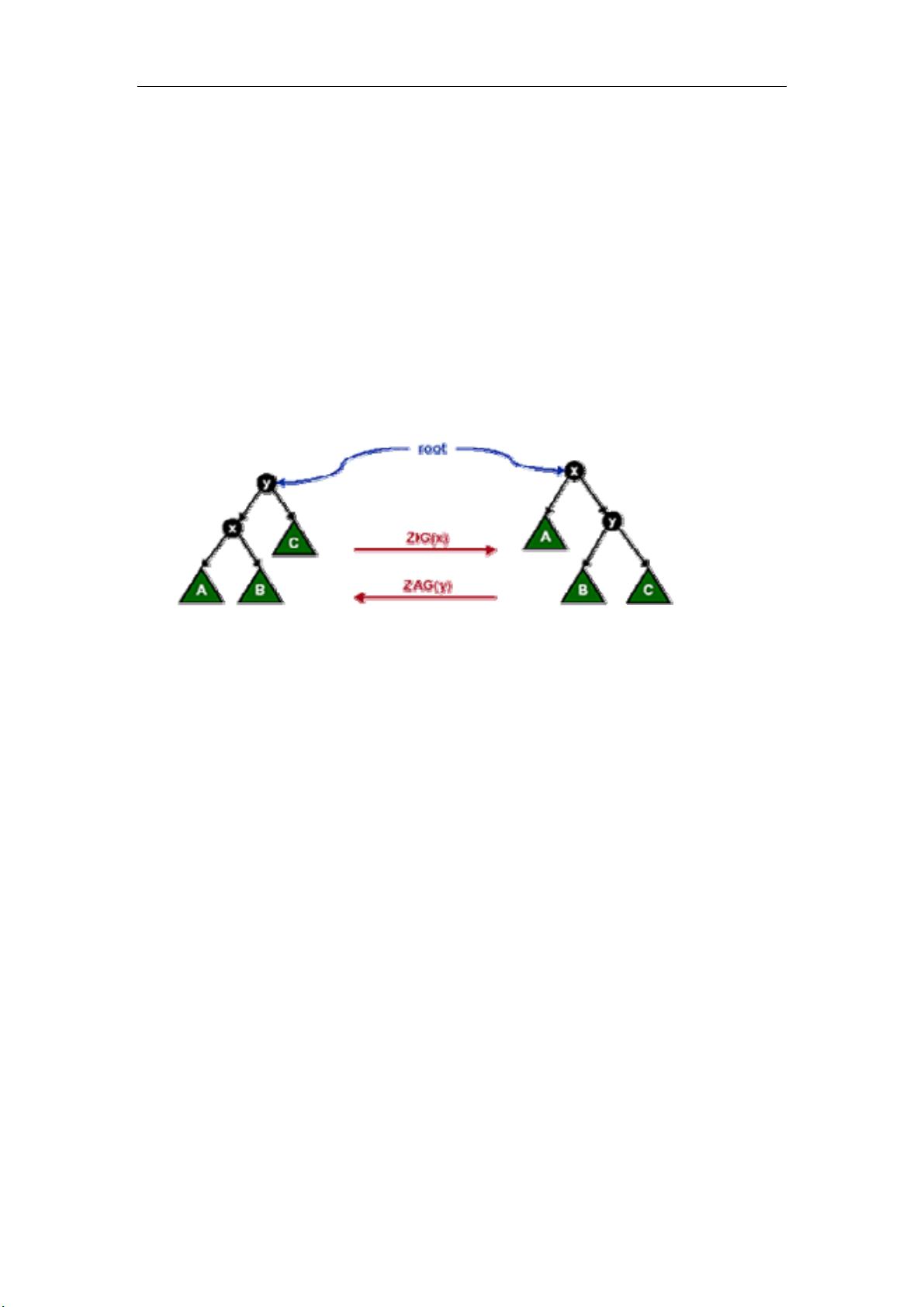
"伸展树(Splay Tree)是一种自调整的二叉搜索树，通过特定的伸展操作来保持树的平衡，以提高查询效率。本文主要关注伸展树的操作和特性，包括其与二叉搜索树、平衡二叉树如Treap和AVL树的对比，以及伸展树的初始化和伸展操作。\n\n二叉搜索树(BST)是一种基础数据结构，其左子树所有节点值小于根节点，右子树所有节点值大于根节点。在理想情况下，BST可以提供O(log N)时间复杂度的插入、删除和查找操作。然而，当树变得不平衡，例如由于特定数据分布导致的退化，性能可能会下降至O(N)。为了改善这种情况，引入了平衡二叉树。\n\n平衡二叉树(BBST)如AVL树和Treap，目的是维持树的平衡以确保高效操作。AVL树通过平衡因子确保左右子树高度差不超过1，提供稳定且高效的性能，但实现较为复杂。Treap则通过每个节点的随机优先级堆属性来保持平衡，虽然在大多数情况下效果良好，但平衡性仍可能不稳定。\n\n伸展树(Splay Tree)是本文的重点，它采用了一种不同的策略，即每次访问节点时，通过一系列旋转操作（如zig-zag和zig-zig）将该节点移至根部，称为\"伸展\"。这使得最近频繁访问的节点更靠近根部，减少了未来访问它们所需的时间。尽管单次操作可能不是O(log N)，但伸展树的平均时间复杂度通过平摊分析被证明是O(log N)，适用于多轮操作。\n\n伸展树的初始化通常涉及记录节点的子节点信息，以便在执行伸展操作时能够正确处理节点的移动。通过对称性的利用，可以简化代码实现，减少不必要的复杂性。伸展操作包括基本的旋转类型，如单旋和双旋，这些旋转用于在节点被访问后调整树的结构，使其更加平衡。\n\n总结来说，伸展树是一种动态优化的数据结构，通过自适应地调整树的形状来加速访问模式。虽然不如AVL那样严格平衡，但在实际应用中，尤其是在访问模式可预测或有热点的情况下，伸展树通常表现出良好的性能。"