Matlab中的数值拟合技术与最小二乘法

"在Matlab中数值拟合的应用主要探讨了如何使用Matlab进行数据拟合，特别是通过最小二乘法准则实现线性与非线性拟合。文档介绍了拟合的基本概念，特点以及常见的数据拟合准则，包括切比雪夫近似、极大化绝对偏差之和和最小二乘法。最小二乘法作为重点，用于确定使残差平方和最小的函数参数。通过示例展示了如何使用Matlab内置函数进行多项式拟合，并提供了具体的代码实现和拟合结果的可视化。" 在科学计算和工程领域，数据拟合是一项至关重要的任务，它涉及到从实验或观测数据中寻找合适的函数关系。Matlab作为一个强大的数值计算工具，提供了丰富的函数和方法来实现这一目标。在Matlab中，数值拟合可以帮助我们从有限的、可能存在噪声的数据中构建模型，以便于分析趋势、预测未来数据点或者理解物理过程。 拟合的基本思想是找到一个函数，这个函数能够最好地描述给定的数据点。在上述内容中，提到了拟合的两个关键特点：点数大于待求参数的个数，以及函数不一定通过所有数据点。这表明拟合的目标是在保证自由度的同时，尽可能地减少函数与数据点之间的偏差。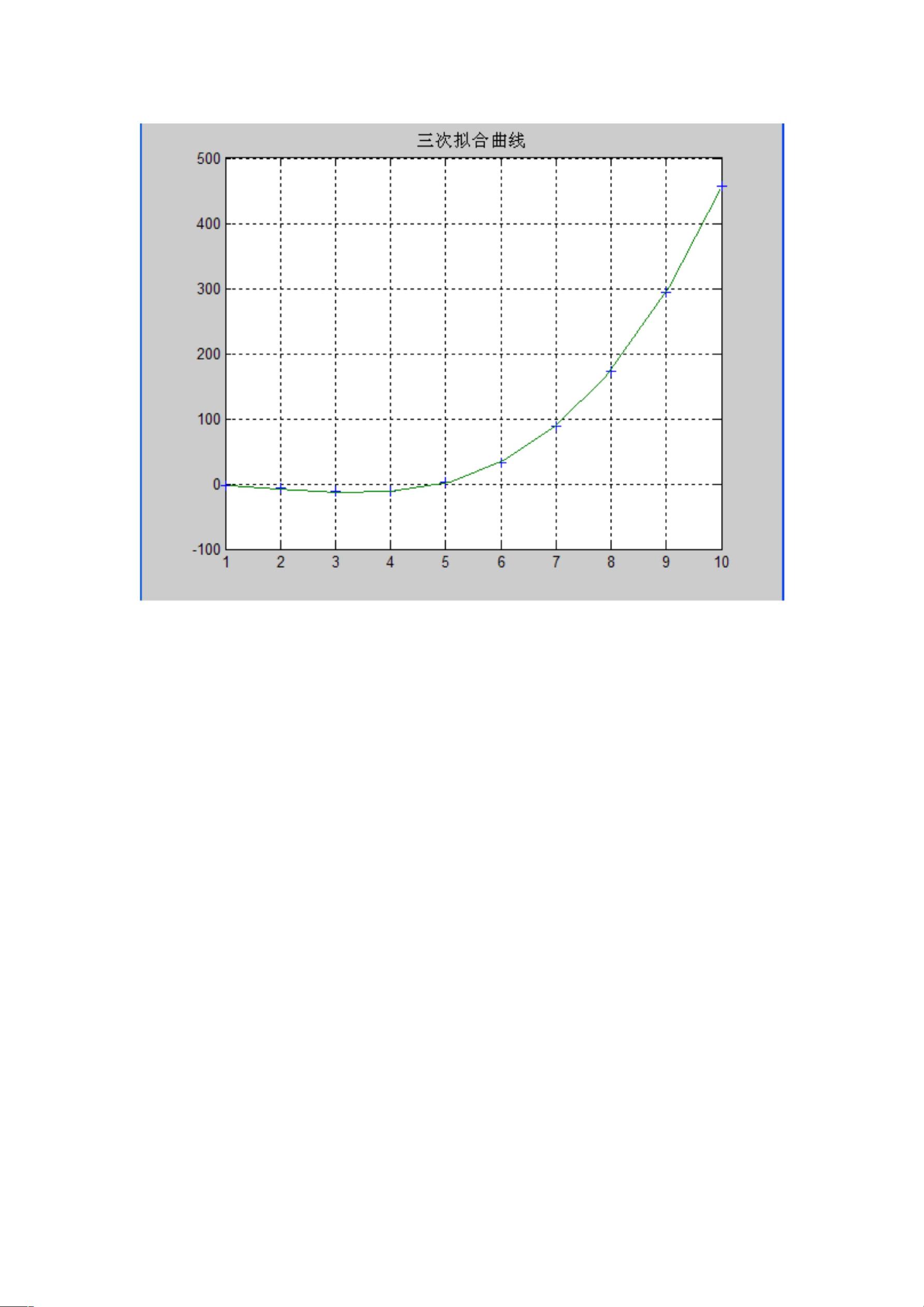 在选择拟合准则时，有多种选择，如切比雪夫近似、极大化绝对偏差之和和最小二乘法。最小二乘法是最常用的一种，它通过最小化残差平方和来寻找最佳拟合曲线。这种方法简单直观，而且在许多情况下能提供良好的结果。在Matlab中，可以通过`polyfit`函数进行线性或多项式拟合，例如在示例中使用的3次多项式拟合，代码如下： ```matlab x = 1:10; y = [0.9645, -5.4289, 3.4571, -0.4339]; % 示例数据 p = polyfit(x, y, 3); % 使用3次多项式进行拟合 fitted_y = polyval(p, x); % 计算拟合后的y值 ``` 拟合完成后，可以使用`plot`函数绘制原始数据点和拟合曲线，以可视化拟合效果。此外，Matlab还提供了诸如`lsqcurvefit`等函数，用于非线性拟合，它可以处理更复杂的形式，如指数、对数或用户自定义函数的拟合。 通过数值拟合，科学家和工程师能够从实验数据中提取有用的信息，建立数学模型，这对于理论研究、数据分析和预测具有重要意义。在Matlab中，这些功能使得数据处理变得高效且直观，为科学研究和工程应用提供了强大支持。