修复二叉搜索树：算法解析与实现

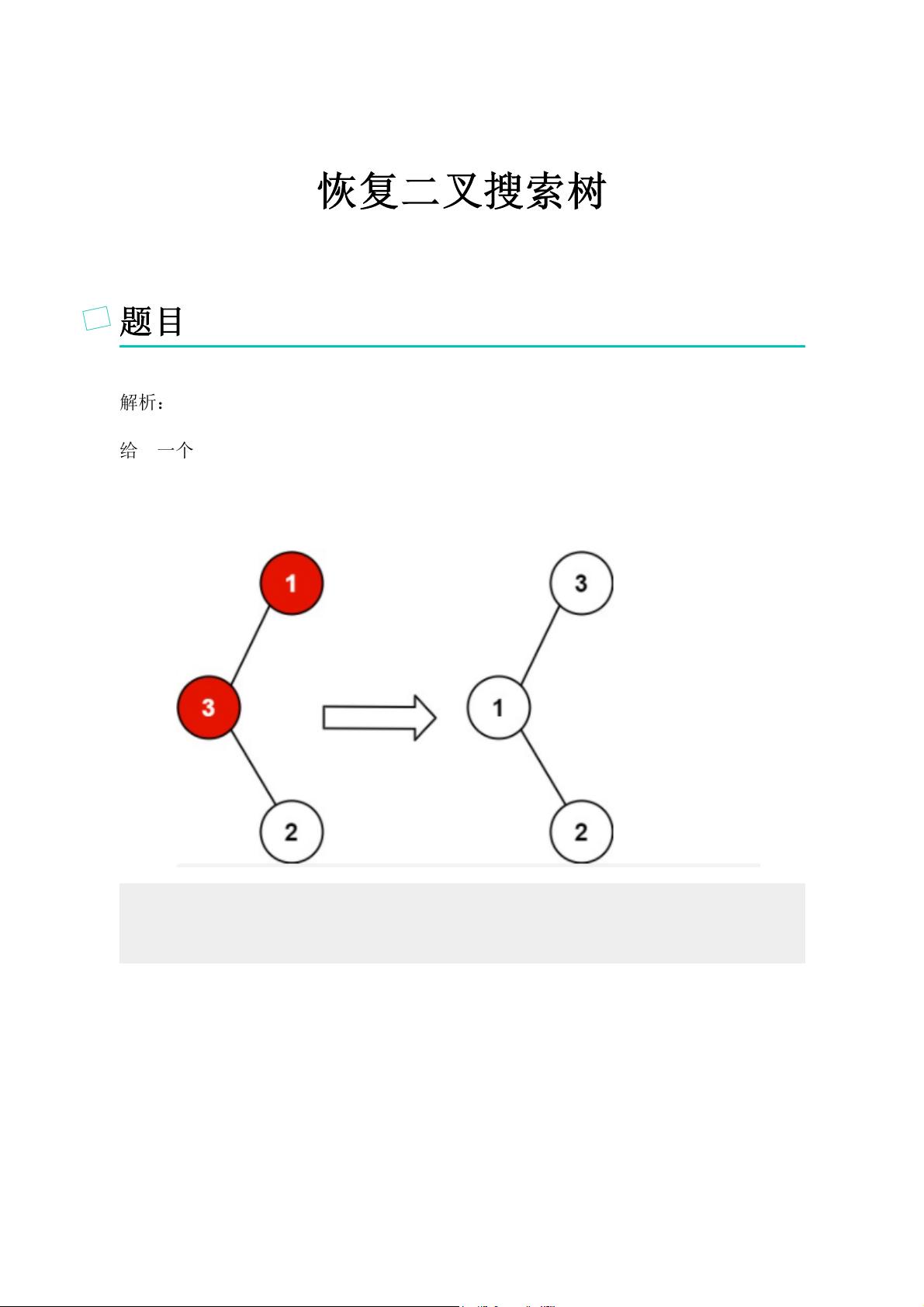
"恢复二叉搜索树的算法笔记" 在二叉搜索树（Binary Search Tree, BST）中，每个节点的值都必须满足左子树所有节点的值小于当前节点，右子树所有节点的值大于当前节点。这保证了BST在进行中序遍历时能够得到一个递增的序列。然而，当两个节点的值被错误地交换后，原有的递增性质将被破坏。本笔记将探讨如何恢复这样的二叉搜索树。 ### 问题阐述 给定一个二叉搜索树的根节点`root`，其中恰有两个节点的值被错误地交换。我们的任务是找出并交换这两个节点，使得二叉搜索树恢复其正确的结构。 ### 示例分析 例如，输入的二叉搜索树`root = [1, 3, null, null, 2]`。正确的中序遍历结果应该是升序序列，但因节点值交换，正确的顺序应该是`[1, 2, 3]`，而不是`[1, 3, 2]`。同样，对于`root = [3, 1, 4, null, null, 2]`，正确的中序遍历应为`[1, 3, 4, 2]`，但错误的值交换导致了`[1, 4, 2, 3]`。 ### 解决思路 - **方式1：显式中序遍历** 我们可以首先通过中序遍历得到一个递增序列。在遍历过程中，如果发现相邻的两个节点值不满足`ai < ai+1`，则找到了被交换的节点。对于不相邻的交换，会有两个位置不满足条件；对于相邻的交换，只有一个位置不满足条件。因此，我们只需要找到这些异常位置，然后回溯到原树，交换对应的节点值。 ### Java解题代码 ```java class Solution { public void recoverTree(TreeNode root) { List<Integer> nums = new ArrayList<>(); inorder(root, nums); int[] swapped = findTwoSwapped(nums); recover(root, 2, swapped[0], swapped[1]); } public void inorder(TreeNode root, List<Integer> nums) { if (root == null) { return; } inorder(root.left, nums); nums.add(root.val); inorder(root.right, nums); } // ...其余代码 } ``` 在这段代码中，`inorder`方法用于进行中序遍历，`findTwoSwapped`用于查找异常位置，而`recover`方法负责交换节点值以恢复树的正确状态。 ### 实现细节 - `findTwoSwapped`函数可能通过比较相邻元素来找到异常位置，找到最小值和最大值，这两个值即为被交换的节点。 - `recover`函数需要在原树上进行操作，找到这两个节点并交换它们的值，注意避免再次改变其他节点的顺序。 ### 总结 恢复二叉搜索树的关键在于利用其特性，即中序遍历得到的序列是递增的。通过遍历找到破坏递增性的异常，然后进行适当的交换，可以有效地恢复树的正确结构。这种方法不仅适用于Java，也可以应用到其他支持递归和数组操作的语言中。