AC算法：多模式匹配的高效解决方案

AC算法详解 AC算法，全称为Aho-Corasick算法，由Alfred V. Aho（编译原理经典教材《龙书》作者）和Margaret J. Corasick于1974年共同提出，与著名的KMP算法同时期诞生。它是一种高效的多模式匹配算法，针对给定的长度为n的文本和模式集合P={p1, p2, ..., pm}，能够在O(n)的时间复杂度内找出文本中所有模式的出现位置，显著优于当用KMP算法匹配多个模式时，时间复杂度会变为O(mn)的情况。 与KMP算法相似，AC算法也是在解决模式串前缀自包含问题的基础上发展起来的，但适用于处理多模式匹配。在KMP算法中，每个模式独立维护next跳转表，而在AC算法中，通过预处理模式集合，构建了一个全局的goto表，也称为状态转移自动机。这个goto表记录了从每个可能的当前状态出发，对应到下一个可能的字符位置，从而避免了逐个模式更新next表的开销。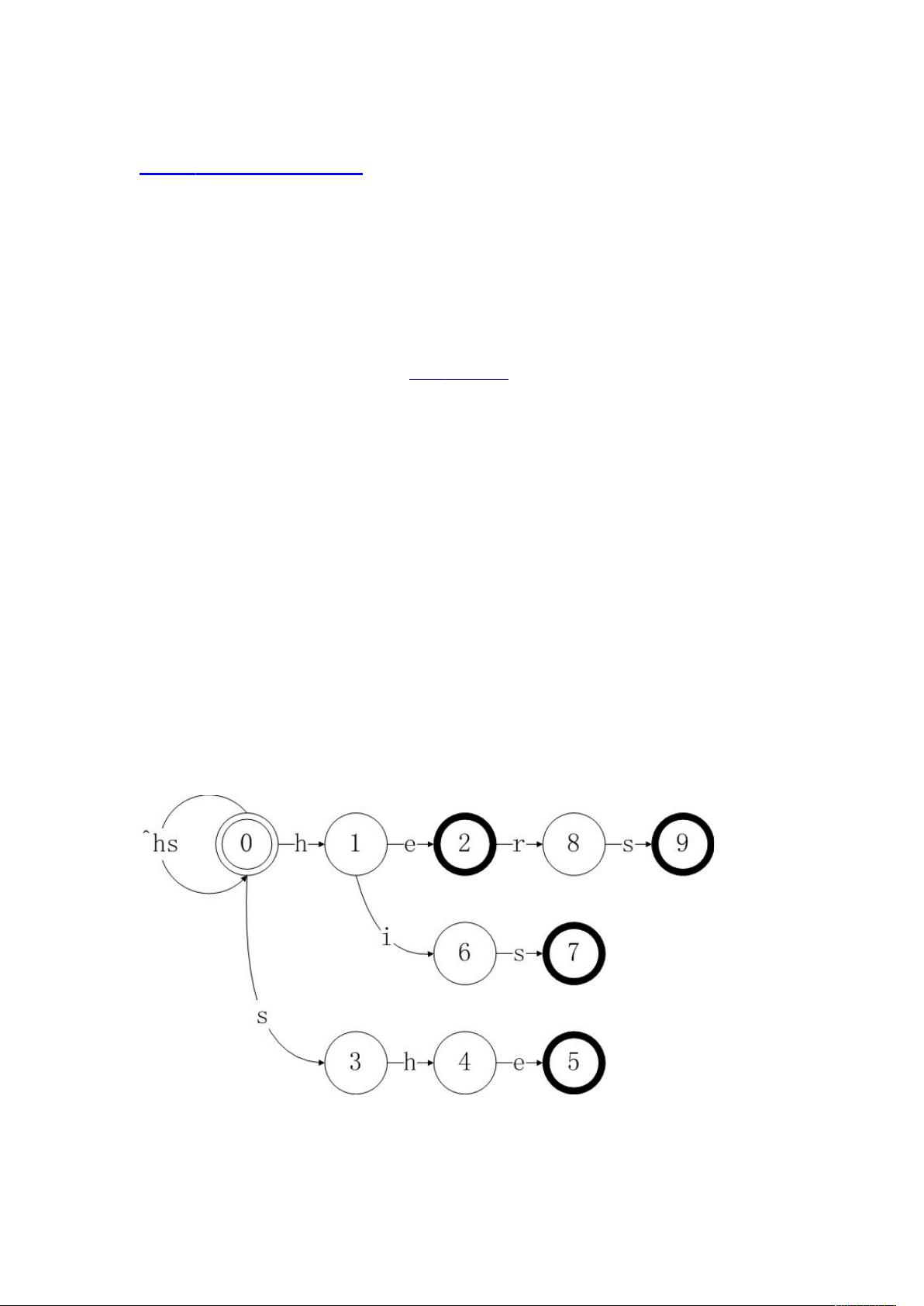 举例来说，以模式集合P={he, she, his, hers}中的模式he为例，即使在文本中的某个位置，遇到非前缀子串he，它实际上是模式(he)、(he)rs的前缀。AC算法利用这个特性，通过fail表（也称失配表），记录了每个状态可能从哪个失败的前缀状态继续匹配。当遇到匹配失败时，可以根据fail表快速转移到下一个可能的匹配位置，而不是回溯整个目标串。 AC算法的核心组成部分包括： 1. Goto表：这是模式集合P中所有模式的状态转移表，每个状态表示一个字符或模式结束的位置，表中的条目指示从当前状态出发，下一个字符应到达的状态。 2. Fail表：用于存储在模式匹配过程中，如果当前状态的字符不匹配，可以从之前的失败状态的失败位置继续搜索，这样可以避免回溯目标串。 3. Output表（可选）：用于记录每个模式首次出现的位置，便于输出结果。 通过这些表格的巧妙设计，AC算法能够在处理大规模模式集合时保持线性时间复杂度，显著提高了多模式匹配的效率。因此，AC算法在文本处理、搜索引擎优化等领域得到了广泛应用，尤其适合那些需要处理大量模式查找的应用场景。