4
Table I
TYPICAL LIE GROUPS USED IN 2D AND 3D MOTION, INCLUDING THE TRIVIAL R
n
. SEE THE APPENDICES FOR FULL REFERENCE
Lie group M, ◦ size dim X ∈ M Constraint τ
∧
∈ m τ ∈ R
m
Exp(τ ) Comp. Action
n-D vector R
n
, + n n v ∈ R
n
v − v = 0 v ∈ R
n
v ∈ R
n
v = exp(v) v
1
+v
2
v + x
circle S
1
, · 2 1 z ∈ C z
∗
z = 1 iθ ∈ iR θ ∈ R z = exp(iθ) z
1
z
2
z x
Rotation SO(2), · 4 1 R R
>
R = I [θ]
×
∈ so(2) θ ∈ R R = exp([θ]
×
) R
1
R
2
R x
Rigid motion SE(2), · 9 3 M =
R t
0 1
R
>
R = I
h
[θ]
×
ρ
0 0
i
∈ se(2)
ρ
θ
∈ R
3
exp
h
[θ]
×
ρ
0 0
i
M
1
M
2
R x+t
3-sphere S
3
, · 4 3 q ∈ H q
∗
q = 1 θ/2 ∈ H
p
θ ∈ R
3
q = exp(uθ/2) q
1
q
2
q x q
∗
Rotation SO(3), · 9 3 R R
>
R = I [θ]
×
∈ so(3) θ ∈ R
3
R = exp([θ]
×
) R
1
R
2
R x
Rigid motion SE(3), · 16 6 M =
R t
0 1
R
>
R = I
h
[θ]
×
ρ
0 0
i
∈ se(3)
ρ
θ
∈ R
6
exp
h
[θ]
×
ρ
0 0
i
M
1
M
2
R x+t
S
1
1
z(t)
T
1
S
1
= iR
T
z
S
1
z
v
^
= i! 2 iR
˙
z = z · i! /2 iR
1
v
^
= i! 2 iR
˙
z = i! 2 iR
!t
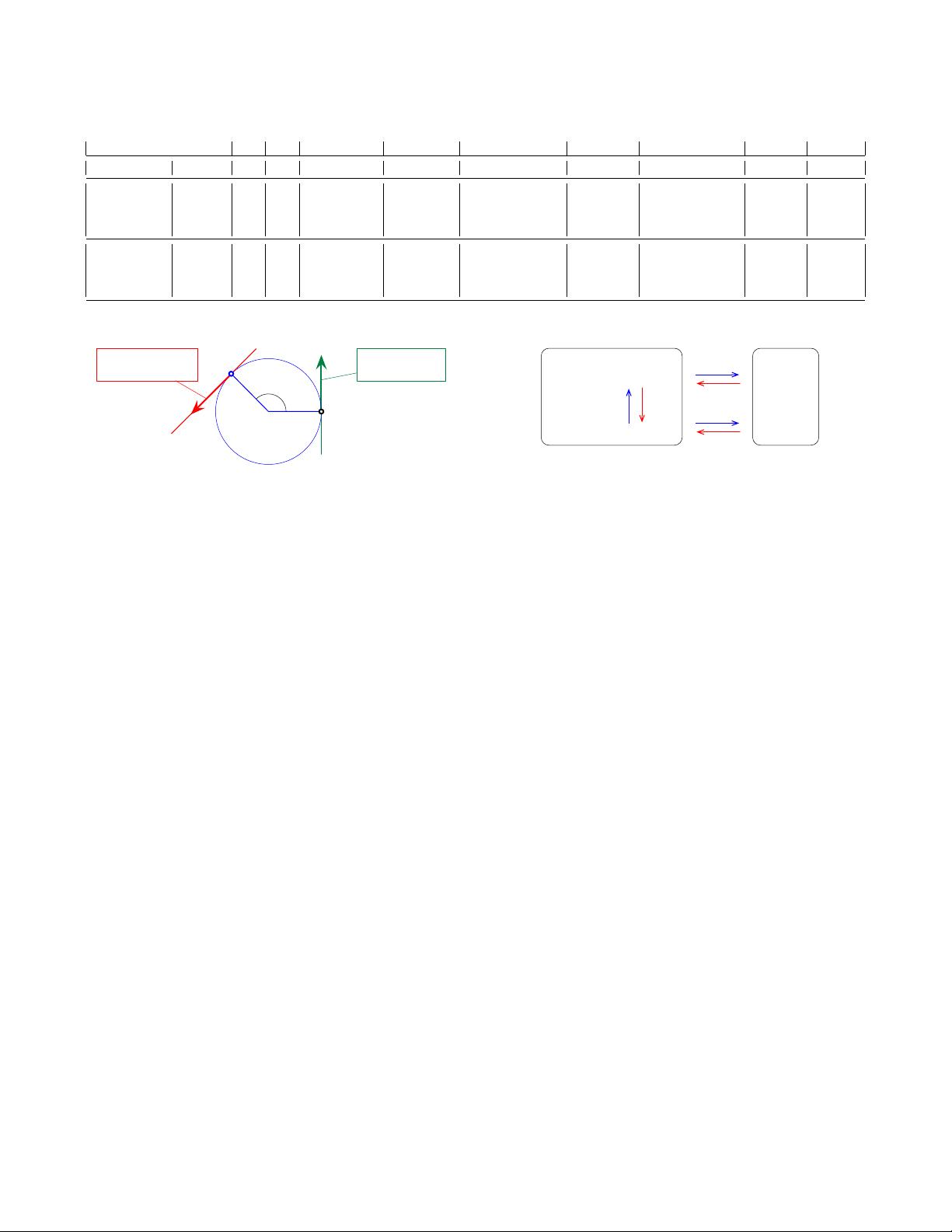
Figure 5. Let a point z ∈ S
1
move at constant rotation rate ω, z(t) =
cos ωt + i sin ωt. Its velocities when passing through 1 and z are in the
respective tangent spaces, T
1
S
1
and T
z
S
1
. In the case of T
z
S
1
, the velocity
is
˙
z = z iω = −ω sin ωt + iω cos ωt when expressed in the global
coordinates, and
z
v
∧
= iω when expressed locally. Their relation is given
by
z
v
∧
= z
−1
˙
z = z
∗
˙
z. In the case of T
1
S
1
, this relation is the identity
1
v
∧
=
˙
z = iω. Clearly, the structure of all tangent spaces is iR, which is
the Lie algebra. This is also the structure of
˙
z at the identity, and this is why
the Lie algebra is defined as the tangent space at the identity.
1) The Lie algebra m: The tangent space at the identity,
T
E
M, is called the Lie algebra of M, and noted m,
Lie algebra : m , T
E
M . (8)
Every Lie group has an associated Lie algebra. We relate the
Lie group with its Lie algebra through the following facts [5]
(see Figs. 1 and 6):
• The Lie algebra m is a vector space.
1
As such, its
elements can be identified with vectors in R
m
, whose
dimension m is the number of degrees of freedom of
M.
• The exponential map, exp : m → M, exactly converts
elements of the Lie algebra into elements of the group.
The log map is the inverse operation.
• Vectors of the tangent space at X can be transformed
to the tangent space at the identity E through a linear
transform. This transform is called the adjoint.
Lie algebras can be defined locally to a tangent point X,
establishing local coordinates for T
X
M (Fig. 5). We shall
denote elements of the Lie algebras with a ‘hat’ decorator,
such as v
∧
for velocities or τ
∧
= (vt)
∧
= v
∧
t for general
elements. A left superscript may also be added to specify the
precise tangent space, e.g.,
X
v
∧
∈ T
X
M and
E
v
∧
∈ T
E
M.
The structure of the Lie algebra can be found (see Exam-
ples 3 and 5) by time-differentiating the group constraint (3).
1
In a Lie algebra, the vector space is endowed with a non-associative
product called the Lie bracket. In this work, we will not make use of it.
X 2 M
log
exp
Log
Exp
(·)
_
(·)
^
Manifold
⌧
^
2 m
Lie algebra
⌧ 2 R
m
Vector
Tangent
T
E
M
Figure 6. Mappings between the manifold M and the representations of its
tangent space at the origin T
E
M (Lie algebra m and Cartesian R
m
). Maps
hat (·)
∧
and vee (·)
∨
are the linear invertible maps or isomorphisms (10–11),
exp(·) and log(·) map the Lie algebra to/from the manifold, and Exp(·) and
Log(·) are shortcuts to map directly the vector space R
m
to/from M.
For multiplicative groups this yields the new constraint
X
−1
˙
X +
˙
X
−1
X = 0, which applies to the elements tangent at
X (the term
˙
X
−1
is the derivative of the inverse). The elements
of the Lie algebra are therefore of the form,
2
v
∧
= X
−1
˙
X = −
˙
X
−1
X . (9)
2) The Cartesian vector space R
m
: The elements τ
∧
of
the Lie algebra have non-trivial structures (skew-symmetric
matrices, imaginary numbers, pure quaternions, see Table I)
but the key aspect for us is that they can be expressed as linear
combinations of some base elements E
i
, where E
i
are called
the generators of m (they are the derivatives of X around the
origin in the i-th direction). It is then handy to manipulate
just the coordinates as vectors in R
m
, which we shall note
simply τ . We may pass from m to R
m
and vice versa through
two mutually inverse linear maps or isomorphisms, commonly
called hat and vee (see Fig. 6),
Hat : R
m
→ m ; τ 7→ τ
∧
=
m
X
i=1
τ
i
E
i
(10)
Vee : m → R
m
; τ
∧
7→ (τ
∧
)
∨
= τ =
m
X
i=1
τ
i
e
i
, (11)
with e
i
the vectors of the base of R
m
(we have e
∧
i
= E
i
).
This means that m is isomorphic to the vector space R
m
—
one writes m
∼
=
R
m
, or τ
∧
∼
=
τ . Vectors τ ∈ R
m
are handier
for our purposes than their isomorphics τ
∧
∈ m, since they
can be stacked in larger state vectors, and more importantly,
2
For additive Lie groups the constraint X −X = 0 differentiates to
˙
X =
˙
X ,
that is, no constraint affects the tangent space. This means that the tangent
space is the same as the group space. See App. E for more details.
剩余16页未读，继续阅读
stanley.j
- 粉丝: 0
- 资源: 3
我的内容管理
展开
最新资源
- 计算机人脸表情动画技术发展综述
- 关系数据库的关键字搜索技术综述：模型、架构与未来趋势
- 迭代自适应逆滤波在语音情感识别中的应用
- 概念知识树在旅游领域智能分析中的应用
- 构建is-a层次与OWL本体集成：理论与算法
- 基于语义元的相似度计算方法研究：改进与有效性验证
- 网格梯度多密度聚类算法：去噪与高效聚类
- 网格服务工作流动态调度算法PGSWA研究
- 突发事件连锁反应网络模型与应急预警分析
- BA网络上的病毒营销与网站推广仿真研究
- 离散HSMM故障预测模型：有效提升系统状态预测
- 煤矿安全评价：信息融合与可拓理论的应用
- 多维度Petri网工作流模型MD_WFN：统一建模与应用研究
- 面向过程追踪的知识安全描述方法
- 基于收益的软件过程资源调度优化策略
- 多核环境下基于数据流Java的Web服务器优化实现提升性能
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
