组合逻辑电路复习：题型解析与真值表

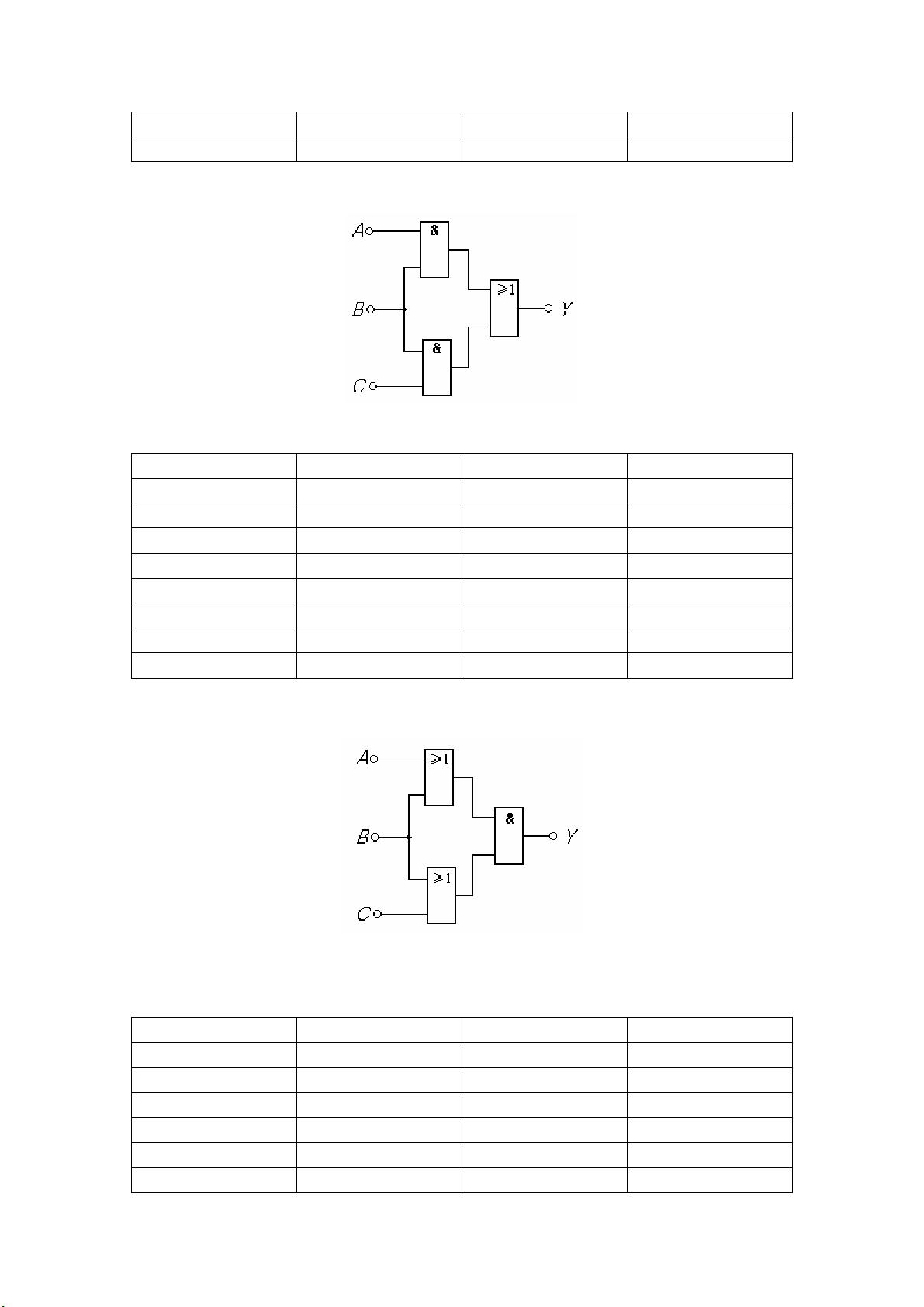
"电工与电子技术基础复习资料，包含组合逻辑电路的相关题目及答案，旨在帮助学生掌握逻辑表达式、电路化简及状态真值表的编写方法。" 在电工与电子技术基础的学习中，组合逻辑电路是一个重要的知识点。组合逻辑电路是由门电路（如与门、或门、非门等）组成的电路，其输出仅仅取决于当前输入信号的状态，不具有记忆功能。下面我们将详细解析这些题目中的知识点。 1. 组合逻辑电路的逻辑表达式：题目要求写出逻辑表达式，这通常涉及到布尔代数的基本运算，如与（AND）、或（OR）、非（NOT），以及异或（XOR）等。例如，一个电路可能包含A、B、C三个输入，逻辑表达式可能是Y = A'B + AC，表示Y是A的非与B的或再加上A和C的与的结果。 2. 逻辑表达式的化简：根据布尔代数定律，可以简化逻辑表达式，例如分配律（A(B+C) = AB + AC）、德摩根定律（A'+BC' = (A'+B')(A'+C')）等，以减少门电路的数量，提高电路效率。题目中给出的电路需要将原始表达式通过这些定律进行化简。 3. 状态真值表的构建：对于每个输入组合，状态真值表列出对应的输出值。例如，一个4变量的逻辑电路，真值表将有2的4次方（16）行，每一行对应一种输入组合及其相应的输出。题目要求列出状态真值表，这是验证逻辑表达式正确性的直观方法。 题目中列举了多个组合逻辑电路的例子，每个例子都要求写出逻辑表达式、化简并列出状态真值表。解题步骤通常是： a. 观察电路结构，识别出各个输入和输出信号。 b. 根据电路中门电路的连接方式，利用布尔代数规则写出逻辑表达式。 c. 对表达式进行化简，可以使用Karnaugh地图（K-Map）或其他简化方法。 d. 编制状态真值表，列出所有输入组合及其对应的输出。 通过这些练习，学习者能够巩固对组合逻辑电路的理解，掌握如何分析、设计和简化逻辑电路，这对于理解和应用数字逻辑系统至关重要。同时，熟悉这些基本操作也为后续学习更复杂的数字系统，如触发器、计数器、存储器等打下坚实基础。