图数据结构详解：邻接矩阵与邻接表

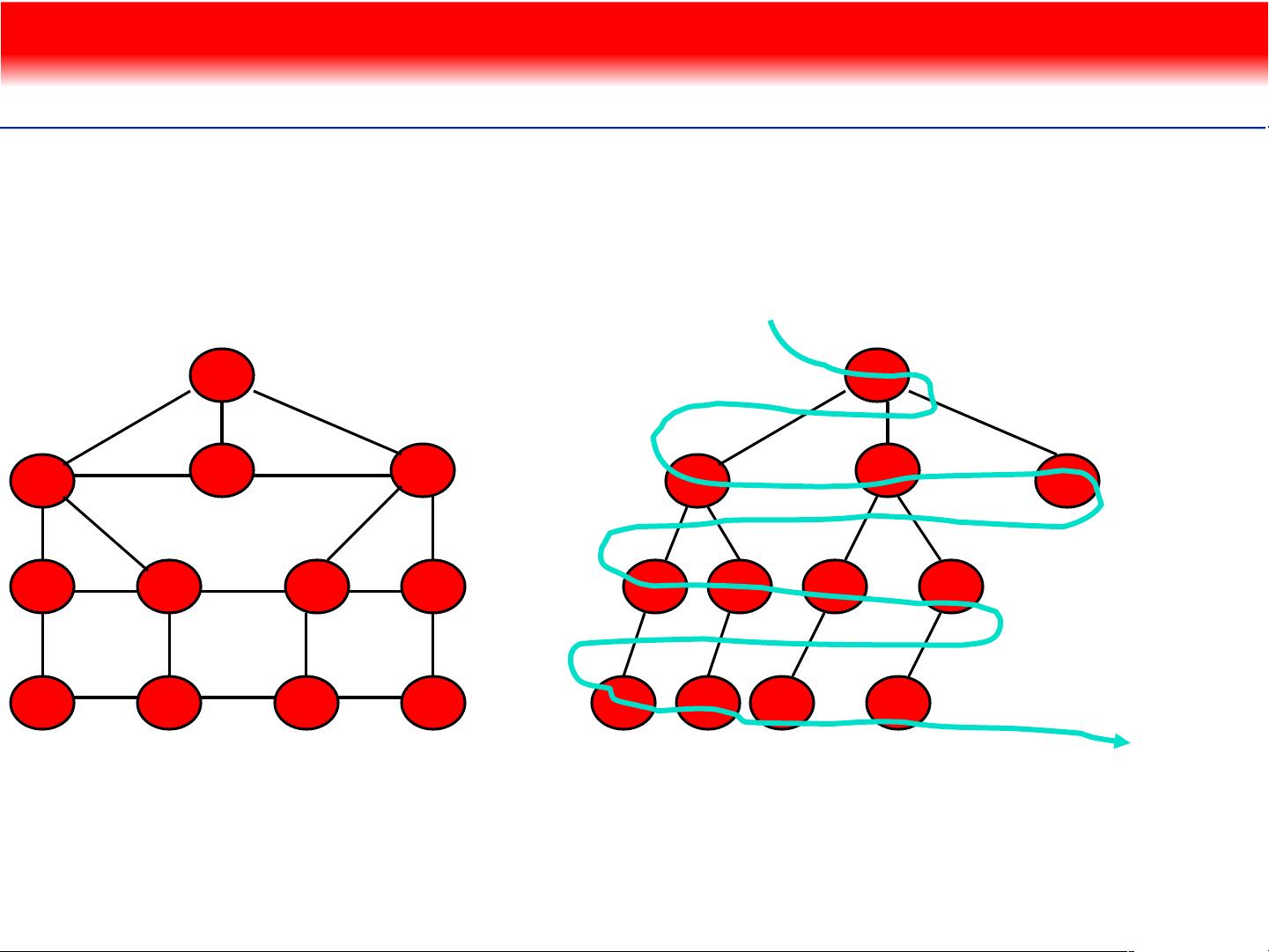
"本文主要介绍了数据结构中图的两种常见存储结构——邻接矩阵和邻接表，并讨论了它们各自的优缺点。同时，文中还涉及到了图的加权表示以及如何在邻接表中表示边和节点。" 在数据结构中，图是一种重要的非线性数据结构，用于表示对象之间的关系。图由顶点（节点）和边（连接顶点的线）组成，可以是无向的（边没有方向）或有向的（边有方向）。在实际应用中，为了高效地处理图的相关操作，如遍历、查找路径等，我们需要选择合适的存储结构。 1. 邻接矩阵 邻接矩阵是一种二维数组，用来存储图中顶点之间的连接信息。对于无权图，邻接矩阵的元素为0或1，表示对应顶点之间是否存在边。有向图的邻接矩阵是对称的，无向图则是对称的且每个非对角线元素都为0。加权邻接矩阵则进一步记录了边的权重，矩阵中的元素为边的权重值或特定标志表示无边。邻接矩阵的优点在于快速判断任意两个顶点之间是否有边，时间复杂度仅为O(1)，但其缺点是空间效率低，即使图中边的数量远小于顶点数量的平方，仍需要存储大量未使用的空间。 2. 邻接表 邻接表是另一种节省空间的图存储方式，尤其适用于稀疏图（边的数量远少于顶点数量的平方）。它包括结点表和边表两部分。结点表用数组或链表存储所有顶点，而边表则为每个顶点维护一个单链表，链表中的每个节点代表从该顶点出发的边。邻接表的优点在于其内存使用量等于顶点数加上边数，空间效率高，但确定两个顶点之间是否有边的时间复杂度最坏情况下为O(n)。对于无向图，同一边在邻接表中会被表示两次，造成空间浪费。此外，在有向图中查找所有进入某个顶点的边较为困难。 在邻接表中，每个节点通常包含两个字段：`data`用于存储顶点的实际数据，`firstarc`指向自该顶点出发的第一条边的边结点地址。边结点可能包含如`adjvex`（邻接顶点的索引）和`nextvex`（指向下一个边结点的指针）这样的字段，以构建单链表。 通过理解这两种存储结构，我们可以根据具体问题选择最适合的方法来处理图数据，优化算法性能。例如，在需要频繁查询边是否存在时，邻接矩阵可能更为合适；而在内存有限或图稀疏时，邻接表会是更好的选择。