Java实现的排序算法全面解析：插入排序、折半插入与希尔排序

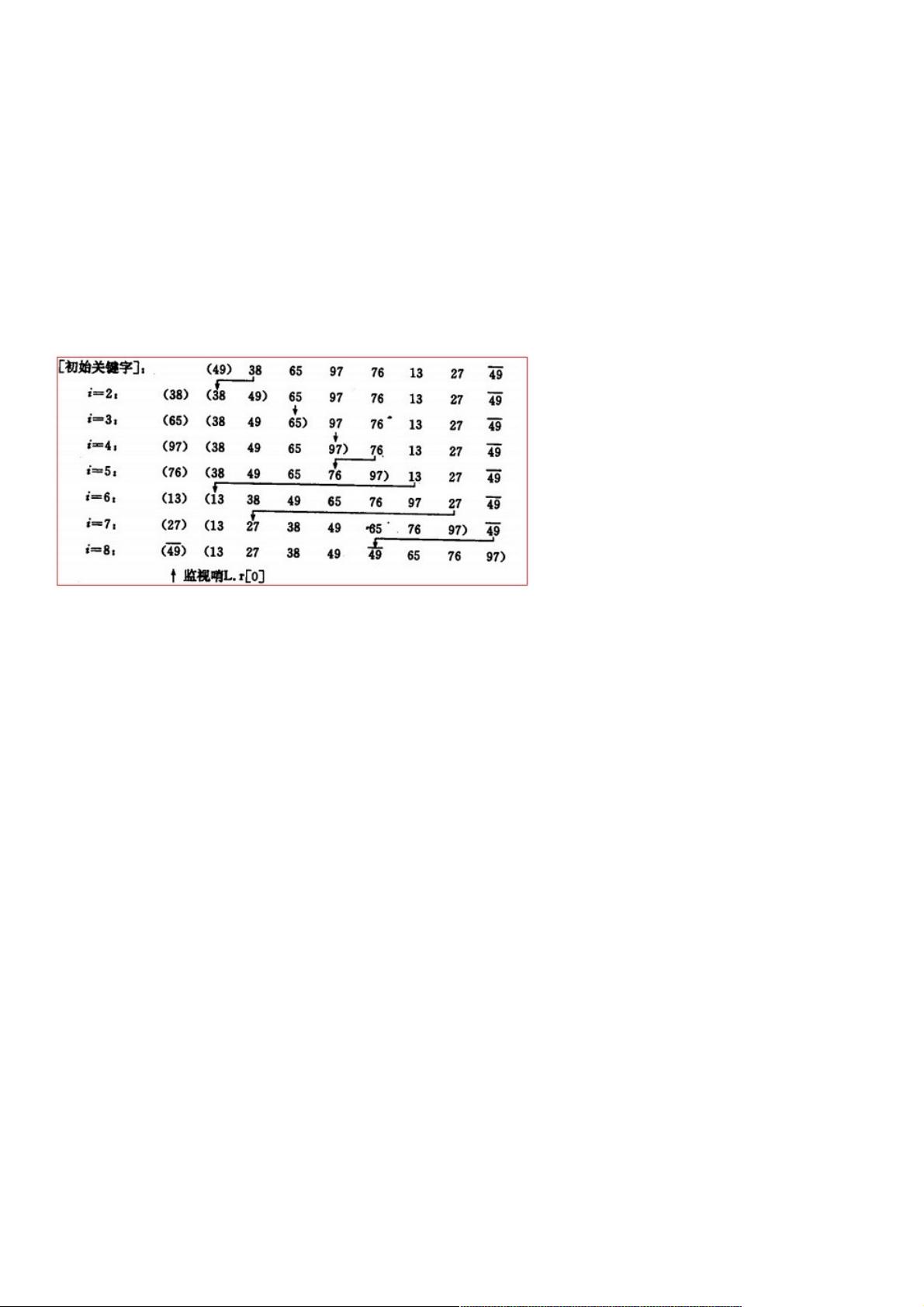
"这篇资源是关于各种排序算法的详细总结，特别关注Java语言的实现。内容包括直接插入排序、折半插入排序和希尔排序，详细阐述了每种算法的思想、时间复杂度、空间复杂度以及稳定性，并提供了Java代码示例。" 在排序算法的世界里，Java作为一种广泛应用的编程语言，其实现的排序算法具有广泛的学习价值。以下是针对这些排序算法的详细解释： 1. **直接插入排序**： - 直接插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。 - 时间复杂度：在最坏的情况下，当输入数组完全逆序时，直接插入排序的时间复杂度为O(n²)。 - 空间复杂度：由于排序过程中只需用到常数个额外空间，所以空间复杂度为O(1)。 - 稳定性：直接插入排序是稳定的，即相同元素的相对顺序不会改变。 2. **折半插入排序**： - 折半插入排序改进了直接插入排序的效率，通过二分查找找到插入位置，减少了比较次数。 - 虽然比较次数减少到了O(n㏒n)，但由于元素的移动次数仍然为O(n²)，所以总的时间复杂度仍然是O(n²)。 - 空间复杂度同样为O(1)。 - 稳定性：与直接插入排序一样，折半插入排序也是稳定的。 3. **希尔排序**： - 希尔排序是一种基于插入排序的快速排序方法，通过设置间隔序列（或称增量序列）来对原始数据进行分组，对每组进行插入排序，然后逐步减少间隔，直至间隔为1，进行最后一次排序。 - 时间复杂度：希尔排序的平均和最好情况下的时间复杂度比直接插入排序要低，但具体依赖于增量序列的选择，通常介于O(n)到O(n²)之间。 - 空间复杂度：由于仅使用了常数个额外空间，空间复杂度为O(1)。 - 稳定性：希尔排序不是稳定的排序算法，因为在不同的间隔序列中，相等元素可能交换位置。 以上三种排序算法在实际应用中各有优劣，根据数据特性选择合适的排序算法至关重要。在Java中，这些算法的实现可以帮助我们理解排序过程，并在需要的时候选择适当的排序方法。学习这些算法不仅可以提升编程技能，还能对算法分析和优化有深入的理解。