自动控制原理：根轨迹法与系统稳定性分析

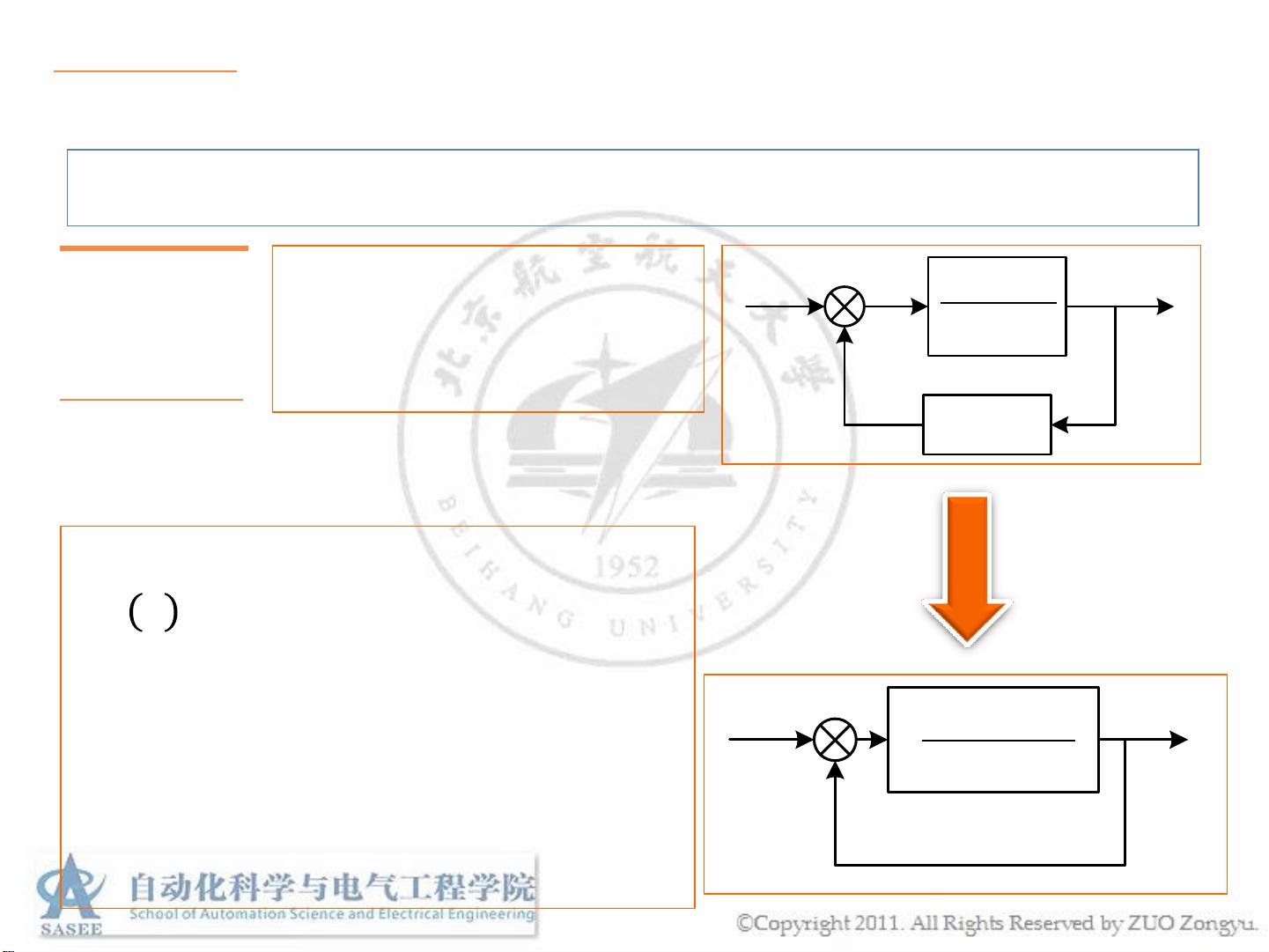
"自动控制原理：第四章 根轨迹法 -2.pdf" 自动控制原理是控制系统理论中的核心概念，主要研究如何分析和设计自动控制系统。在本资料中，重点关注的是根轨迹法，这是一种分析闭环系统稳定性的重要工具。根轨迹法通过绘制根轨迹图形，可以直观地了解系统动态特性和稳定性。 首先，资料提到了"广义根轨迹"，它适用于非单位负反馈系统。在这样的系统中，等效传递函数Gs和Hs被用来构建闭环传函Φ𝑠，即Φ𝑠=𝐺(𝑠)𝐻(𝑠)/(1+𝐺(𝑠)𝐻(𝑠))。闭环特征方程1+𝐺𝑠𝐻𝑠=0，它的根就是闭环系统的极点，这些极点决定了系统的动态响应。 接着，资料讨论了如何构造单位负反馈系统，并说明了构造出的新系统，即使零点和极点相同，也不能简单地进行对消，因为这会影响根轨迹的形状和位置。 在介绍"广义根轨迹"部分，资料给出了一个特征方程的例子：4(1+s/T)(s+K)=0，其中K是分离参数，T代表时间常数。这个方程可以用来求解闭环特征多项式，进而分析根轨迹的分布。 在"开环零点变化时的根轨迹"部分，资料通过实例分析了dT（时间常数）从0变化到无穷大时，根轨迹的变化情况。例如，对于给定的负反馈系统，闭环特征方程为Ds=5s^2+s+5Td*s+5=0，随着Td的变化，根轨迹的分支数、对称性、起始点、终止点以及渐近线的特性都可以被确定。计算得出的参数，如σa、φa和θp1、θp2，提供了根轨迹在实轴上的分布和角度信息。 本资料深入讲解了根轨迹法的基本概念和应用，通过实例展示了如何分析非单位负反馈系统和时间常数变化对根轨迹的影响，这对于理解和设计复杂控制系统的稳定性至关重要。