616 IEEE TRANSACTIONS ON COGNITIVE COMMUNICATIONS AND NETWORKING, VOL. 3, NO. 4, DECEMBER 2017
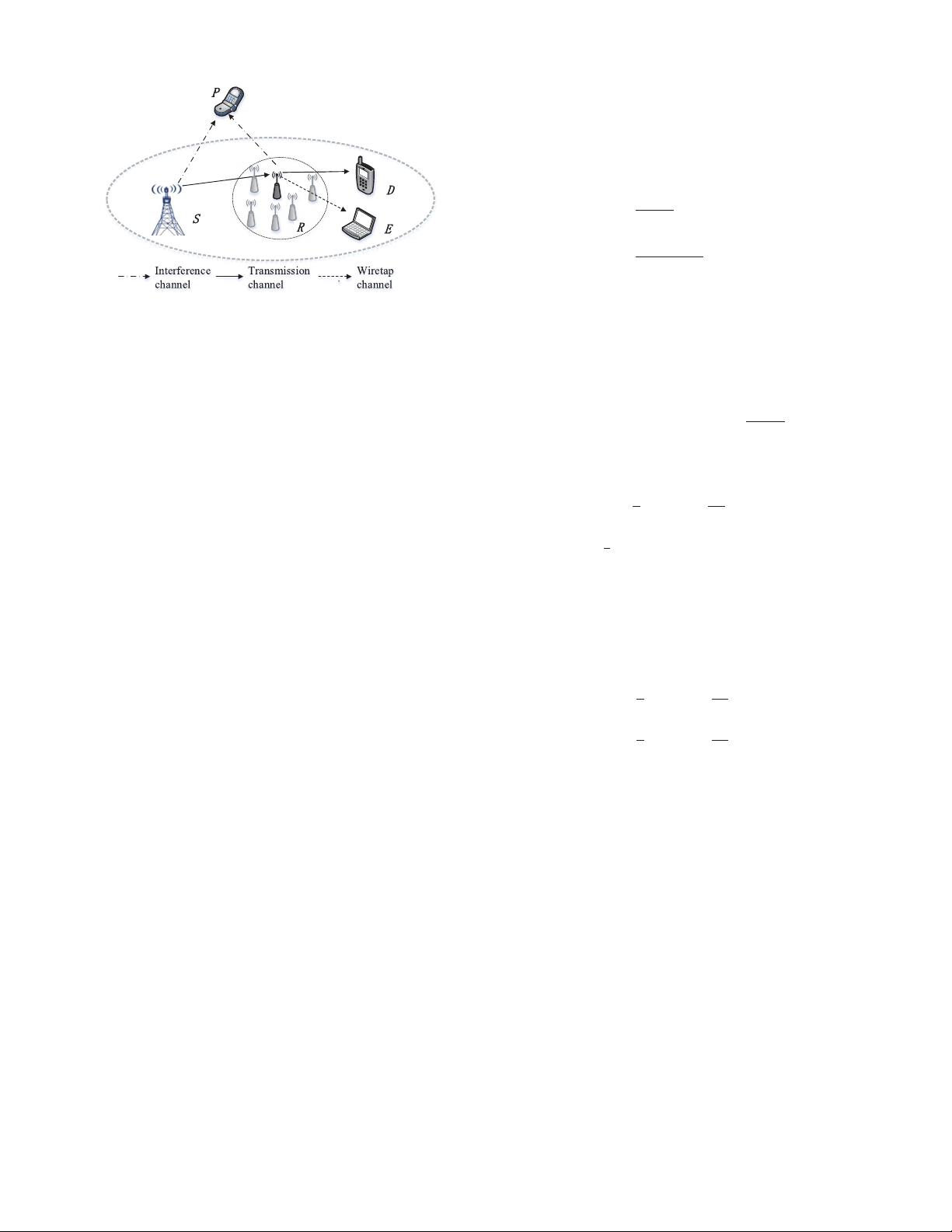
Fig. 1. System Model demonstrating a primary user (P), a secondary
user/source transmitter (S), a collection of relays (R), a desired destination
(D), and an undesired eavesdropper (E).
selection schemes in the underlay cognitive radio systems
experiencing i.n.i.d. Nakagami-m fading.
• Relative to [41]–[43] wherein only the maximum
interference power constraint is considered at the SU
source node, we consider more general conditions that
both the maximum interference power constraint and the
maximum transmit power constraint must be met at the
SU source node and all the relay nodes.
D. Structure
The rest of the paper is organized as follows. In Section II,
the system model considered in our work is described
and the ORS, SRS, and MRC schemes are presented. We
derive the exact and asymptotic closed-form expressions for
the SOP of the three different relay selection schemes in
Sections III and IV. In Section V, we present and discuss the
numerical results and the Monte-Carlo simulations. Finally,
Section VI concludes the paper.
II. S
YSTEM MODEL AND SECRECY CAPACITY
A. System Model
In this paper, we consider an underlay cognitive relay wire-
less network model, as shown in Fig. 1. It consists of a primary
user (P), a secondary transmitter (S), N secondary cooperative
relays (R
i
, 1 ≤ i ≤ N), one secondary destination (D), and an
eavesdropper (E). Following [15]–[17], we consider that the
directly links between S and D/E are unavailable due to severe
shadowing and path-loss, and communication can be estab-
lished only via relays. We assume that all nodes are equipped
with a single antenna and the relays utilizing two adjacent
time slots are employed. In the first time slot, S broadcasts
its signal to the relays that attempt to decode their received
signals. In the second time slot, only the optimal relay, which
is selected from the successful decode relay set, forwards the
decoded outcome to D, and E may overhear the confiden-
tial information, where a two slot protocol has been utilized,
based on numerous works in the available literature [18]–[21].
All the channels are assumed to experience i.n.i.d. quasi-static
Nakagami-m fading with fading parameters m
j
and average
channel power gains
j
, where j ∈ (SP, SR
i
, R
i
P, R
i
D, R
i
E).
The thermal noise at each receiver is modeled as additive white
Gaussian noise (AWGN) with variance σ
2
.
The probability density function (PDF) and the cumula-
tive distribution function (CDF) of the channel gains can be
expressed by
f
Y
j
(
y
)
=
λ
j
m
j
m
j
y
m
j
−1
exp
−λ
j
y
, (1)
F
Y
j
(
y
)
=
ϒ
m
j
,λ
j
y
m
j
, (2)
where λ
j
= m
j
/
j
, (·) is the gamma function, as
defined by [44, eq. (8.310)] and ϒ(a, x) =
x
0
exp(−t)t
a−1
dt
is the lower incomplete gamma function, as defined
by [44, eq. (8.350.1)].
Using [44, eq. (8.352.1)], the CDF of Y
j
is rewritten as
F
Y
j
(
y
)
= 1 − exp
−λ
j
y
m
j
−1
n=0
λ
j
y
n
n!
. (3)
The channel capacity between S to the ith relay is given by
C
SR
i
=
1
2
log
2
1 +
P
S
σ
2
Y
SR
i
, (4)
where the factor
1
2
in front of log(·) arises from the fact
that relays operate in half-duplex mode and two time slots
are required to complete the transmission of S to D via
R
i
[15], [37]. P
S
is the transmit power at S, Y
SR
i
=|h
SR
i
|
2
,
and h
SR
i
is the channel fading coefficients between S and R
i
.
Similarly, the channel capacity from the ith relay to D/E
can be given by
C
R
i
D
=
1
2
log
2
1 +
P
i
σ
2
Y
R
i
D
, (5)
C
R
i
E
=
1
2
log
2
1 +
P
i
σ
2
Y
R
i
E
, (6)
respectively, where P
i
is the transmit power at the ith relay,
Y
R
i
D
=|h
R
i
D
|
2
, Y
R
i
E
=|h
R
i
E
|
2
, h
R
i
D
and h
R
i
E
are the channel
fading coefficients between R
i
and D/E, respectively.
According to underlay cognitive radio transmission, the
transmit power at S and relays must be limited at a given
threshold to guarantee a reliable communication at P [10].
Due to the maximum interference power constraint and the
maximum transmit power constraint, the transmit power at S
and ith relay are strictly constrained by
2
P
S
= min
(
P
max
, P
I
/Y
SP
)
, (7)
P
i
= min
P
max
, P
I
/Y
R
i
P
, (8)
respectively, where P
max
is the maximal transmit power at
S and all the relays, and P
I
is the maximum tolerated
interference power at P.
2
As similar to [32]–[43], it is assumed that source and relay nodes are with
perfect CSI in our work. However, considering that the channel estimation is
not perfect and always suffers from estimation errors, our derived results are
optimistic compared to the practical ones. Analyzing the secrecy performance
of CRN with outdated CSI is an interesting topic and will be part of our future
work.









