林轩田《机器学习基石》笔记：线性回归原理与最小二乘法应用

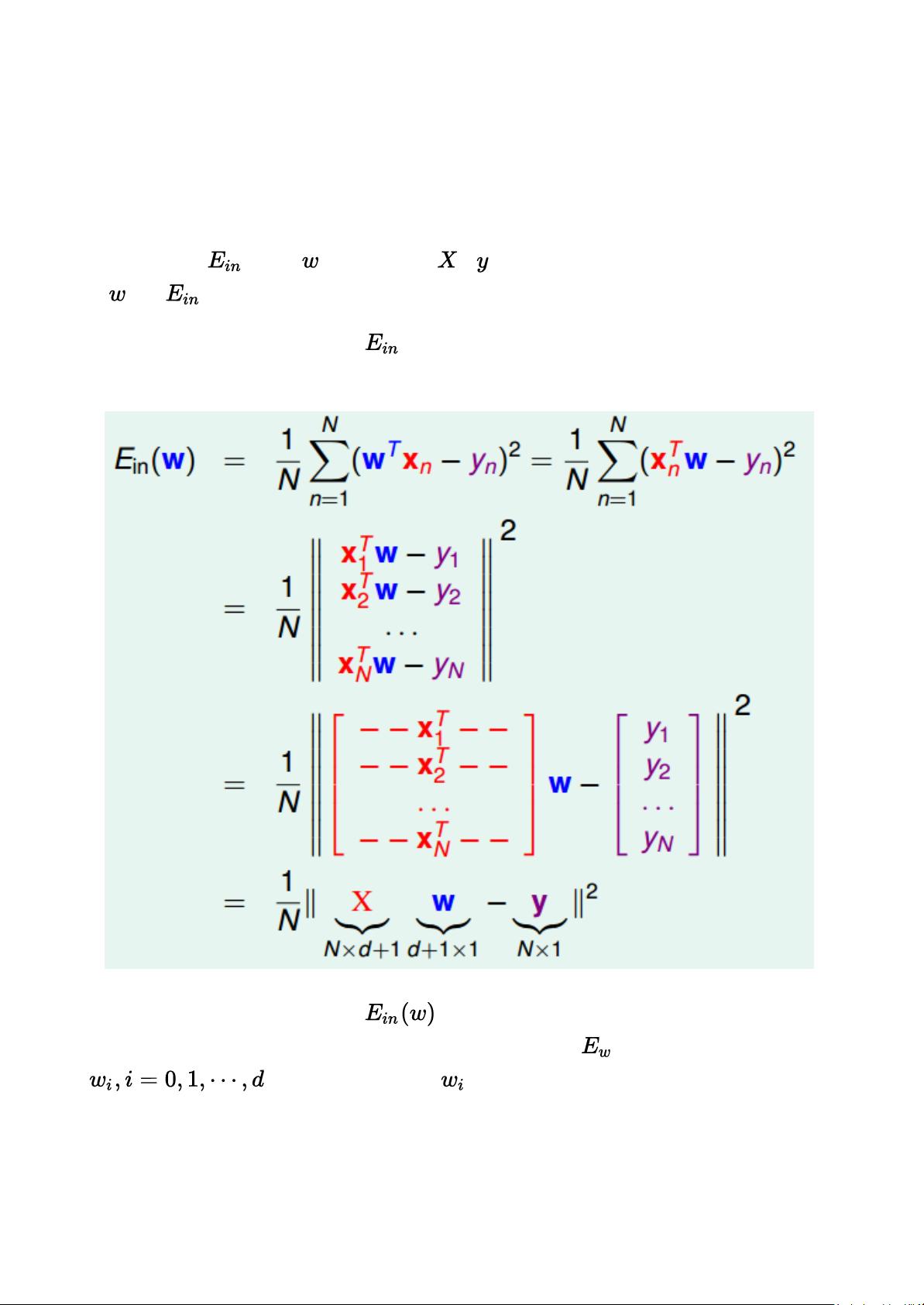
林轩田在《机器学习基石》课程的第九章中深入探讨了线性回归这一核心概念。他首先回顾了在噪声环境中VCBound理论的应用，并强调了不同误差测量方法的重要性，如最小二乘法，它是线性回归中最常用的一种。 在本节课程中，林轩田通过信用卡额度分配问题来引入线性回归的实际应用。用户特征集被表示为一个d维空间，加入一个常数项后，形成了d+1维的输入向量。线性回归的目标是找到一个权重向量w，使得预测函数Hypothesis（记为hθ）与实际观测值y之间的残差误差最小化。线性回归预测函数的值域是整个实数空间，与线性分类有所区别。 最小二乘法作为误差测量的基础，它的目的是寻找使总平方误差（如平方误差和）最小化的权重。尽管线性最小二乘问题有closed-form解，即可以通过一次求解得到权重，而非线性问题则通常需要迭代方法。课程中提到的权重向量w的计算公式利用了矩阵运算，特别是对目标函数J(w)进行偏导数分析，当偏导数为零时，达到了最优解。 具体来说，通过矩阵转换，将权重向量w和特征矩阵X的关系表达为矩阵形式，然后利用伪逆矩阵（记作X⁺，维度为(d+1)xN），得出权重向量w = X⁺y。这里的X⁺是X的伪逆，它在解决欠定或奇异矩阵问题时发挥关键作用。 值得注意的是，当遇到欠定问题（特征矩阵的列数小于行数）时，X可能没有逆矩阵，但伪逆的存在确保了线性回归问题的可解性。本节内容详细介绍了线性回归问题的数学基础、求解策略以及权重向量的推导过程，这些都是理解和实践机器学习算法不可或缺的部分。