字符串算法:周期,边框与KMP
需积分: 50 146 浏览量
更新于2024-07-16
收藏 157KB PDF 举报
"该资源是一份关于字符串算法的讲义,由金策在清华大学交叉信息研究院讲解,主要涵盖了字符串的基本概念、周期与边界、KMP算法以及后缀数组和LCP查询等内容。"
字符串算法是计算机科学中的一个重要领域,尤其在算法竞赛、ACM/IOI、ICPC等比赛中扮演着关键角色。讲义首先介绍了字符串的基本概念,包括字符串的定义(s[1..n],|s|=n),字符集(常见的是26个小写字母),子串(s[i..j]),以及前缀(pre(s, x))和后缀(suf(s, x))。
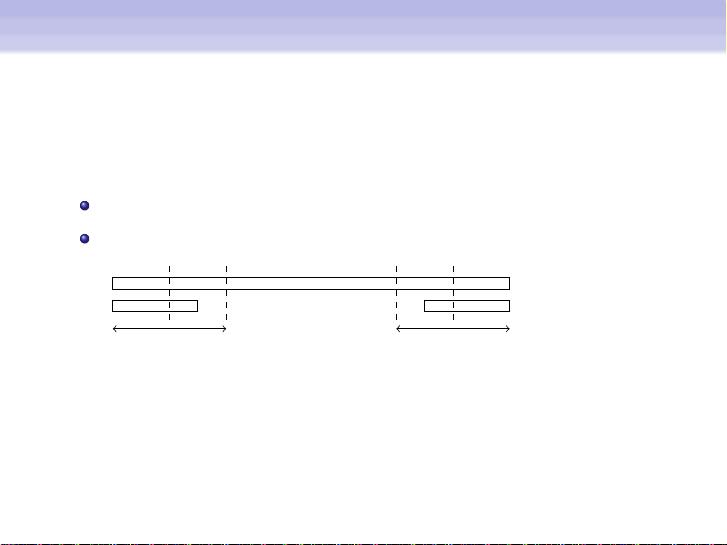
接着,讲义讨论了字符串的周期(period)和边界(border)。周期是指字符串中的某个长度p,使得从任意位置开始的p个字符都与下一个p个字符相同。例如,字符串"abaaaba"的周期有4、6和7。边界则是指字符串的前缀与后缀相等的部分,一个字符串的前缀是它的border当且仅当它的长度是字符串长度减去一个周期。因此,"aba"是"abaaaba"的一个border,对应周期为3。
讲义中提到了KMP算法,这是一类用于字符串匹配的高效算法。KMP算法能在O(n)的时间复杂度内构造出失败函数(fail数组),该函数记录了前缀s[1..i]的最大border长度。通过fail数组,可以快速找出字符串的所有border长度。
此外,讲义还涉及到了后缀数组和最长公共前后缀(LCP)查询。后缀数组是在O(n log n)的时间复杂度下预处理得到的,它允许我们在常数时间内找到两个子串的LCP和LCS。对于具有周期p的字符串s,其自身与偏移p后的子串的LCP等于n-p。通过后缀数组,我们能迅速找出具有特定周期p的子串的最长长度。
最后,讲义提到了周期性引理(Periodicity Lemma),它指出如果一个字符串有周期p和q,那么它们的最大公约数(gcd(p, q))也是字符串的周期。这意味着字符串的周期具有一定的组合性质。
总结起来,这份讲义深入浅出地介绍了字符串算法中的基本概念和重要算法,对于理解和掌握字符串处理的技巧非常有帮助。无论是对于初学者还是有一定基础的程序员,都能从中受益。
399 浏览量
109 浏览量
2022-01-23 上传
2019-07-05 上传
2021-03-25 上传
2024-01-21 上传
2022-01-12 上传
167 浏览量
wh653
- 粉丝: 1
- 资源: 5