小波变换深入解析:母小波与父小波在信号处理中的作用
需积分: 10 32 浏览量
更新于2024-07-17
收藏 1.89MB PDF 举报
"这篇文档是《小波变换和motion信号处理》系列的第二部分,深入探讨小波变换的原理和特性。文档介绍了小波变换的基础,包括母小波、父小波以及它们如何构建小波基。此外,还强调了小波变换的正交性、二维特性和定位能力。接下来,文档将详细解释完整的小波展开形式,尺度函数的作用,以及多解析度分析的概念。"
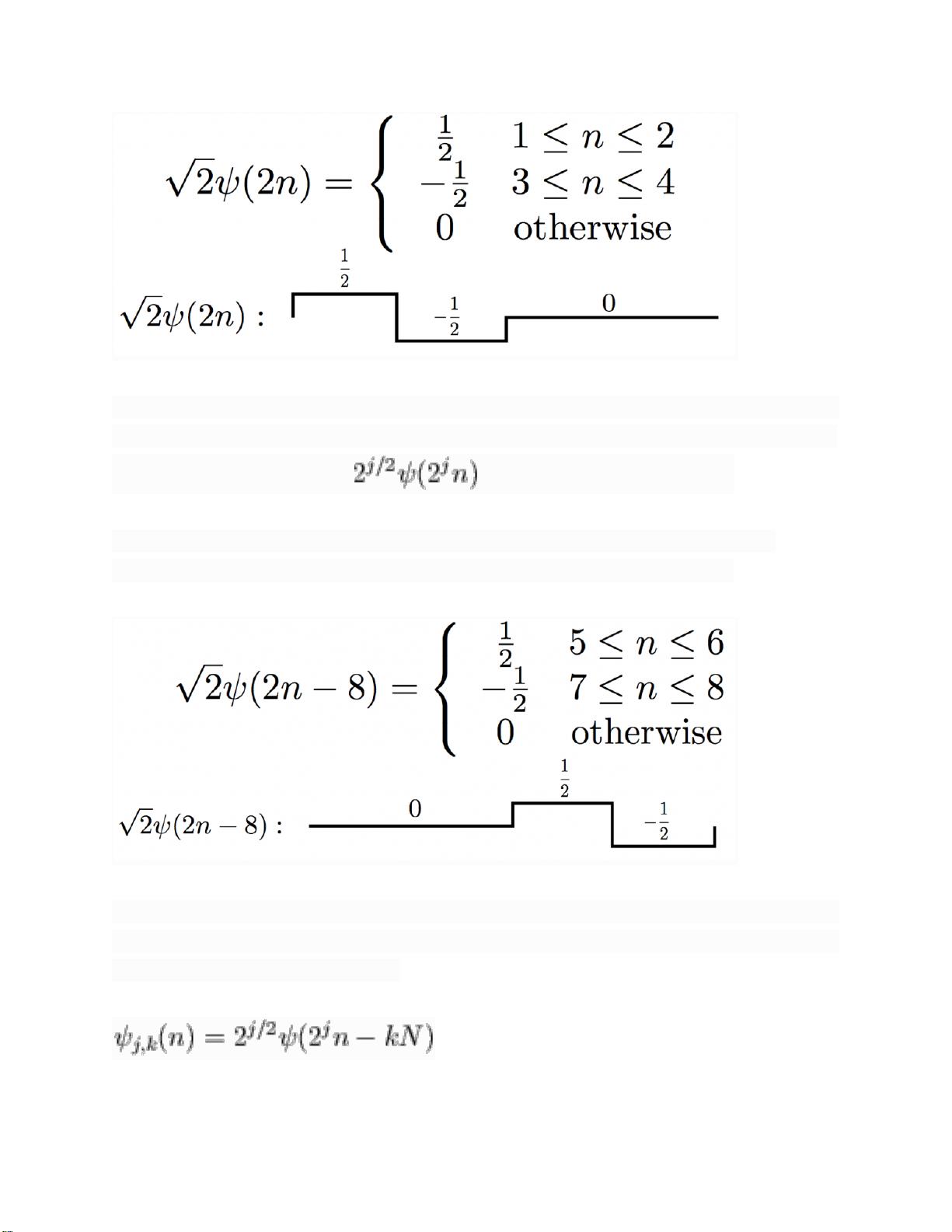
小波变换是一种数学工具,用于分析信号在时间和频率域上的分布,具有良好的时空局部化特性。在小波变换中,母小波和父小波是两个关键概念。母小波是生成小波基的基本函数,而父小波,或称为尺度函数,与母小波一起用于构建小波基。小波基是通过母小波的缩放和平移得到,缩放倍数为2的幂次,平移量与缩放程度有关。
小波级数是小波变换的核心,由一系列正交归一化的小波基组成,能够表示信号在不同尺度和时间位置的信息。这种正交性使得在分解和重构信号时,能有效地减少计算复杂性,并保持信号的能量不变。与傅立叶级数不同,小波级数不仅可以捕获信号的频域特征,还能捕捉到时域细节,实现时间-频率局部化的分析。
小波变换的二维特性意味着它同时在时间轴和频率轴上提供信息。这是因为小波基是通过变化尺度和平移得到的,使得分析能够在不同的分辨率下进行,这就是多解析度分析。多解析度分析允许我们从粗略到精细逐步分析信号,对于处理非平稳信号特别有用。
尺度函数在小波理论中扮演重要角色,它与母小波正交,且自身与其周期平移版本也正交。这种正交性简化了小波分析的数学结构,使得分析更为有效。虽然正交性不是小波变换的必要条件,但在实际应用中,正交小波基更常见,因为它们提供了简洁的表示和高效的算法。
最后,小波变换在运动信号处理中具有广泛的应用,因为它可以揭示信号随时间的变化模式,这对于理解和分析动态过程至关重要。通过深入理解小波变换的原理和特性,无论是理论研究还是工程实践,都能更好地利用这一强大的工具。
总结来说,小波变换是一种强大而灵活的信号分析方法,通过母小波、父小波和正交小波基,实现了信号在时间和频率上的精细分析,尤其适用于处理非平稳信号。多解析度分析则提供了从全局到局部的多尺度视角,使得理解复杂信号成为可能。在实际应用中,掌握小波变换的基础知识对于进行有效的信号处理和分析至关重要。
2019-06-29 上传
2020-07-14 上传
2023-11-16 上传
2022-09-24 上传
2021-05-21 上传
2022-07-14 上传
2022-07-15 上传
2020-10-26 上传
2019-06-25 上传
qq_38577656
- 粉丝: 0
- 资源: 3
最新资源
- 前端协作项目:发布猜图游戏功能与待修复事项
- Spring框架REST服务开发实践指南
- ALU课设实现基础与高级运算功能
- 深入了解STK:C++音频信号处理综合工具套件
- 华中科技大学电信学院软件无线电实验资料汇总
- CGSN数据解析与集成验证工具集:Python和Shell脚本
- Java实现的远程视频会议系统开发教程
- Change-OEM: 用Java修改Windows OEM信息与Logo
- cmnd:文本到远程API的桥接平台开发
- 解决BIOS刷写错误28:PRR.exe的应用与效果
- 深度学习对抗攻击库:adversarial_robustness_toolbox 1.10.0
- Win7系统CP2102驱动下载与安装指南
- 深入理解Java中的函数式编程技巧
- GY-906 MLX90614ESF传感器模块温度采集应用资料
- Adversarial Robustness Toolbox 1.15.1 工具包安装教程
- GNU Radio的供应商中立SDR开发包:gr-sdr介绍