NIPS 2016: David Blei的变分推理教程

需积分: 9 82 浏览量更新于2024-07-18 收藏 24.85MB PDF 举报

"NIPS 2016 Variational Inference Tutorial by David Blei" NIPS (Neural Information Processing Systems) 是一个国际知名的机器学习和计算神经科学会议，每年都会聚集全球顶尖的研究人员和从业者，分享最新的研究成果和技术。2016年的NIPS大会上，David Blei、Rajesh Ranganath和Shakir Mohamed共同进行了一个关于变分推断（Variational Inference）的教程。变分推断是统计学和机器学习领域中的一种重要方法，尤其在处理高维复杂数据时，如主题模型、贝叶斯网络和深度学习模型中。变分推断是一种近似推理技术，用于解决贝叶斯框架下的后验概率计算问题。在实际应用中，我们通常面对的是无法解析求解的后验分布，而变分推断通过寻找一个易于处理的分布家族来逼近这个复杂的后验分布。这种方法通常涉及将目标函数（例如，证据下界ELBO，Evidence Lower Bound）最大化，以找到最接近真实后验的变分分布。在NIPS 2016的这个教程中，他们可能探讨了变分推断的基本原理，包括变分分布的选择、优化算法以及在各种模型中的应用。例如，他们可能提到了Gopalan和Blei在2013年PNAS发表的工作，该工作展示了如何使用变分推断在370万节点的美国专利网络中发现社区结构。此外，变分推断的应用广泛，涵盖了从自然语言处理（NLP）到图像分析的多个领域。例如，它可以用于主题模型（如Latent Dirichlet Allocation, LDA），帮助分析文本数据中的隐藏主题；在游戏分析中，可以理解团队表现和球员影响力；在金融市场预测中，可以估计股票市场动态和投资者行为；在社会科学研究中，可以探索政治派别和选举趋势；在影视行业中，可以预测电影和电视节目的成功；甚至在房地产领域，用于房地产开发和市场趋势的建模。教程可能还涵盖了现代变分推断的方法，比如自动差异化变分推断（Automatic Differentiation Variational Inference, ADVI）、变分自编码器（Variational Autoencoders, VAEs）和黑盒变分推断（Black Box Variational Inference），这些方法大大扩展了变分推断的适用范围，并增强了其在深度学习模型中的应用。通过深入理解变分推断，研究人员和工程师能够更有效地处理不确定性，进行有效的参数估计，并在有限的计算资源下构建复杂的模型。NIPS 2016的这个教程对于希望掌握这一关键工具的AI专业人士来说，无疑是一份宝贵的资源。

History

1006

Carsten Peter son and J ames R . An derson

Coovergence 0 1 eM ColTeia llon Sta

bile

-1 XOR wilh Random

WetgltJ

- 0. 5

' 0 0

1000 10000

t.\ntler

01 SWe8plll

Figure

5: {sf'Bo ut} a nd

out

from th e B M

and

MFT

respec t ively

as fu

nct

ionsof

Nsweep

o For detailson archite ct ure, an nealing sche d ule ,

an d

j values, see figure 3.

Corw

flfOOOC

ll 01

L4e

relallon Oi

llerence

2-4 -1 XOR with Random Welltll l

•

_ _ _

' 0 ' 0 0

1000 10000

tbnber

01 SWeepli

Figure 6 :

as defined in equa tion (3 .17) as a fu n ctio n of N

stKeep

•

For

detai lson architec t u re, a nne ali ng sched ule, and

T ij values, see figure

[Peterson and Anderson 1987]

(a)

(b)

Figure 22: (a) A node S

in a sigmoid belief network machine with its Markov blanket. (b)

The mean ﬁeld equations yield a deterministic relationship, represented in the ﬁgure with

the dotted lines, between the variational parameters µ

and µ

for no des j in the Markov

blanket of node i.

atractablelowerboundontheloglikelihoodandthevariationalparameterξ

can be

optimized along with the other variational parameters.

Saul and Jordan (1998) show that in the limiting case of networks in which each hidden

node has a large number of parents, so that a central limit theorem can be invoked, the

parameter ξ

has a probabilistic interpretation as the approximate exp ectation of σ(z

where σ(·)isagainthelogisticfunction.

For ﬁxed values o f the paramete rs ξ

,bydiﬀerentiating the KL divergence with respect

to the variational parameters µ

,weobtainthefollowingconsistencyequations:

= σ

⎛

⎝

+ θ

(µ

−ξ

⎞

⎠

(67)

where K

is the derivative of −ln

−ξ

+ e

(1−ξ

with respect to µ

.AsSaul,etal.

show, this term depends on node i,itschildj,andtheotherparents(the“co-parents”)of

node j.Giventhattheﬁrsttermisasumovercontributionsfromtheparentsofnodei,

and the second term is a sum over contributions from the children of node i,weseethatthe

consistency equation for a given node again involves contributions from the Markov blanket

of the node (see Fig. 22). Thus, as in the case of the Boltzmann machine, we ﬁnd that the

variational parameters are linked via their Markov blankets and the consistency equation

(Eq. (67)) can be interpreted as a local message-passing algorithm.

Saul, Jaakkola, and Jordan (1996) and Saul and Jordan (1998) also show how to update

the variational parameters ξ

.Thetwopapersutilizetheseparametersinslightlydiﬀerent

ways and obtain diﬀerent update equations. (Yet another related variational approximation

for the sigmoid b elief network, including b oth upper and lower bounds, is presented in

Jaakkola and Jordan, 1996).

Finally, we can compute the gradient with respect to the parameters θ

for ﬁxed vari-

ational parameters µ and ξ.TheresultobtainedbySaulandJordan(1998)takesthe

[Jordan et al. 1999]

Figure 2: The final weights of the network. Each

large block represents one hidden unit. The small

black or white rectangles represent negative or

positive weights with the area of a rectangle rep

resenting the magnitude of the weight. The bot-

tom 12 rows in each block represent the incoming

weights of the hidden unit. The central weight at

the top of each block is the weight from the hidden

unit to the linear output unit. The weight at the

top-right of a block is the bias of the hidden unit.

‘~

-2 2

Figure 3: The final probability distribution that

is used for coding the weights. This distribution

is implemented by adapting the means, variances

and mixing proportions of five gauasians.

is clear that the weights form three fairly sharp clus-

ters. Figure 3 shows that the mixture of 5 Gaussians

has adapted to implement the appropriate coding-prior

for this weight distribution.

The performance of the network can be measured by

comparing the squared error it achievea on the test data

with the error that would be achieved by simply guess-

ing the mean of the correct answera for the test data:

Relative Error =

~c(dc - y.)’

~c(dc - ~)2

(27)

We ran the optimization five times using different ran-

domly chosen valuea for the initial means of the noisy

weights. For the network that achieved the lowest value

of the overall cost function, the relative error was 0.286.

This compares with a relative error of 0.967 for the same

network when we used noise-free weights and did not

penalize their information content. The best relative

error obtained using simple weight-decay with four non-

linear hidden units was .317. This required a carefully

chosen penalty coefficient for the squared weights that

corresponds to uf/a~ in equation 4. To set this weight-

decay coefficient appropriately it was necessary to try

many different values on a portion of the training set

and to use the remainder of the training set to decide

which coefficient gave the best generalization. Once the

beat coefficient had been determined the whole of the

training set was used with this coefficient. A lower er-

ror of 0.291 can be achieved using weight-decay if we

gradually increase the weight-decay coefficient and pick

the value that gives optimal performance on the test

data. But this is cheating. Linear regression gave a

huge relative error of 35.6 (gross overfitting) but this

fell to 0.291 when we penalized the sum of the squarea

of the regression coefficients by an amount that was ch~

sen to optimize performance on the test data. This is

almost identical to the performance with 4 hidden units

and optimal weight-decay probably because, with small

weights, the hidden units operate in their central linear

range, so the whole network is effectively linear.

[Hinton and van Camp 1993]



Variational inference adapts ideas from statistical physics to probabilistic

inference. Arguably, it began in the late eighties with Peterson and

Anderson (1987), who used mean-ﬁeld methods to ﬁt a neural network.



This idea was picked up by Jordan’s lab in the early 1990s—Tommi

Jaakkola, Lawrence Saul, Zoubin Gharamani—who generalized it to

many probabilistic models. (A review paper is Jordan et al., 1999.)



In parallel, Hinton and Van Camp (1993) also developed mean-ﬁeld for

neural networks. Neal and Hinton (1993) connected this idea to the EM

algorithm, which lead to further variational methods for mixtures of

experts (Waterhouse et al., 1996) and HMMs (MacKay, 1997).

Today

(a) Learned Frey Face manifold (b) Learned MNIST manifold

Figure 4: Visualisations of learned data manifold for generative models with two-dimensional latent

space, learned with AEVB. Since the prior of the latent space is Gaussian, linearly spaced coor-

dinates on the unit square were transformed through the inverse CDF of the Gaussian to produce

values of the latent variables z. For each of these values z, we plotted the corresponding generative

✓

(x|z) with the learned parameters ✓.

(a) 2-D latent space (b) 5-D latent space (c) 10-D latent space (d) 20-D latent space

Figure 5: Random samples from learned generative models of MNIST for different dimensionalities

of latent space.

B Solution of D



(z)||p

✓

(z)), Gaussian case

The variational lower bound (the objective to be maximized) contains a KL term that can often be

integrated analytically. Here we give the solution when both the prior p

✓

(z)=N(0, I) and the

posterior approximation q



(z|x

(i)

) are Gaussian. Let J be the dimensionality of z. Let µ and 

denote the variational mean and s.d. evaluated at datapoint i, and let µ

and 

simply denote the

j-th element of these vectors. Then:

✓

(z) log p(z) dz =

N(z; µ, 

) log N(z; 0, I) dz

= 

log(2⇡) 

j=1

(µ

+ 

)

Stochastic Back-propagation in DLGMs

(a) NORB (b) CIFAR (c) Frey

Figure 4. a) Performance on the NORB dataset. Left: S a mp l es from the training data. Right: sampled pixel means from

the model. b) Performance on CIFAR10 patches. Left: Samples from the training data. Right: Sampled pixel means

from the model. c) Frey faces data. Left: data samples. Right: model samples.

Figure 5. Imputation results on MNIST digits. The ﬁrst

column shows the true data. Column 2 shows pixel loca-

tions set as missing in grey. The remaining columns show

imputations a n d denoising of the i ma g es for 15 iterations,

starting left to right. Top: 60% missingness. Middle: 80%

missingness. Bottom: 5x5 patch missing.

matics and experimental design. We show the ability

of the model to impute missing data using the MNIST

data set in ﬁgure 5. We test the imputation ability

under two di↵erent missingness types (Little & Rubin,

1987): Missing-at-random (MAR), where we consider

60% and 80% of the pixels to be missing randomly, and

Not Missing-at-random (NMAR), where we consider a

square region of the image to be missing. The model

produces very good completions in both test cases.

There is uncertainty in the identity of the image. This

is expected and reﬂected in the errors in these comple-

tions as the resampling procedure is run, and furth er

demonstrates the ability of the model to capture the

diversity of the und er l yi n g data. We do not integrate

over the missing values in our imputation procedure,

but use a procedure that simulates a Markov chain

that we show converges to the true marginal distribu-

tion. The procedure to sample from the missing pixels

given the observed pixels is explained in appendix E.

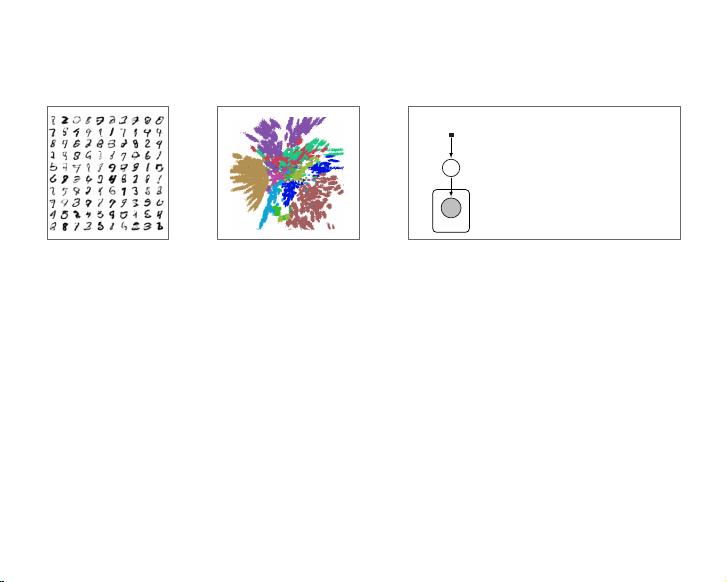
Figure 6. Two dimensional embedding of the MNIST data

set. Each colour correspo n d s to one of the digit classes.

6.5. Data Visualisation

Latent variable models such as DLGMs are often used

for visualisation of high-dimensional data sets. We

project the MNIST data set to a 2-dimensional latent

space and use this 2-D embedding as a visualisation of

the data. A 2-dimensional embedding of the MNIST

data set is shown in ﬁgure 6. The classes separate

into di↵erent regions indicating that such a tool can

be useful in gaining insight into the structure of high-

dimensional data sets.

7. Discussion

Our algorithm generalises to a large class of models

with continuous latent variables, which include Gaus-

sian, non-negative or sparsity-promoting latent vari-

ables. For models with discrete latent variables (e.g.,

sigmoid belief networks), policy-gradient approaches

that improve upon the REINFORCE approach remain

the most general, but intelligent design is needed to

control t h e gradient-variance in high dimensional set-

tings.

These models are typically used with a large number

[Kingma and Welling 2013] [Rezende et al. 2014]

✓

˛ D 1:5;  D 1

data {

int N; // number of observations

int x[N]; // discrete - valued observations

}

parameters {

// latent variable , must be positive

real < lower=0> th eta ;

}

model {

// non - conjugate prior for latent variable

theta ~ weibul l (1.5 , 1) ;

// likelihood

for (n in 1:N)

x[n] ~ poisson(theta);

}

Figure 2: Specifying a simple nonconjugate probability model in Stan.

analysis posits a prior density p.✓/ on the latent variables. Combining the likelihood with the prior

gives the joint density p.X; ✓/ D p.X j ✓/p.✓/.

We focus on approximate inference for diﬀerentiable probability models. These models have contin-

uous latent variables ✓. They also have a gradient of the log-joint with respect to the latent variables

✓

logp.X; ✓/. The gradient is valid within the support of the prior supp.p.✓ // D

✓ j ✓ 2

and p.✓/>0

✓ R

, where K is the dimension of the latent variable space. This support set

is important: it determines the support of the posterior density and plays a key role later in the paper.

We make no assumptions about conjugacy, either full or conditional.

For example, consider a model that contains a Poisson likelihood with unknown rate, p.x j ✓ /. The

observed variable x is discrete; the latent rate ✓ is continuous and positive. Place a Weibull prior

on ✓, deﬁned over the positive real numbers. The resulting joint density describes a nonconjugate

diﬀerentiable probability model. (SeeFigure 2.) Its partial derivative@=@✓ p.x; ✓ / is valid within the

support of the Weibull distribution, supp.p.✓ // D R

⇢ R. Because this model is nonconjugate, the

posterior is not a Weibull distribution. This presents a challenge for classical variational inference.

In Section 2.3, we will see how  handles this model.

Manymachinelearning models are diﬀerentiable. Forexample: linear and logisticregression, matrix

factorization with continuous or discrete measurements, linear dynamical systems, and Gaussian pro-

cesses. Mixture models, hidden Markov models, and topic models have discrete random variables.

Marginalizing out these discrete variables renders these models diﬀerentiable. (We show an example

in Section 3.3.) However, marginalization is not tractable for all models, such as the Ising model,

sigmoid belief networks, and (untruncated) Bayesian nonparametric models.

2.2 Variational Inference

Bayesian inference requires the posterior density p.✓ j X/, which describes how the latent variables

vary when conditioned on a set of obser vations X. Many posterior densities are intractable because

their normalization constants lack closed forms. Thus, we seek to approximate the posterior.

Consider an approximating density q.✓ I / parameterized by . We make no assumptions about its

shape or support. We want to ﬁnd the parameters of q.✓ I / to best match the posterior according to

some loss function. Variational inference () minimizes the Kullback-Leibler () divergence from

the approximation to the posterior [2],



⇤

D argmin



q.✓ I / k p.✓ j X/

: (1)

Typically the  divergencealso lacks a closed form. Instead we maximize the evidence lower bound

(), a proxy to the  divergence,

L./ D E

q.✓/

⇥

logp.X; ✓/

⇤

E

q.✓/

⇥

logq.✓ I /

⇤

The ﬁrst term is an expectation of the joint density under the approximation, and the second is the

entropy of the variational density. Maximizing the  minimizes the  divergence [1, 16].

The posterior of a fully conjugate model is in the same family as the prior; a conditionally conjugate model

has this property within the complete conditionals of the model [3].

[Kucukelbir et al. 2015]



There is now a ﬂurry of new work on variational inference, making it

scalable, easier to derive, faster, more accurate, and applying it to more

complicated models and applications.



Modern VI touches many important areas: probabilistic programming,

reinforcement learning, neural networks, convex optimization, Bayesian

statistics, and myriad applications.



Our goal today is to teach you the basics, explain some of the newer ideas,

and to suggest open areas of new research.

剩余161页未读，继续阅读

YongXien

粉丝: 0
资源: 1

NIPS 2016: David Blei的变分推理教程

NIPS 2016 Tutorial: Generative Adversarial Networks , by Ian Goodfellow

NIPS-tutorial-2016 非常不错的介绍

2016_NIPS_VI_tutorial

Deep Learning: Practice and Trends [NIPS2017 Tutorial]

Deep Learning for Computer Vision NIPS 2013 Tutorial slide by Rob Fergus

SVM and Kernel method (nips tutorial)

schapire-NIPS-07-tutorial.pdf

DL-Tutorial-NIPS2015

Yann Le Cun 在nips2016上Predictive Learning 的tutorial演讲ppt

DeepMind Nips 2016

最新资源

Deep Learning  for Computer Vision NIPS 2013 Tutorial slide by Rob Fergus