复分析入门:Michael E. Taylor的数学研究生教程
下载需积分: 16 | PDF格式 | 2.92MB |
更新于2024-06-28
| 111 浏览量 | 举报
"《Introduction to Complex Analysis》是Michael E. Taylor撰写的一本研究生层次的复分析教材,属于美国数学学会的研究生数学系列(GSM202)。这本书旨在引导读者理解并掌握复变函数的基本概念和性质,包括复数、复函数、复积分及其在微积分中的应用。"
复分析是数学的一个重要分支,主要研究复数作为变量的函数。在本书中,Michael E. Taylor将介绍一系列与复数相关的基础函数,如幂次和分数幂、指数和对数、三角函数及其逆函数,以及读者可能会遇到的许多新函数。这些函数不仅在复数域内定义,而且自然地扩展了实数域内的概念。
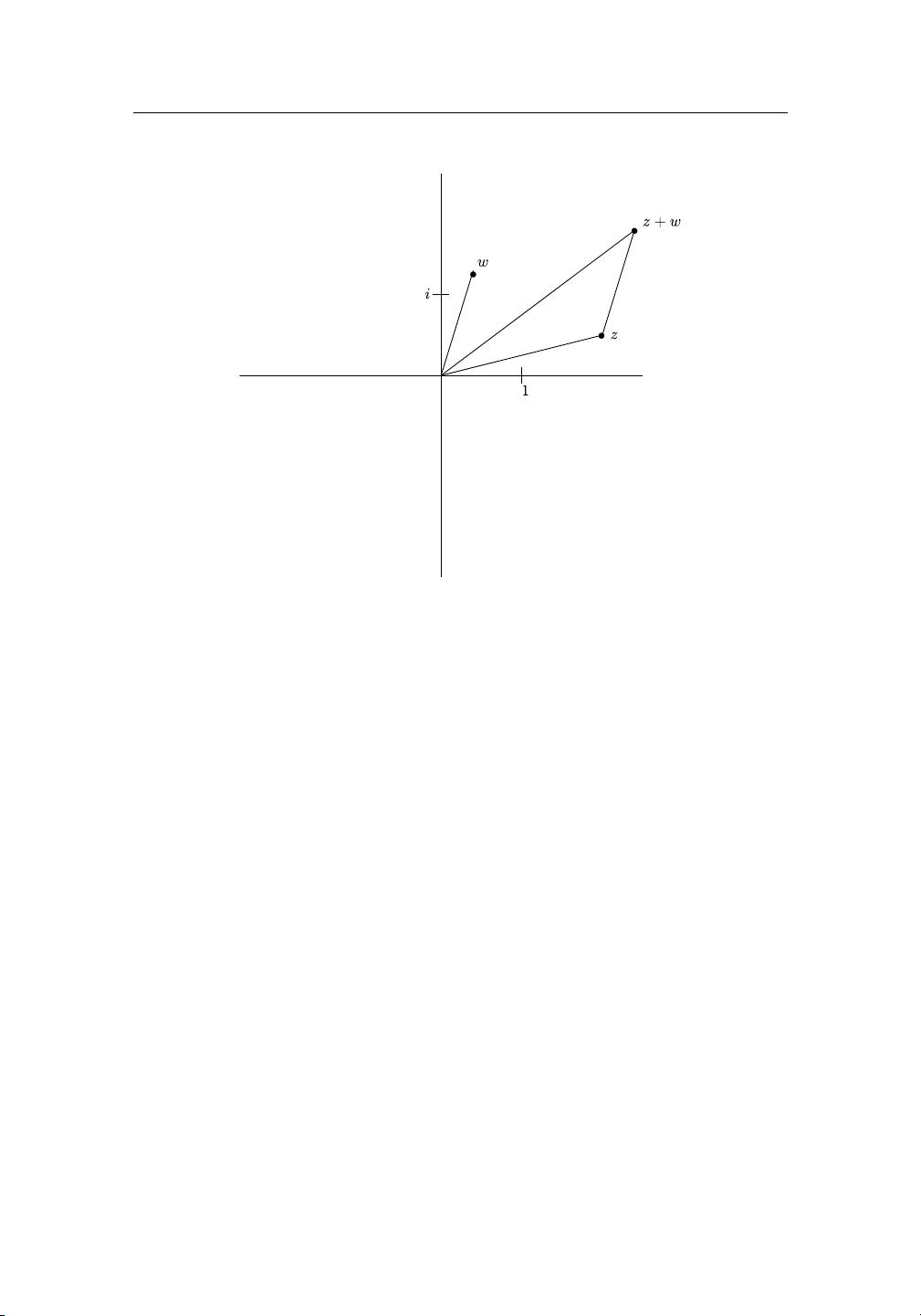
复数是由实部和虚部组成的数,它们的形式为a + bi,其中a和b是实数,i是虚数单位,满足i² = -1。复分析研究这些复数如何作为自变量影响函数的行为,揭示了复数在物理和工程领域中广泛的应用,例如振动理论、电磁学和量子力学。
书中会涵盖复数的基本运算,如加法、减法、乘法和除法,并且会深入讨论复函数,如幂函数z^n(其中z是复数,n是实数或复数)、指数函数e^z和对数函数log z。这些函数的复数扩展具有独特的几何意义,例如,幂函数在复平面上形成了分形图案,而复指数函数是周期性的,这使得它在傅里叶分析中有重要作用。
复分析的核心概念之一是复导数,它扩展了实数上的导数概念,提供了分析函数在复平面上局部线性近似的方法。Taylor还会讨论Cauchy-Riemann方程,这是确定一个函数是否在复平面上可微的必要条件。此外,复积分——包括Cauchy积分公式和留数定理——对于理解复函数的性质和求解实数问题至关重要,比如计算实函数的实积分。
复分析也包含了复分析中的重要定理,如Liouville定理(关于全纯函数的有界性和常数性)和最大模原理(指出在闭区域上解析函数的最大模必须在边界上取得)。这些定理对于理解复函数的整体行为至关重要。
《Introduction to Complex Analysis》是一本全面介绍复变函数理论的教材,适合对复数理论和应用感兴趣的研究生或高级本科生学习。通过阅读本书,读者可以系统地学习复数理论,掌握复分析的基本工具,并能够解决实际问题。书后还附有参考文献和索引,方便读者进一步探索相关主题。
相关推荐




wxwpxh
- 粉丝: 16
最新资源
- ASP.NET集成支付宝即时到账支付流程详解
- C++递推法在解决三道经典算法问题中的应用
- Qt_MARCHING_CUBES算法在面绘制中的应用
- 传感器原理与应用课程习题解答指南
- 乐高FLL2017-2018任务挑战解析:饮水思源
- Jquery Ui婚礼祝福特效:经典30款小型设计
- 紧急定位伴侣:蓝光文字的位置追踪功能
- MATLAB神经网络实用案例分析大全
- Masm611: 安全高效的汇编语言调试工具
- 3DCurator:彩色木雕CT数据的3D可视化解决方案
- 聊天留言网站开发项目全套资源下载
- 触摸屏适用的左右循环拖动展示技术
- 新型不连续导电模式V_2控制Buck变换器研究分析
- 用户自定义JavaScript脚本集合分享
- 易语言实现非主流方式获取网关IP源码教程
- 微信跳一跳小程序前端源码解析