R语言实例：自相关问题与一阶差分法解决

该资源是一个关于R语言处理自相关问题的实例分析，包含了R代码和数据分析，主要讨论了自相关性在统计建模中的影响以及如何检测和解决自相关问题。 在统计建模，尤其是线性回归分析中，自相关问题是一个重要的考虑因素。自相关是指一个时间序列中的误差项（残差）并非独立，它们之间存在一定的关联性。对于线性回归模型，理想的假设是误差项相互独立，但实际应用中，这种假设往往不成立。自相关可能是由经济时间序列的内在特性（如惯性或延缓性）、模型适应性不足或者数据生成过程中的其他因素导致的。 自相关的存在会带来一系列后果： 1. 参数估计量虽然无偏且一致，但不再是最佳线性无偏估计量（BLUE），这意味着它们的效率降低。 2. OLS（普通最小二乘法）估计量的方差被低估，影响了模型的精度。 3. 基于这些估计量的统计检验（如t检验和F检验）不再可靠，可能导致错误的变量显著性判断。 4. 用这样的模型进行预测时，预测效果可能会大大减弱。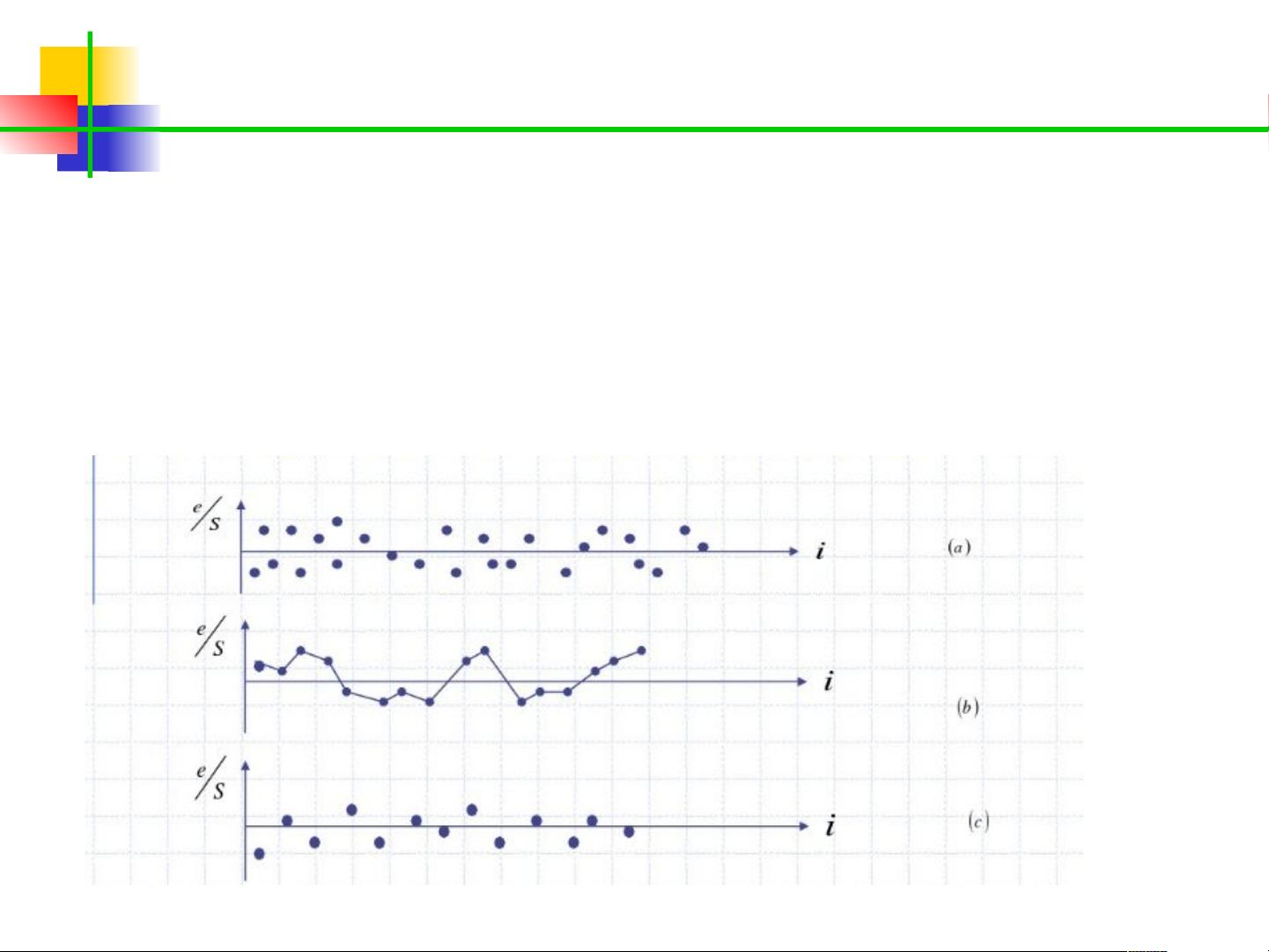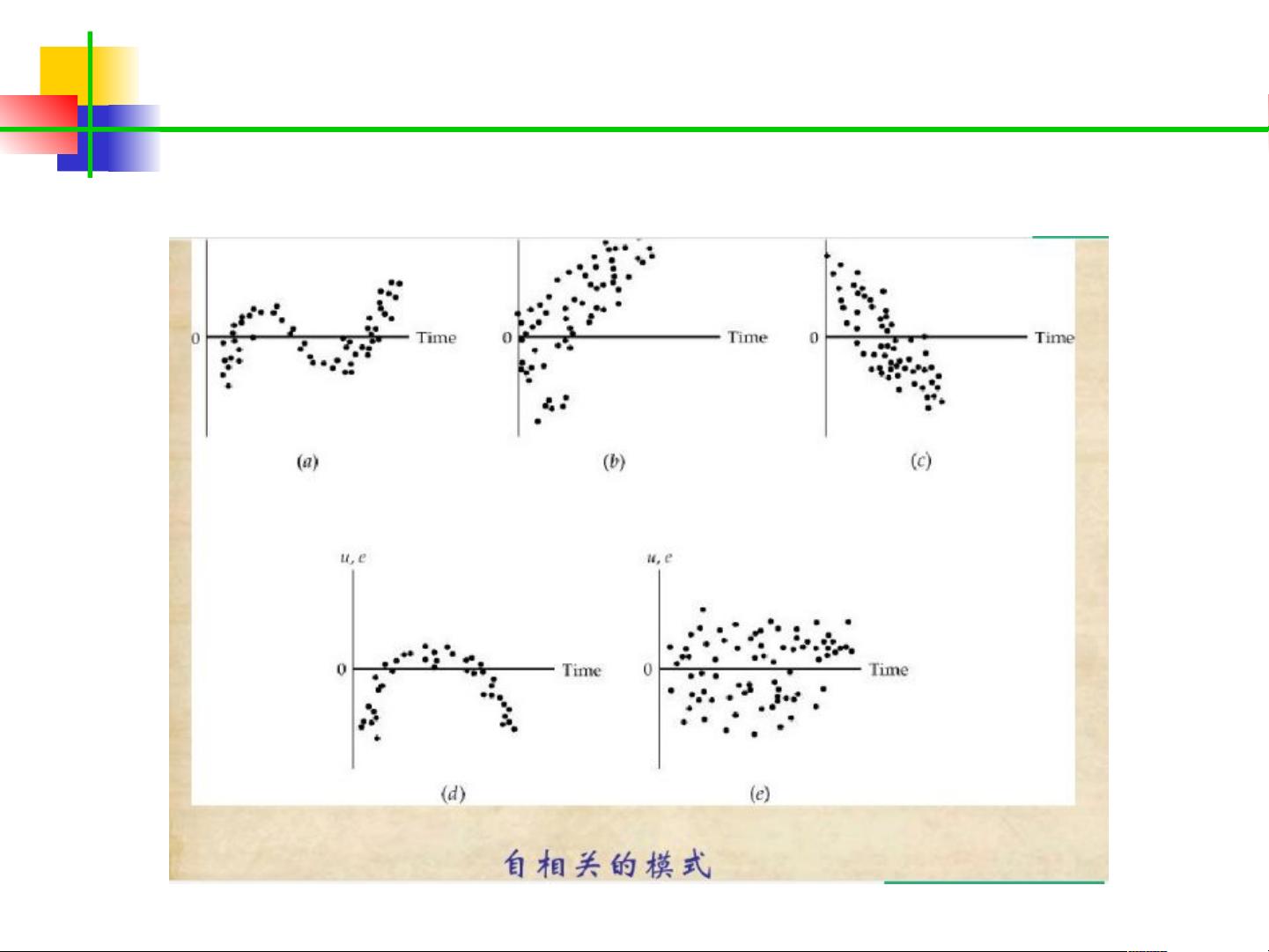 为了检测自相关，我们可以采用残差序列图进行分析，如果残差呈现出锯齿形或循环模式，可能表明存在自相关。此外，Durbin-Watson（D-W）检验是一种常用的统计检验方法，其统计量可以用来判断是否存在自相关。在R语言中，可以使用`lmtest`包的`dwtest`函数进行D-W检验。 例如，文档中提到的美国商业部门真实工资与生产率的关系分析，通过对数据进行线性回归并计算D-W统计量，可以发现残差存在正的自相关。进一步的解决方法是采取一阶差分法，通过对因变量和解释变量求差分来消除自相关。这种方法会改变模型的形式，通常不再包含截距项。 在R代码示例中，使用`diff()`函数进行一阶差分，然后对差分后的数据进行新的线性回归（`lm.reg2`），这有助于改善模型的估计和预测性能。 理解和处理自相关是R语言数据分析中的关键技能，它涉及到模型的正确设定、参数估计的有效性和预测的准确性。通过识别和应用适当的修正方法，如一阶差分法，可以提高统计建模的质量和可靠性。