线性代数几何意义探索：从向量到行列式

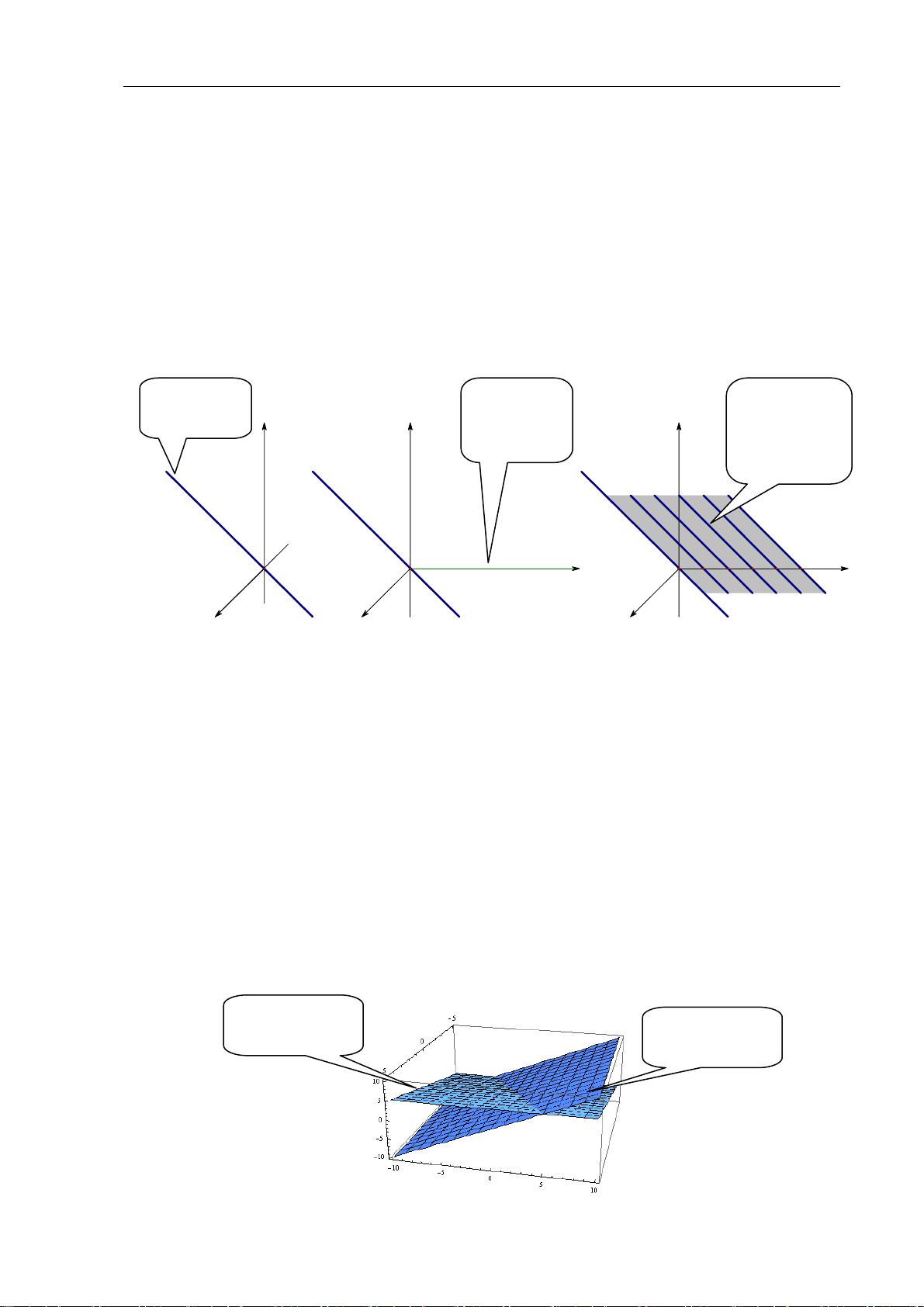
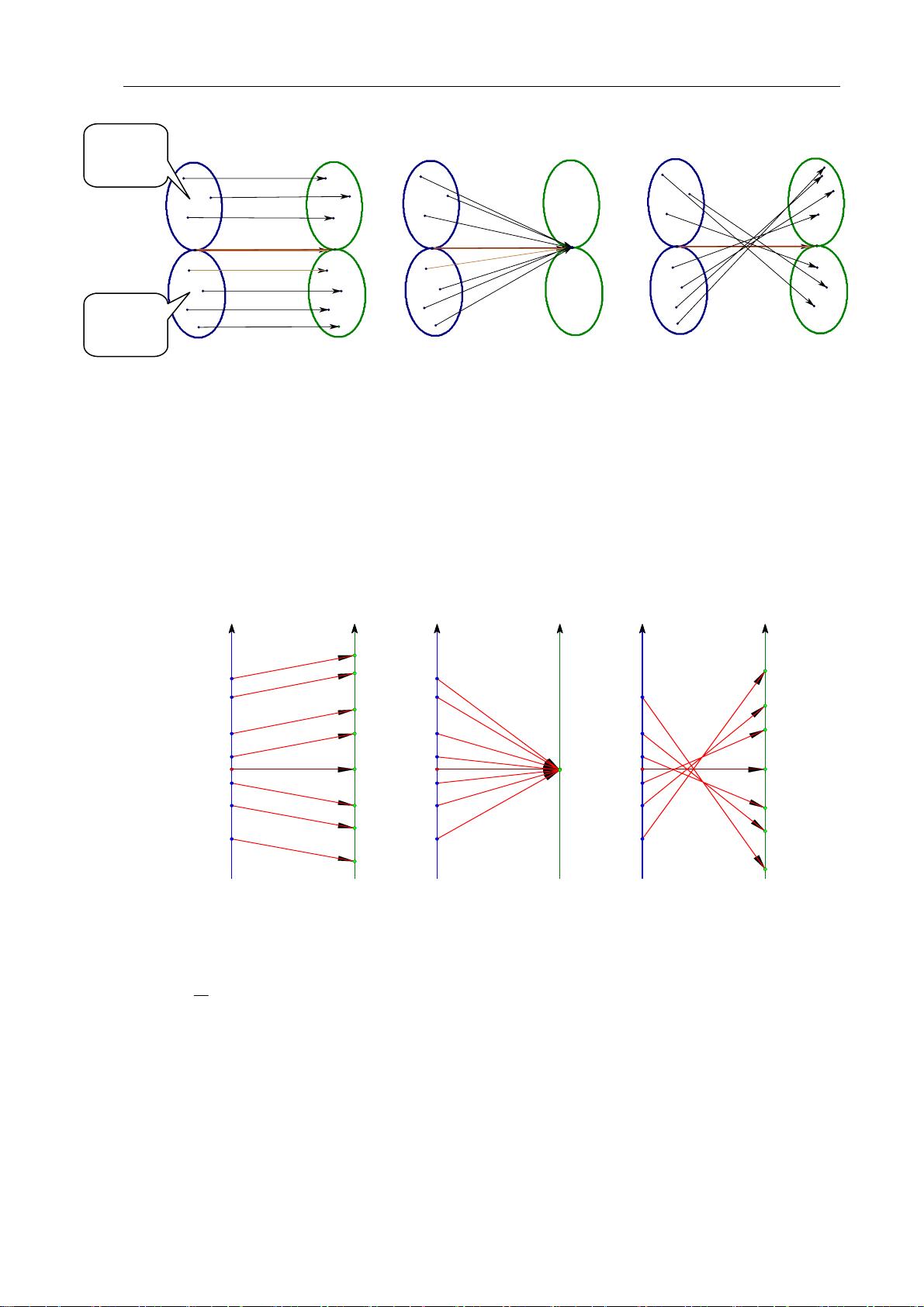
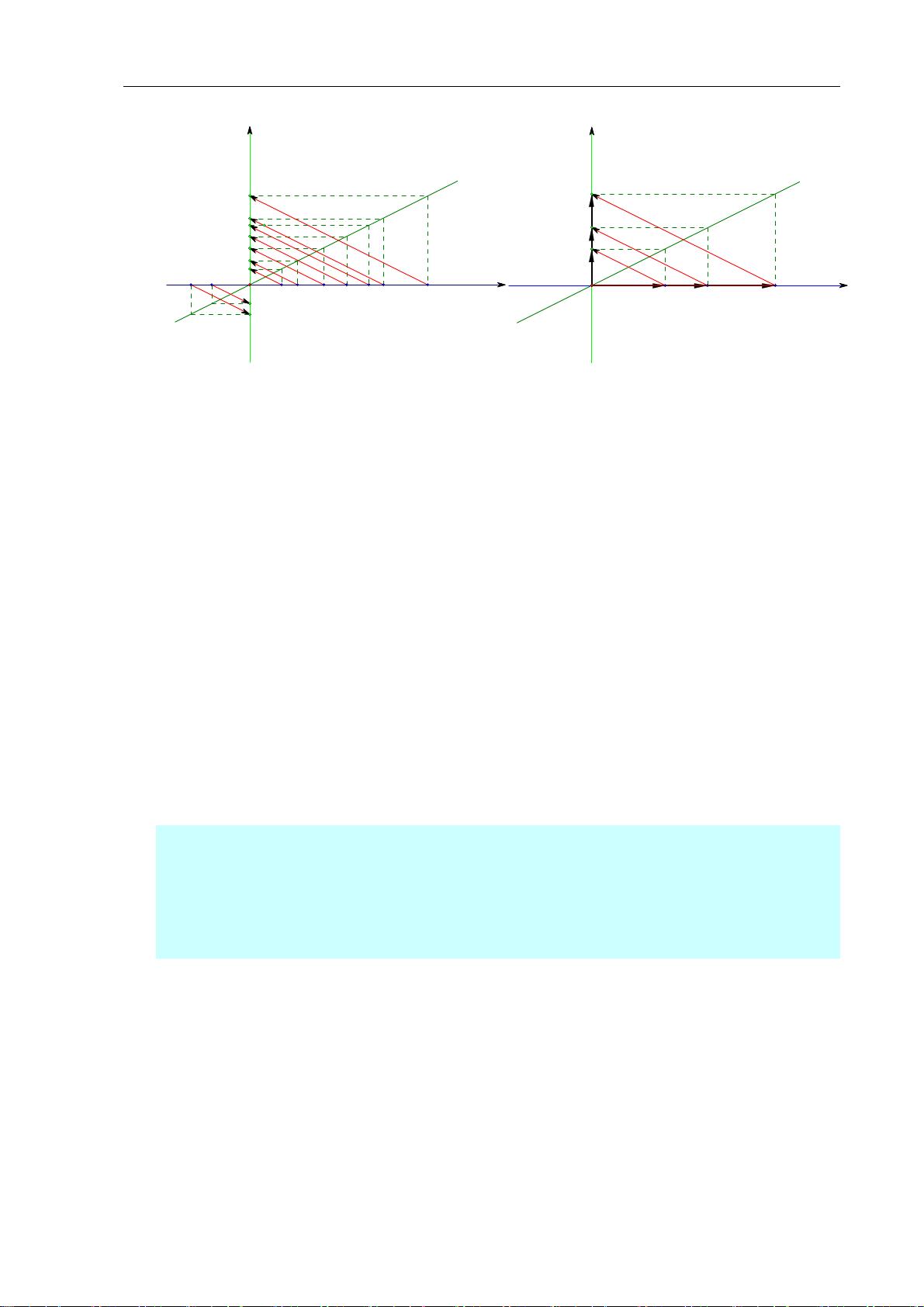
"该资源是一本关于线性代数几何意义的教材，涵盖了从线性代数的基础概念到向量和行列式的几何解释，旨在帮助读者深入理解抽象数学概念的实际应用。" 线性代数是现代数学的一个核心分支，它在几何学、物理学、工程学等领域都有广泛的应用。在《线性代数的几何意义1-5》中，作者通过几何直观的方式解释了线性代数的基本概念，使得这个主题更加易懂。 首先，书中的"为什么要给出线性代数的几何意义"部分强调了几何理解对于掌握线性代数的重要性。线性代数不仅涉及抽象的矩阵和向量运算，更是一种描述现实世界中线性关系的有效工具。通过几何直观，我们可以更好地理解这些抽象概念，并将它们应用于实际问题。 在第一章中，作者介绍了线性代数的基础，包括"代数"和"线性"的含义。线性函数是基本的线性结构，其在多维空间中的扩展，如多元线性函数，具有直观的几何意义，比如在二维或三维空间中表示直线和平面。线性映射和线性变换则揭示了空间结构如何在变换下保持不变，这对于理解和研究几何对象的性质至关重要。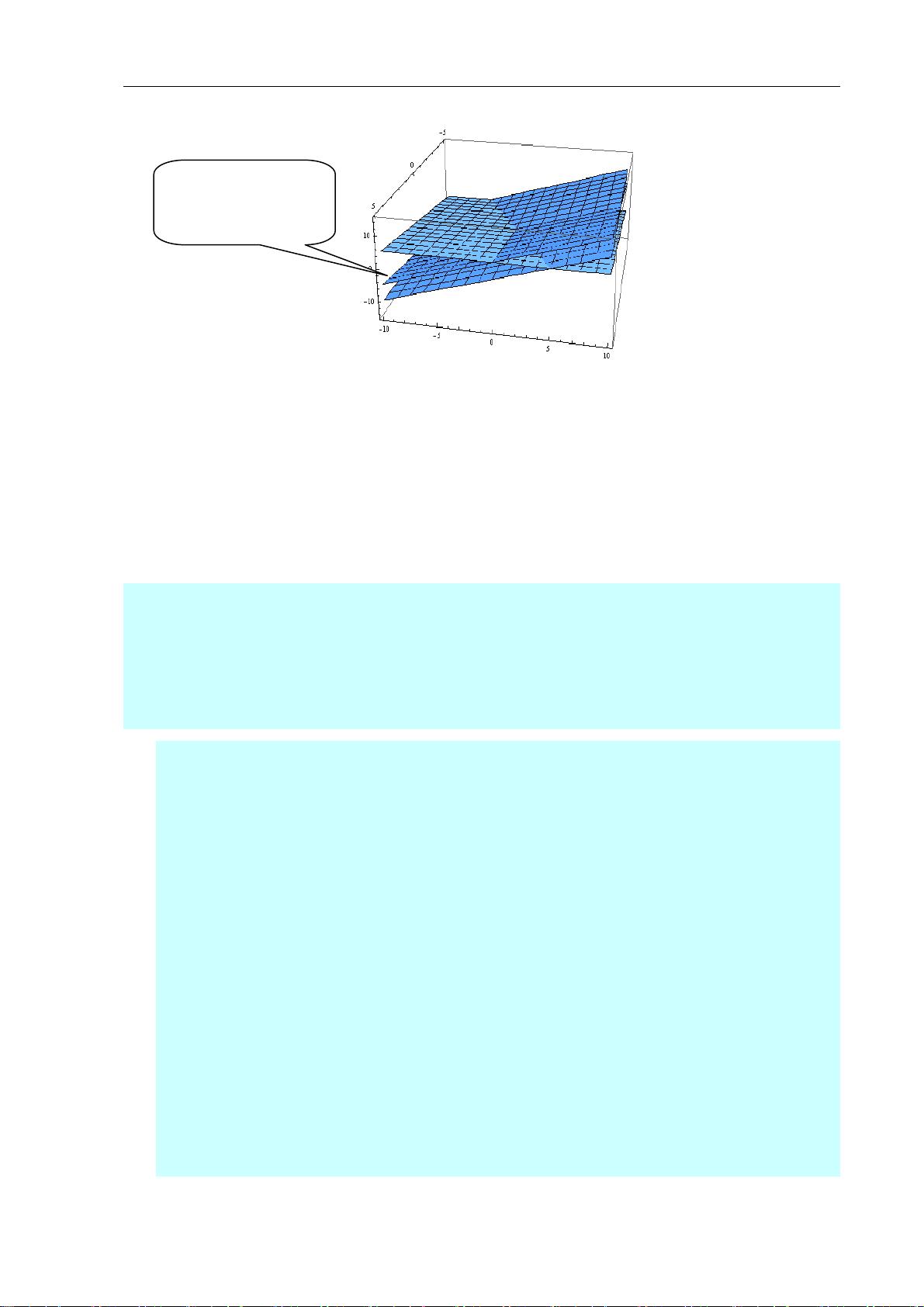 第二章详细探讨了向量的几何意义。向量不仅是代数运算的对象，也是表示方向和大小的实体。向量的加法、内积和叉积都与几何操作（如平行移动、长度和角度）以及物理现象（如力的作用）紧密关联。向量的混合运算，如分配律和结合律，也有清晰的几何解释。此外，书中还讨论了向量除法、变向量、复向量以及向量与微积分和解析几何的联系，这些都是理解向量在更复杂问题中作用的关键。 第三章聚焦于行列式的几何意义，行列式是线性代数中的一个关键工具，它可以用来判断方程组的解的情况或者确定一个变换是否保持面积或体积不变。二阶和三阶行列式的几何解释有助于理解它们如何反映了平面和空间中的面积和体积。行列式的对角化过程和乘积项的几何意义进一步加深了对线性变换几何效果的理解。 《线性代数的几何意义1-5》是一本深入浅出的教材，通过丰富的几何图像和实例，帮助读者建立对线性代数概念的直观理解，从而提升学习效率和应用能力。无论是初学者还是需要复习的读者，都能从中受益。