"MHT算法及其在多传感器跟踪中的问题研究"
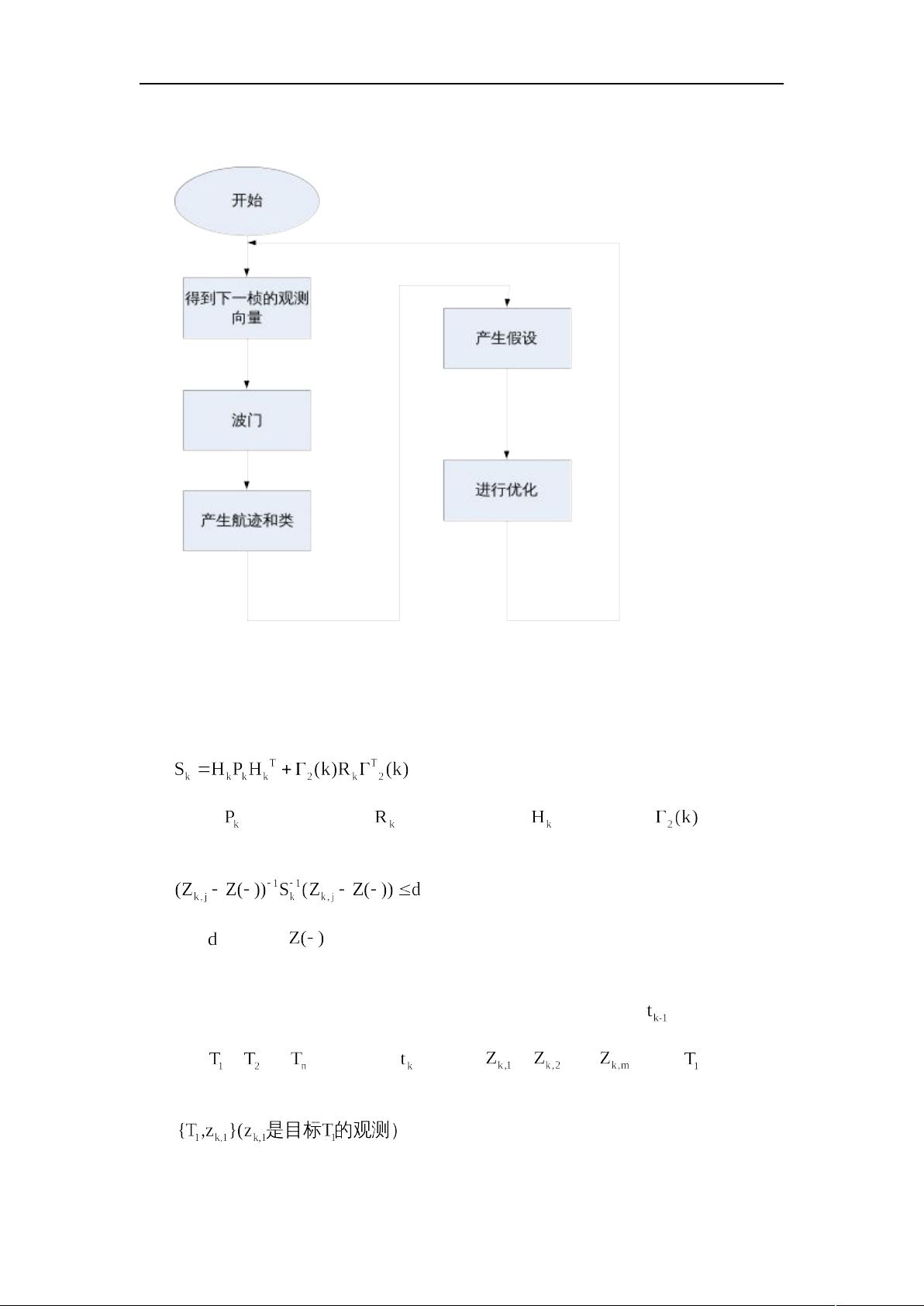
MHT算法(Multiple Hypothesis Tracking)是一种用于多传感器跟踪的逻辑算法。在数据关联发生冲突时,MHT算法通过形成多种假设来延迟做出决策。相比于PDA算法(Probabilistic Data Association),MHT算法不会将假设进行加权平均,而是保留多个假设并在之后的观测中解决不确定性。
在MHT算法中,关键术语和技术起着重要的作用。由于数据关联需要保留所有可能的假设,因此MHT算法的计算量会非常大,涉及到大量的轨迹和假设。为了保证计算的可行性,需要采用一些技术手段,如聚类、假设和轨迹的剪枝(N-scan pruning)以及轨迹的合并(track merging)等。
聚类在MHT算法中起到了关键的作用。通过对观测数据进行聚类,可以将相似的数据点分组,从而降低计算的复杂度。聚类可以用于减少轨迹数量,在跟踪过程中将轨迹进行分组,只保留最有可能的轨迹。这样一来,可以降低计算量,并且保留了重要的轨迹信息。
另一个关键技术是假设和轨迹的剪枝。在MHT算法中,假设和轨迹的数量会呈指数级增长,为了保证计算的可行性,需要通过剪枝来减少不必要的假设和轨迹。一种常用的剪枝方法是N-scan pruning,即通过限制假设和轨迹的扫描次数来减少计算量。只有具有足够的证据和可靠性的假设才继续进行跟踪,而不可靠的假设则会被剪枝掉。
此外,轨迹的合并也是MHT算法中的重要技术之一。在多个传感器跟踪的过程中,可能存在多个相似的轨迹,通过将这些相似的轨迹合并为一个更可靠的轨迹,可以提高跟踪的准确性和可靠性。
总结来说,MHT算法是一种逻辑算法,用于在多个传感器跟踪中处理数据关联的冲突。通过形成多种假设和延迟决策,MHT算法能够解决当前扫描帧的不确定性问题。为了保证计算的可行性,MHT算法使用聚类、假设和轨迹的剪枝以及轨迹的合并等关键技术。这些技术能够降低计算复杂度,提高跟踪的准确性和可靠性。虽然MHT算法的计算量较大,但是通过合理的技术应用,可以使该算法在多传感器跟踪中发挥重要作用。
2644 浏览量
点击了解资源详情
点击了解资源详情
2024-11-03 上传
2021-03-17 上传
256 浏览量
点击了解资源详情
zjy19890921
- 粉丝: 1
最新资源
- Java开发手册:高清中文版及详细目录解析
- Gulp命名模块:简化前端未命名Require模块管理
- JavaScript实现经典贪吃蛇游戏教程
- 在线考试系统2.7.7版本全面升级,功能更强大
- STM32F303基础工程文件详解
- 江南红月游戏服务器端及GM工具源码发布
- FFXIV开瓶器制作指南与在线应用介绍
- Azure API管理动手实验室:研讨会指南
- jeecg-boot 2.1实现在线表单与Vue路由页面集成
- API测试示例实践:深入解析HTML应用
- pwatools: 快速构建跨平台PWA的JavaScript库
- IPL数据集探索性数据分析深度解读
- 构建.NET Core MVC与EF Core集成Demo
- Android应用实现滑动刷新功能的示例教程
- VCE文件打开工具v3.1注册版安装与使用教程
- Fullstaq Ruby Server Edition:高效内存管理与快速安装的Ruby发行版