赵磊讲解：线段树入门教程——区间操作与应用

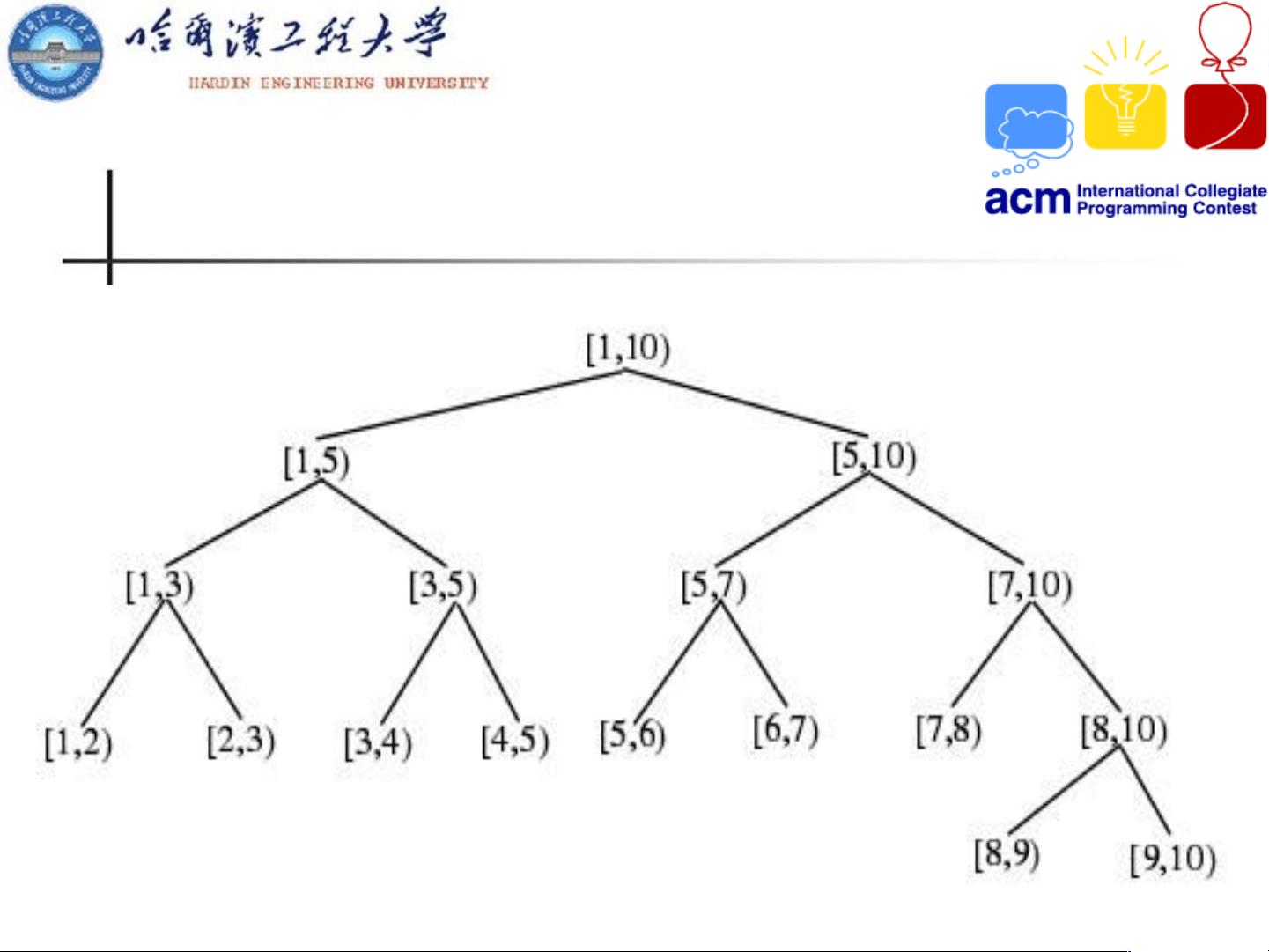
线段树是一种高效的数据结构，用于解决区间相关的查询问题，特别是在需要频繁进行区间更新和查找操作的场景下，如动态维护区间最值、求区间和等。讲课人赵磊通过ACM东北组委会制作的PPT，向初学者介绍了线段树的基础概念和特性。 首先，线段树并非普通的二叉树，而是将区间问题抽象为树状结构。每个节点代表一个区间，而非单个元素，例如节点[left, right)代表的是区间[l, r)。这个结构使得每个非叶节点的两个子节点代表的是半区间的并集，方便处理区间内的聚合操作。例如，对于节点[left, mid)和[mid, right)，它们合并后表示的是[l, r)整个区间。 线段树的一个重要特性是其高度为logN，这意味着查询复杂度可以达到对数级别，相比于线性搜索或直接遍历区间，大大提高了效率。线段树还支持快速地将任意长度为L的区间分解为不超过2logL个子区间，这样可以减少重复计算，确保高效处理大量区间操作。 节点的存储方式很重要，通常采用数组或者链表实现。每个节点包含两个字段，left和right，分别表示该节点所代表的区间范围。在实际应用中，节点结构可能会根据需求进行优化，如引入lazy propagation（懒惰化）技术来处理某些更新操作。 举例来说，题目中的绳子染色问题，ZLGG想要知道最后染色的部分长度，通过线段树可以在O(logN)的时间复杂度内解决，而直接朴素方法可能会因为数据范围过大导致超时。 线段树的另一个关键优势是可以表示任何区间，这使得它可以应用于多种区间查询场景。例如，当需要计算多个区间并集、查询区间最大值或最小值，以及支持区间插入、删除和修改等操作时，线段树都是理想的选择。 线段树是一种强大的工具，通过其高效的区间处理能力和灵活的结构设计，适用于各种需要高效区间查询和更新的问题。掌握线段树，不仅有助于提高编程竞赛解题效率，也是数据结构和算法学习的重要一环。